由來
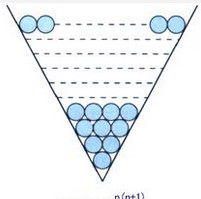
三角形數傳說古希臘畢達哥拉斯(約公元前570-約公元前500年)學派的數學家經常在沙灘上研究數學問題,他們在沙灘上畫點或用小石子來表示數。比如,他們研究過由於這些數可以用如右圖所示的三角形點陣表示,他們就將其稱為三角形數。
 數列
數列正方形數
類似地,被稱為正方形數,因為這些數能夠表示成正方形。
因此,按照一定順序排列的一列數成為數列。
數列定義
按一定次序排列的一列數稱為數列(sequenceofnumber)。數列中的每一個數都叫做這個數列的項。排在第一位的數稱為這個數列的第1項(通常也叫做首項),排在第二位的數稱為這個數列的第2項……排在第n位的數稱為這個數列的第n項。概念
數列的一般形式可以寫成a1,a2,a3,…,an,…
簡記為{an},項數有限的數列為“有窮數列”(finitesequence),項數無限的數列為“無窮數列”(infinitesequence)。
從第2項起,每一項都大於它的前一項的數列叫做遞增數列;如:1,2,3,4,5,6,7
從第2項起,每一項都小於它的前一項的數列叫做遞減數列;如:8,7,6,5,4,3,2,1
從第2項起,有些項大於它的前一項,有些項小於它的前一項的數列叫做擺動數列;
各項呈周期性變化的數列叫做周期數列(如三角函式);
各項相等的數列叫做常數列。如:2,2,2,2,2,2,2,2,2
通項公式:數列的第N項an與項的序數n之間的關係可以用一個公式表示,這個公式就叫做這個數列的通項公式。(註:通項公式不唯一)
遞推公式:如果數列{an}的第n項與它前一項或幾項的關係可以用一個式子來表示,那么這個公式叫做這個數列的遞推公式。
數列中數的總數為數列的項數。特別地,數列可以看成以正整數集N*(或它的有限子集{1,2,…,n})為定義域的函式an=f(n)。
如果可以用一個公式來表示,則它的通項公式是a(n)=f(n).
表示方法
如果數列{an}的第n項與序號n之間的關係可以用一個式子來表示,那么這個公式叫做這個數列的通項公式。如an=(-1)^(n+1)+1。
數列通項公式的特點:(1)有些數列的通項公式可以有不同形式,即不唯一。(2)有些數列沒有通項公式
如果數列{an}的第n項與它前一項或幾項的關係可以用一個式子來表示,那么這個公式叫做這個數列的遞推公式。如an=2a(n-1)+1(n>1)。
表示方法
如果數列{an}的第n項與序號n之間的關係可以用一個式子來表示,那么這個公式叫做這個數列的通項公式。如。數列通項公式的特點:(1)有些數列的通項公式可以有不同形式,即不唯一。(2)有些數列沒有通項公式
遞推公式。如=2+1(n>1)
數列遞推公式的特點:(1)有些數列的遞推公式可以有不同形式,即不唯一。(2)有些數列沒有遞推公式
有遞推公式不一定有通項公式
等差數列
定義一般地,如果一個數列從第2項起,每一項與它的前一項的差等於同一個常數,這個數列就叫做等差數列(arithmeticsequence),這個常數叫做等差數列的公差(commondifference),公差通常用字母d表示。
縮寫
等差數列可以縮寫為A.P.(ArithmeticProgression)。
等差中項
由三個數a,A,b組成的等差數列可以堪稱最簡單的等差數列。這時,A叫做a與b的等差中項(arithmeticmean)。
有關係:A=(a+b)/2
通項公式
an=a1+(n-1)d
an=Sn-S(n-1)(n≥2)
an=kn+b(k,b為常數)
前n項和
Sn=n(a1+an)/2=n*a1+n(n-1)d/2
Sn=(d/2)*n^2+(a1-d/2)n
性質
且任意兩項am,an的關係為:
an=am+(n-m)d
它可以看作等差數列廣義的通項公式。
從等差數列的定義、通項公式,前n項和公式還可推出:
a1+an=a2+an-1=a3+an-2=…=ak+an-k+1,k∈{1,2,…,n}
若m,n,p,q∈N*,且m+n=p+q,則有
am+an=ap+aq
S2n-1=(2n-1)an,S2n+1=(2n+1)an+1
Sk,S2k-Sk,S3k-S2k,…,Snk-S(n-1)k…成等差數列,等等。
和=(首項+末項)×項數÷2
項數=(末項-首項)÷公差+1
首項=2和÷項數-末項
末項=2和÷項數-首項
設a1,a2,a3為等差數列。則a2為等差中項,則2倍的a2等於a1+a3,即2a2=a1+a3。
套用
日常生活中,人們常常用到等差數列如:在給各種產品的尺寸劃分級別
時,當其中的最大尺寸與最小尺寸相差不大時,常按等差數列進行分級。
若為等差數列,且有an=m,am=n.則a(m+n)=0。
等比數列
定義一般地,如果一個數列從第2項起,每一項與它的前一項的比等於同一個常數,這個數列就叫做等比數列(geometricsequence)。這個常數叫做等比數列的公比(commonratio),公比通常用字母q表示。
縮寫
等比數列可以縮寫為G.P.(GeometricProgression)。
等比中項
如果在a與b中間插入一個數G,使a,G,b成等比數列,那么G叫做a與b的等比中項。
有關係:G^2=ab;G=±(ab)^(1/2)
註:兩個非零同號的實數的等比中項有兩個,它們互為相反數,所以G^2=ab是a,G,b三數成等比數列的必要不充分條件。
通項公式
an=a1q^(n-1)
an=Sn-S(n-1)(n≥2)
前n項和
當q≠1時,等比數列的前n項和的公式為
Sn=a1(1-q^n)/(1-q)=(a1-an*q)/(1-q)(q≠1)
當q=1時,等比數列的前n項和的公式為
Sn=na1
性質
任意兩項am,an的關係為an=am·q^(n-m)
(3)從等比數列的定義、通項公式、前n項和公式可以推出:a1·an=a2·an-1=a3·an-2=…=ak·an-k+1,k∈{1,2,…,n}
(4)等比中項:aq·ap=ar^2,ar則為ap,aq等比中項。
記πn=a1·a2…an,則有π2n-1=(an)2n-1,π2n+1=(an+1)2n+1
另外,一個各項均為正數的等比數列各項取同底數數後構成一個等差數列;反之,以任一個正數C為底,用一個等差數列的各項做指數構造冪Can,則是等比數列。在這個意義下,我們說:一個正項等比數列與等差數列是“同構”的。
性質:
①若m、n、p、q∈N*,且m+n=p+q,則am·an=ap·aq;
②在等比數列中,依次每k項之和仍成等比數列.
“G是a、b的等比中項”“G^2=ab(G≠0)”.
(5)等比數列前n項之和Sn=A1(1-q^n)/(1-q)
在等比數列中,首項A1與公比q都不為零.
注意:上述公式中A^n表示A的n次方。
套用
等比數列在生活中也是常常運用的。
如:銀行有一種支付利息的方式---複利。
即把前一期的利息和本金價在一起算作本金,
再計算下一期的利息,也就是人們通常說的利滾利。
按照複利計算本利和的公式:本利和=本金*(1+利率)^存期
如果一個數列從第2項起,每一項與它的前一項的比等於同一個常數,這個數列就叫做等比數列。這個常數叫做等比數列的公比,公比通常用字母q表示(q≠0)。
(1)等比數列的通項公式是:An=A1*q^(n-1)
若通項公式變形為an=a1/q*q^n(n∈N*),當q>0時,則可把an看作自變數n的函式,點(n,an)是曲線y=a1/q*q^x上的一群孤立的點。
(2)求和公式:Sn=nA1(q=1)
Sn=A1(1-q^n)/(1-q)
=(a1-a1q^n)/(1-q)
=a1/(1-q)-a1/(1-q)*q^n(即A-Aq^n)
(前提:q不等於1)
任意兩項am,an的關係為an=am·q^(n-m)
(3)從等比數列的定義、通項公式、前n項和公式可以推出:a1·an=a2·an-1=a3·an-2=…=ak·an-k+1,k∈{1,2,…,n}
(4)等比中項:aq·ap=ar^2,ar則為ap,aq等比中項。
記πn=a1·a2…an,則有π2n-1=(an)2n-1,π2n+1=(an+1)2n+1
另外,一個各項均為正數的等比數列各項取同底數後構成一個等差數列;反之,以任一個正數C為底,用一個等差數列的各項做指數構造冪Can,則是等比數列。在這個意義下,我們說:一個正項等比數列與等差數列是“同構”的。
等和數列
定義“等和數列”:在一個數列中,如果每一項與它的後一項的和都為同一個常數,那么這個數列叫做等和數列,這個常數叫做該數列的公和。
對一個數列,如果其任意的連續k(k≥2)項的和都相等,我們就把此數列叫做等和數列
性質
必定是循環數列
練習
1、下面一列整數中(每個字母或括弧都代表一個整數),任意相臨的3個整數的和都是20,則x+y+z=?x,2,(),(),(),4,(),y,(),(),z
2、(2004年湖南省理科實驗班聯合招生考試數學卷第2試第三題)圓周上放著120個正數(不一定是整數),今知其中任何相連的35個數的和都是200.證明:這些數中的每一個數都不超過30.(旁註:題目中“相連”即“相臨”之意)答案:第1題: x=14,y=2,z=2, 故: x+y+z=18; 第2題: (120,35)=5,使5個數為一組,每7組的和是200,那么每組有200/7<30所以每一個數都不超過30。列的通項求法
一般有
解題方法
an=Sn-Sn-1(n≥2)累和法(an-an-1=...an-1-an-2=...a2-a1=...將以上各項相加可得an)。
逐商全乘法(對於後一項與前一項商中含有未知數的數列)。
化歸法(將數列變形,使原數列的倒數或與某同一常數的和成等差或等比數列)。
特別數列
在等差數列中,總有SnS2n-SnS3n-S2n2(S2n-Sn)=(S3n-S2n)+Sn
即三者是等差數列,同樣在等比數列中。三者成等比數列
不動點法(常用於分式的通項遞推關係)
不動點法求數列通項
對於某些特定形式的數列遞推式可用不動點法來求
冪次數列表:
12345678910
22481632641282585121024
3392781243729
4416642561024
5525125625
66362161296
特殊數列的通項的寫法
1,2,3,4,5,6,7,8.......---------an=n1,1/2,1/3,1/4,1/5,1/6,1/7,1/8......-------an=1/n
2,4,6,8,10,12,14.......-------an=2n
1,3,5,7,9,11,13,15.....-------an=2n-1
-1,1,-1,1,-1,1,-1,1......--------an=(-1)^n
1,-1,1,-1,1,-1,1,-1,1......--------an=(-1)^(n+1)
1,0,1,0,1,0,1,01,0,1,0,1....------an=[(-1)^(n+1)+1]/2
1,0,-1,0,1,0,-1,0,1,0,-1,0......-------an=cos(n-1)π/2=sinnπ/2
9,99,999,9999,99999,.........------an=(10^n)-1
1,11,111,1111,11111.......--------an=[(10^n)-1]/9
衍生n,nn,nnn,nnnn,nnnnn......---------an=[(10^n)-1]*n/9,n為1-9的整數
1,4,9,16,25,36,49,.......------an=n^2
1,2,4,8,16,32......--------an=2^(n-1)
數列前N項和公式的求法
(一)1.等差數列:通項公式an=a1+(n-1)d首項a1,公差d,an第n項數
ak=ak+(n-k)dak為第k項數
若a,A,b構成等差數列則A=(a+b)/2
2.等差數列前n項和:
設等差數列的前n項和為Sn
即Sn=a1+a2+...+an;
那么Sn=na1+n(n-1)d/2
=dn^2(即n的2次方)/2+(a1-d/2)n
還有以下的求和方法:1,不完全歸納法2累加法3倒序相加法
(二)1.等比數列:
通項公式an=a1*q^(n-1)(即q的n-1次方)a1為首項,an為第n項
an=a1*q^(n-1),am=a1*q^(m-1)
則an/am=q^(n-m)
(1)an=am*q^(n-m)
(2)a,G,b若構成等比中項,則G^2=ab(a,b,G不等於0)
(3)若m+n=p+q則am×an=ap×aq
2.等比數列前n項和
設a1,a2,a3...an構成等比數列
前n項和Sn=a1+a2+a3...an
Sn=a1+a1*q+a1*q^2+....a1*q^(n-2)+a1*q^(n-1)(這個公式雖然是最基本公式,但一部分題目中求前n項和是很難用下面那個公式推導的,這時可能要直接從基本公式推導過去,所以希望這個公式也要理解)
Sn=a1(1-q^n)/(1-q)=(a1-an*q)/(1-q);
注:q不等於1;
Sn=na1注:q=1
求和一般有以下5個方法:1,完全歸納法(即數學歸納法)2累乘法3錯位相減法4倒序求和法5裂項相消法
著名的數列
等差數列典型例題:1/(1x(1+1))+1/(2x(2+1))+1/(3x(3+1))+1/(4x(4+1))+1/(5x(5+1))...............1/(n(n+1))求Sn
解析:
Sn=(1-1/2)+(1/2-1/3)+(1/3-1/4)+(1/4-1/5).............[1/n-1/(n+1)]
=1-1/(n+1)
大衍數列 0、2、4、8、12、18、24、32、40、50------
通項式:
an=(n×n-1)÷2(n為奇數)
an=n×n÷2(n為偶數)
前n項和公式:
Sn=(n-1)(n+1)(2n+3)÷12(n為奇數)
Sn=n(n+2)(2n-1)÷12(n為偶數)
大衍數列來源於《乾坤譜》,用於生原理。
斐波那契數列1、1、2、3、5、8、13、21、……
遞推公式為:F(1)=1,F(2)=1,F(n)=F(n-1)+F(n-2)
通項式
F(n)=(1/√5)*{[(1+√5)/2]^n-[(1-√5)/2]^n}
這樣一個完全是自然數的數列,通項公式居然是用無理數來表達的。
還可以發現Sn-2+Sn-1=Sn
定理口訣
等差等比兩數列,通項公式N項和。兩個有限求極限,四則運算順序換。數列問題多變幻,方程化歸整體算。數列求和比較難,錯位相消巧轉換,
取長補短高斯法,裂項求和公式算。歸納思想非常好,編個程式好思考:
一算二看三聯想,猜測證明不可少。還有數學歸納法,證明步驟程式化:
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |