定理套用
餘弦定理是解三角形中的一個重要定理,可套用於以下兩種需求:
當已知三角形的兩邊及其夾角,可由余弦定理得出已知角的對邊。
當已知三角形的三邊,可以由余弦定理得到三角形的三個內角。
求邊
餘弦定理公式可變換為以下形式:
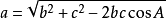 餘弦定理
餘弦定理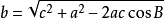 餘弦定理
餘弦定理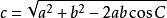 餘弦定理
餘弦定理因此,如果知道了三角形的兩邊及其夾角,可由余弦定理得出已知角的對邊。
三角函式
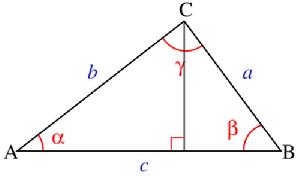 餘弦定理
餘弦定理如上圖所示,△ABC,在c上做高,將c邊寫:
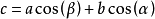 餘弦定理
餘弦定理將等式同乘以c得到:
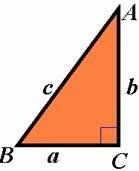 餘弦定理
餘弦定理運用同樣的方式可以得到:
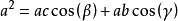 餘弦定理
餘弦定理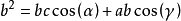 餘弦定理
餘弦定理將兩式相加:
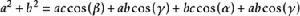 餘弦定理
餘弦定理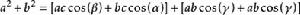 餘弦定理
餘弦定理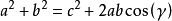 餘弦定理
餘弦定理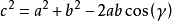 餘弦定理
餘弦定理向量
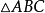 餘弦定理
餘弦定理中,
,
,
:
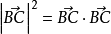 餘弦定理
餘弦定理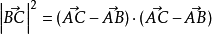 餘弦定理
餘弦定理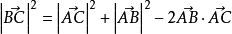 餘弦定理
餘弦定理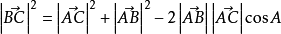 餘弦定理
餘弦定理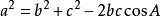 餘弦定理
餘弦定理求角
餘弦定理公式可變換為以下形式:
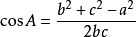 餘弦定理
餘弦定理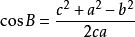 餘弦定理
餘弦定理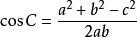 餘弦定理
餘弦定理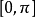 餘弦定理
餘弦定理因為餘弦函式在
上的單調性,可以得到:
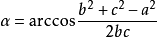 餘弦定理
餘弦定理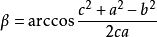 餘弦定理
餘弦定理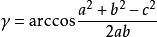 餘弦定理
餘弦定理因此,如果已知三角形的三條邊,可以由余弦定理得到三角形的三個內角。
歷史
餘弦定理的歷史可追溯至西元三世紀前歐幾里得的幾何原本,在書中將三角形分為鈍角和銳角來解釋,這同時對應現代數學中餘弦值的正負。
作用
(1)已知三角形的三條邊長,可求出三個內角
(2)已知三角形的兩邊及夾角,可求出第三邊。
(3)已知三角形兩邊及其一邊對角,可求其它的角和第三條邊。(見解三角形公式,推導過程略。)
判定定理一(兩根判別法):
若記m(c1,c2)為c的兩值為正根的個數,c1為c的表達式中根號前取加號的值,c2為c的表達式中根號前取
減號的值
①若m(c1,c2)=2,則有兩解
②若m(c1,c2)=1,則有一解
③若m(c1,c2)=0,則有零解(即無解)。
注意:若c1等於c2且c1或c2大於0,此種情況算到第二種情況,即一解。
判定定理二(角邊判別法):
一當a>bsinA時
①當b>a且cosA>0(即A為銳角)時,則有兩解
②當b>a且cosA<=0(即A為直角或鈍角)時,則有零解(即無解)
③當b=a且cosA>0(即A為銳角)時,則有一解
④當b=a且cosA<=0(即A為直角或鈍角)時,則有零解(即無解)
⑤當b
二當a=bsinA時
①當cosA>0(即A為銳角)時,則有一解
②當cosA<=0(即A為直角或鈍角)時,則有零解(即無解)
三當a
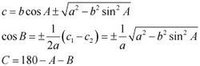 解三角形公式
解三角形公式解三角形公式
例如:已知△ABC的三邊之比為5:4:3,求最大的內角。
解 設三角形的三邊為a,b,c且a:b:c=5:4:3.
由三角形中大邊對大角可知:∠A為最大的角。由余弦定理
cos A=0
所以∠A=90°.
再如△ABC中,AB=2,AC=3,∠A=60度,求BC之長。
解 由余弦定理可知
BC2=AB2+AC2-2AB×AC·cos A
=4+9-2×2×3×cos60
=13-12x0.5
=13-6
=7
所以BC=√7. (注:cos60=0.5,可以用計算器算)
以上兩個小例子簡單說明了餘弦定理的作用。
平面幾何證法
在任意△ABC中 做AD⊥BC. ∠C所對的邊為c,∠B所對的邊為b,∠A所對的邊為a
則有BD=cosB*c,AD=sinB*c,DC=BC-BD=a-cosB*c
根據勾股定理可得:
AC^2=AD^2+DC^2
b^2=(sinB*c)^2+(a-cosB*c)^2
b^2=sin^2B*c^2+a^2+cos^2B*c^2-2ac*cosB
b^2=(sin^2B+cos^2B)*c^2-2ac*cosB+a^2
b^2=c^2+a^2-2ac*cosB
cosB=(c^2+a^2-b^2)/2ac
其他
從餘弦定理和餘弦函式的性質可以看出,如果一個三角形兩邊的平方和等於第三邊的平方,那么第三邊所對的角一定是直角,如果小於第三邊的平方,那么第三邊所對的角是鈍角,如果大於第三邊的平方,那么第三邊所對的角是銳角。即,利用餘弦定理,可以判斷三角形形狀。同時,還可以用餘弦定理求三角形邊長取值範圍。
解三角形時,除了用到餘弦定理外還常用正弦定理。
| | 30° | 45° | 60° | 75° |
| Sin | 1/2 | √2/2 | √3/2 | (√6+√2)/4 |
| Cos | √3/2 | √2/2 | 1/2 | (√6-√2)/4 |
| Tan | √3/3 | 1 | √3 | 2+√3 |
先考慮怎樣計算三角形第三邊的長
餘弦定理的實際套用
在實際生活中,餘弦定理是在計算機應有技術中的智慧型推薦系統,新聞分類中的基本算法之一。從吳軍的《數學之美》那本書上知道餘弦公式是可以對新聞進行分類的,當然就可以用來對用戶進行分類了。引用《數學之美》文章中的話:"向量實際上是多維空間中有方向的線段。如果兩個向量的方向一致,即夾角接近零,那么這兩個向量就相近。而要確定兩個向量方向是否一致,這就要用到餘弦定理計算向量的夾角了。" "當兩條新聞向量夾角的餘弦等於一時,這兩條新聞完全重複(用這個辦法可以刪除重複的網頁);當夾角的餘弦接近於一時,兩條新聞相似,從而可以歸成一類;夾角的餘弦越小,兩條新聞越不相關。 "同理,可以在推薦系統中用來計算用戶或者商品的相似性。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |
