概述
 算法
算法歷史發展
中國古代的籌算口決與珠算口決及其執行規則就是算法的雛形,這裡,所解決的問題類是算術運算。古希臘數學家歐幾里得在公元前3世紀就提出了一個算法,來尋求兩個正整數的最大公約數,這就是有名的歐幾里得算法,亦稱輾轉相除法。中國早已有“算術“、“算法”等辭彙,但是它們的含義是指當時的全部數學知識和計算技能,與現代算法的含義不盡相同。英文algorithm(算法)一詞也經歷了一個演變過程,最初的拼法為algorism或algoritmi,原意為用阿拉伯數字進行計算的過程。這個詞源於公元 9世紀波斯數字家阿爾·花拉子米的名字的最後一部分。
在古代,計算通常是指數值計算。現代計算已經遠遠地突破了數值計算的範圍,包括大量的非數值計算,例如檢索、表格處理、判斷、決策、形式邏輯演繹等。
在20世紀以前,人們普遍地認為,所有的問題類都是有算法的。20世紀初,數字家們發現有的問題類是不存在算法的,遂開始進行能行性研究。在這一研究中,現代算法的概念逐步明確起來。30年代,數字家們提出了遞歸函式、圖靈機等計算模型,並提出了丘奇-圖靈論題(見可計算性理論),這才有可能把算法概念形式化。按照丘奇-圖靈論題,任意一個算法都可以用一個圖靈機來實現,反之,任意一個圖靈機都表示一個算法。
按照上述理解,算法是由有限多個步驟組成的,它有下述兩個基本特徵:每個步驟都明確地規定要執行何種操作;每個步驟都可以被人或機器在有限的時間內完成。人們對於算法還有另一種不同的理解,它要求算法除了上述兩個基本特徵外,還要具有第三個基本特徵:雖然有些步驟可能被反覆執行多次,但是在執行有限多次之後,就一定能夠得到問題的解答。也就是說,一個處處停機(即對任意輸入都停機)的圖靈機才表示一個算法,而每個算法都可以被一個處處停機的圖靈機來實現
算法分類
 算法
算法算法可以宏泛的分為三類:
有限的,確定性算法 這類算法在有限的一段時間內終止。他們可能要花很長時間來執行指定的任務,但仍將在一定的時間內終止。這類算法得出的結果常取決於輸入值。
有限的,非確定算法 這類算法在有限的時間內終止。然而,對於一個(或一些)給定的數值,算法的結果並不是唯一的或確定的。
無限的算法 是那些由於沒有定義終止定義條件,或定義的條件無法由輸入的數據滿足而不終止運行的算法。通常,無限算法的產生是由於未能確定的定義終止條件。
算法特徵
1、輸入項:一個算法有零個或多個輸入,以刻畫運算對象的初始情況。例如,在歐幾里得算法中,有兩個輸入,即m和n。
2、確定性:算法的每一個步驟必須要確切地定義。即算法中所有有待執行的動作必須嚴格而不含混地進行規定,不能有歧義性。例如,歐幾里得算法中,步驟1中明確規定“以m除以n,而不能有類似以m除n以或n除以m這類有兩種可能做法的規定。
3、有窮性:一個算法在執行有窮步滯後必須結束。也就是說,一個算法,它所包含的計算步驟是有限的。例如,在歐幾里得算法中,m和n均為正整數,在步驟1之後,r必小於n,若r不等於0,下一次進行步驟1時,n的值已經減小,而正整數的遞降序列最後必然要終止。因此,無論給定m和n的原始值有多大,步驟1的執行都是有窮次。
4、輸出:算法有一個或多個的輸出,即與輸入有某個特定關係的量,簡單地說就是算法的最終結果。例如,在歐幾里得算法中只有一個輸出,即步驟2中的n。
5、能行性:算法中有待執行的運算和操作必須是相當基本的,換言之,他們都是能夠精確地進行的,算法執行者甚至不需要掌握算法的含義即可根據該算法的每一步驟要求進行操作,並最終得出正確的結果。
算法要素
數據的運算和操作
 算法
算法1.算術運算:加減乘除等運算
2.邏輯運算:或、且、非等運算
3.關係運算:大於、小於、等於、不等於等運算
4.數據傳輸:輸入、輸出、賦值等運算
算法的控制結構
一個算法的功能結構不僅取決於所選用的操作,而且還與各操作之間的執行順序有關。
算法評定
算法的複雜度1.時間複雜度:算法的時間複雜度是指算法需要消耗的時間資源。
2.空間複雜度:算法的空間複雜度是指算法需要消耗的空間資源。其計算和表示方法與時間複雜度類似,一般都用複雜度的漸近性來表示。
3.正確性:算法的正確性是評價一個算法優劣的最重要的標準。
4.可讀性:算法的可讀性是指一個算法可供人們閱讀的容易程度。
5.健壯性:是指一個算法對不合理數據輸入的反應能力和處理能力,也稱為容錯性。
描述方式
1、用自然語言描述算法
前面關於歐幾里的算法以及算法實例的描述,使用的都是自然語言。自然語言是人們日常所用的語言,如漢語、英語、德語等。使用這些語言不用專門訓練,所描述的算法也通俗易懂。
2、用流程圖描述算法
在數學課程里,我們學習了用程式框圖來描述算法。在程式框圖中流程圖是描述算法的常用工具由一些圖形符號來表示算法。
3、用偽代碼描述算法
偽代碼是用介於自然語言和計算機語言之間的文字和符號來描述算法的工具。它不用圖形符號,因此,書寫方便、格式緊湊,易於理解,便於向電腦程式設計語言過度。
史料記載
 算法
算法自唐代以來,歷代更有許多專門論述“算法”的專著:
唐代:《一位算法》一卷,《算法》一卷;
宋代:《算法緒論》一卷、《算法秘訣》一卷;最著名的是楊輝的《楊輝算法》;
元代:《丁巨算法》;
明代:程大位《算法統宗》
清代:《開平算法》、《算法一得》、《算法全書》。
而英文名稱Algorithm來自於9世紀波斯數學家al-Khwarizmi,因為al-Khwarizmi在數學上提出了算法這個概念。“算法”原為"algorism,意思是阿拉伯數字的運算法則,在18世紀演變為"algorithm"。歐幾里得算法被人們認為是史上第一個算法。第一次編寫程式是AdaByron於1842年為巴貝奇分析機編寫求解解伯努利方程的程式,因此AdaByron被大多數人認為是世界上第一位程式員。因為查爾斯·巴貝奇(CharlesBabbage)未能完成他的巴貝奇分析機,這個算法未能在巴貝奇分析機上執行。因為"well-definedprocedure"缺少數學上精確的定義,19世紀和20世紀早期的數學家、邏輯學家在定義算法上出現了困難。20世紀的英國數學家圖靈提出了著名的圖靈論題,並提出一種假想的計算機的抽象模型,這個模型被稱為圖靈機。圖靈機的出現解決了算法定義的難題,圖靈的思想對算法的發展起到了重要作用的。求素數的埃拉托塞尼篩法和求方根的開方的方法公式(算法不等於公式,公式卻是提供一種算法)
基本方法
1.遞推法
 算法
算法2.遞歸法
遞歸指的是一個過程:函式不斷引用自身,直到引用的對象已知
3.窮舉搜尋法
窮舉搜尋法是對可能是解的眾多候選解按某種順序進行逐一枚舉和檢驗,並從眾找出那些符合要求的候選解作為問題的解。
4.貪婪法
貪婪法是一種不追求最優解,只希望得到較為滿意解的方法。貪婪法一般可以快速得到滿意的解,因為它省去了為找最優解要窮盡所有可能而必須耗費的大量時間。貪婪法常以當前情況為基礎作最優選擇,而不考慮各種可能的整體情況,所以貪婪法不要回溯。
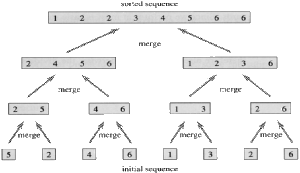
5.分治法
分治法是把一個複雜的問題分成兩個或更多的相同或相似的子問題,再把子問題分成更小的子問題……直到最後子問題可以簡單的直接求解,原問題的解即子問題的解的合併。
6.動態規劃法
動態規劃是一種在數學和計算機科學中使用的,用於求解包含重疊子問題的最最佳化問題的方法。其基本思想是,將原問題分解為相似的子問題,在求解的過程中通過子問題的解求出原問題的解。動態規劃的思想是多種算法的基礎,被廣泛套用於計算機科學和工程領域。
7.疊代法
疊代法是數值分析中通過從一個初始估計出發尋找一系列近似解來解決問題(一般是解方程或者方程組)的過程,為實現這一過程所使用的方法統稱為疊代法。
8.分支界限法
與貪婪算法一樣,這種方法也是用來為組合最佳化問題設計求解算法的,所不同的是它在問題的整個可能解空間搜尋,所設計出來的算法雖其時間複雜度比貪婪算法高,但它的優點是與窮舉法類似,都能保證求出問題的最佳解,而且這種方法不是盲目的窮舉搜尋,而是在搜尋過程中通過限界,可以中途停止對某些不可能得到最優解的子空間進一步搜尋(類似於人工智慧中的剪枝),故它比窮舉法效率更高。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |