等比數列
一般地，如果一個數列的首項不為0，且從第二項起，每一項與它的前一項的比等於同一個常數，那么這個數列就叫做 等比數列，這個常數叫做等比數列的 公比，公比通常用字母q表示( q不等於0）。如數列2，4，8，16就為等比數列。
等比數列在生活中也是常常運用的。如：銀行有一種支付利息的方式——複利。即把前一期的利息和本金加在一起算作本金，在計算下一期的利息，也就是人們通常說的“利滾利”。
等比中項簡介
在等比數列a項和b項中，插入一個數G使a、G、b成等比數列，那么G叫做a、b的等比中項 。
若a和b的等比中項為c，則c的平方等於a和b的乘積。
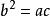等比中項若a，b，c成等比數列，則有
相關結論
等比中項
等比中項由，可知成立。
等比中項 等比中項還可由，得。
此結論說明，在等比數列中，從第二項起，每一項（有限數列末項除外）都是它前後兩項的等比中項。
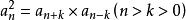等比中項同樣可證得成立。
此結論說明，在等比數列中，任取數列中的某項都是與它前後等距離的兩項的等比中項（保證前後兩項都存在）。
性質
等比中項同號的兩個數才有等比中項；等比中項有兩個，且互為相反數。
在等比數列中，若2m=p+k,m與p,k∈N*，則，
舉例
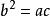等比中項在解決一些數學問題時，如果發現其中存在特徵，我們不妨聯想到等比中項的知識，巧設公比，利用q的橋樑作用解題，不僅思路新穎而且過程簡捷，從而為問題的解決提供了一種新的方法。
（1）等比數列4，9求該數列等比中項
解：設給數列等比數列為C 則
C/4=9/C
C=36
C=±6
（2）在三角函式的套用：
等比中項
等比中項已知，且a為第三象限角，求。
等比中項
等比中項因為，所以。
等比中項
等比中項設，。
等比中項所以，
等比中項
等比中項又位於第三象限，所以，。
（3）在解方程的套用
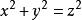等比中項
等比中項已知x，y，z屬於正實數集，且，
等比中項求證：
等比中項
等比中項
等比中項由知，，所以等比數列。
等比中項
等比中項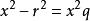設，
等比中項得
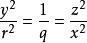等比中項所以。
