理論發展
匈牙利著名數學家P·羅莎在她的名著《無窮的玩藝》一書中曾對“化歸法”作過生動的比擬.她寫道:“假設在你面前有煤氣灶、水龍頭、水壺和火柴,現在的任務是要燒水,你應當怎樣去做?”.正確的回答是:“在水壺中放上水,點燃煤氣,再把水壺放到煤氣灶上.”接著羅莎又提出第二個問題:“假設所有的條件都不變,只是水壺中已有了足夠的水,這時你應該怎樣去做?”.對此,人們往往回答說:“點燃煤氣,再把壺放到煤氣灶上.”但羅莎認為這並不是最好的回答,因為“只有物理學家才這樣做,而數學家則會倒去壺中的水,並且聲稱我已經把後一問題化歸成先前的問題了.”
 化歸法
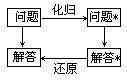
化歸法羅莎的比喻固然有點誇張,但卻道出了化歸的根本特徵:在解決一個問題時人們的眼光並不落在問題的結論上,而是去尋覓、追溯一些熟知的結果,儘管向前走兩步,也許能達到目的,但我們也情願退一步回到原來的問題上去.利用化歸法解決問題的過程可以簡單地用以下框圖表示:(右圖)
套用實例
化歸法是一種分析問題解決問題的基本思想方法.在數學中通常的作法是:將一個非基本的問題通過分解、變形、代換…,或平移、鏇轉、伸縮…等多種方式,將它化歸為一個熟悉的基本的問題,從而求出解答.如學完一元一次方程、因式分解等知識後,學習一元二次方程我們就是通過因式分解等方法,將它化歸為一元一次方程來解的.後來我們學到特殊的一元高次方程時,又是化歸為一元一次和一元二次方程來解的.對一元不等式也有類似的作法.又如在平面幾何中我們在學習了三角形的內角和、面積計算等有關定理後,對n邊形的內角和、面積的計算,也是通過分解、拼合為若干個三角形來加以解決的.再如在解析幾何中,當我們學完了最基本、最簡單的圓錐曲線知識以後,對一般圓錐曲線的研究,我們也是通過坐標軸平移或鏇轉,化歸為基本的圓錐曲線(在新坐標系中)來實現的.其它如幾何問題化歸為代數問題,立體幾何問題化歸為平面幾何問題,任意角的三角函式問題化歸為銳角三角函式問題來表示的例子就更多了.所以,掌握化歸的思想方法對於數學學習有著重要的意義.總之,化歸的原則是以已知的、簡單的、具體的、特殊的、基本的知識為基礎,將未知的化為已知的,複雜的化為簡單的,抽象的化為具體的,一般的化為特殊的,非基本的化為基本的,從而得出正確的解答.