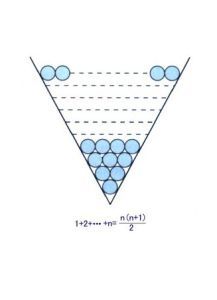
公式
通項公式
如果一個等差數列的首項為a1,公差為d,那么該等差數列第n項的表達式為:
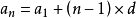 等差數列
等差數列即
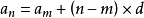 等差數列
等差數列補充:
求和公式
若一個等差數列的首項為a1,末項為an那么該等差數列和表達式為:
S=(a1+an)n÷2
即(首項+末項)×項數÷2
前n項和公式
注意:n是正整數(相當於n個等差中項之和)
等差數列前N項求和,實際就是梯形公式的妙用:
上底為:a1首項,下底為a1+(n-1)d,高為n。
即[a1+a1+(n-1)d]* n/2=a1 n+ n (n-1)d /2.
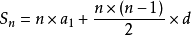 等差數列
等差數列推論
一.從通項公式可以看出,a(n)是n的一次函式(d≠0)或常數函式(d=0),(n,an)排在一條直線上,由前n項和公式知,S(n)是n的二次函式(d≠0)或一次函式(d=0,a1≠0),且常數項為0。
二. 從等差數列的定義、通項公式,前n項和公式還可推出:a(1)+a(n)=a(2)+a(n-1)=a(3)+a(n-2)=…
=a(k)+a(n-k+1),(類似:p(1)+p(n)=p(2)+p(n-1)=p(3)+p(n-2)=...=p(k)+p(n-k+1)),k∈{1,2,…,n}
三.若m,n,p,q∈N*,且m+n=p+q,則有a(m)+a(n)=a(p)+a(q),S(2n-1)=(2n-1)*a(n),S(2n+1)=
(2n+1)*a(n+1),S(k),S(2k)-S(k),S(3k)-S(2k),…,S(n)*k-S(n-1)*k…成等差數列,等等。
若m+n=2p,則a(m)+a(n)=2*a(p)
(對3的證明:p(m)+p(n)=b(0)+b(1)*m+b(0)+b(1)*n=2*b(0)+b(1)*(m+n)
p(p)+p(q)=b(0)+b(1)*p+b(0)+b(1)*q=2*b(0)+b(1)*(p+q);因為m+n=p+q,所以p(m)+p(n)=p(p)+p
(q))
四.其他推論
① 和=(首項+末項)×項數÷2
(證明:s(n)=[n,n^2]*[1,1/2;0,1/2]*[b(0);b(1)]=n*b0+1/2*b1*n+1/2*b1*n^2
(p(1)+p(n))*n/2=(b(0)+b(1)+b(0)+b(1)*n)*n/2=n*b0+1/2*b1*n+1/2*b1*n^2=s(n))
證明原理見高斯算法
項數=(末項-首項)÷公差+1
(證明:(p(n)-p(1))/b(1)+1=(b(0)+b(1)*n-(b(0)+b(1)))/b(1)+1=(b(1)*(n-1))/b(1)+1=n-1+1=n)
② 首項=2x和÷項數-末項或末項-公差×(項數-1)
③ 末項=2x和÷項數-首項
(以上2項為第一個推論的轉換)
④ 末項=首項+(項數-1)×公差
(上一項為第二個推論的轉換)
推論3證明
若m,n,p,q∈N*,且m+n=p+q,則有a(m)+a(n)=a(p)
+a(q)
如a(m)+a(n)=a(1)+(m-1)*d+a(1)+(n-1)*d
=2*a(1)+(m+n-2)*d
同理得,
a(p)+a(q)=2*a(1)+(p+q-2)*d
又因為
m+n=p+q ;
a(1),d均為常數
所以
若m,n,p,q∈N*,且m+n=p+q,則有a(m)+a(n)=a(p)+a(q)
若m,n,p∈N*,且m+n=2p,則有a(m)+a(n)=2a(p)
註:1.常數列不一定成立
2.m,p,q,n屬於自然數
⑤2(前2n項和-前n項和)=前n項和+前3n項和-前2n項和
等差中項
等差中項即等差數列頭尾兩項的和的一半.但求等差中項不一定要知道頭尾兩項.
等差數列中,等差中項一般設為A(r).當A(m),A(r),A(n)成等差數列時。
A(m)+A(n)=2×A(r),所以A(r)為A(m),A(n)的等差中項,且
為數列的平均數。並且可以推知n+m=2×r。
且任意兩項a(m),a(n)的關係為:a(n)=a(m)+(n-m)*d,(類似p(n)=p(m)+(n-m)*b(1),相當容易證明
它可以看作等差數列廣義的通項公式。
等差數列的套用日常生活中,人們常常用到等差數列如:在給各種產品的尺寸劃分級別
時,當其中的最大尺寸與最小尺寸相差不大時,常按等差數列進行分級。
若為等差數列,且有a(n)=m,a(m)=n.則a(m+n)=0。
其實,中國古代南北朝的張丘建早已在《張丘建算經》提到等差數列了:
今有女子不善織布,逐日所織的布以同數遞減,初日織五尺,末一日織一尺,計織三十日,問共織幾何?
書中的解法是:並初、末日織布數,半之,余以乘織訖日數,即得。
這相當於給出了S(n)=(a(1)+a(n))/2*n的求和公式。
等差數列小故事
高斯是德國數學家、天文學家和物理學家,被譽為歷史上偉大的數學家之一,和阿基米德、牛頓並列,同享盛名。
 等差數列
等差數列高斯1777年4月30日生於不倫瑞克的一個工匠家庭,1855年2月23日卒于格丁根。幼時家境貧困,但聰敏異常,受一貴族資助才進學校受教育。1795~1798年在哥廷根大學學習1798年轉入黑爾姆施泰特大學,翌年因證明代數基本定理獲博士學位。從1807年起擔任哥廷根大學教授兼哥廷根天文台台長直至逝世。
高斯7歲那年,父親送他進了耶卡捷林寧國民國小,讀書不久,高斯在數學上就顯露出了常人難以比較的天賦,最能證明這一點的是高斯十歲那年,教師彪特耐爾布置了一道很繁雜的計算題,要求學生把1到 100的所有整數加起來,教師剛敘述完題目,高斯即刻把寫著答案的小石板交了上去。彪特耐爾起初並不在意這一舉動,心想這個小傢伙又在搗亂,但當他發現全班唯一正確的答案屬於高斯時,才大吃一驚。而更使人吃驚的是高斯的算法,他發現:第一個數加最後一個數是101,第二個數加倒數第二個數的和也是101,……共有50對這樣的數,用101乘以50得到5050。這種算法是教師未曾教過的計算等級數的方法,高斯的才華使彪特耐爾十分激動,下課後特地向校長匯報,並聲稱自己已經沒有什麼可教高斯的了。
基本性質
⑴數列為等差數列的重要條件是:數列的前n項和S 可以寫成S = an^2 + bn的形式(其中a、b為常數).
⑵在等差數列中,當項數為2n (n∈ N+)時,S偶-S奇 = nd,S奇÷S偶=an÷a(n+1);當項數為(2n-1)(n∈ N+)時,S奇—S偶=a(中),S奇-S偶=項數*a(中) ,S奇÷S偶 =n÷(n-1).
⑶若數列為等差數列,則Sn,S2n -Sn ,S3n -S2n,…仍然成等差數列,公差為k^2d .
(4)若數列{an}與{bn}均為等差數列,且前n項和分別是Sn和Tn,則am/bm=S2m-1/T2m-1.
⑸在等差數列中,S = a,S = b (n>m),則S = (a-b).
⑹等差數列中, 是n的一次函式,且點(n, )均在直線y = x + (a - )上.
⑺記等差數列的前n項和為S .①若a >0,公差d<0,則當a ≥0且an+1≤0時,S 最大;②若a <0 ,公差d>0,則當a ≤0且an+1≥0時,S 最小.
[8)若等差數列S(p)=q,S(q)=p,則S(p+q)=-(p+q)
r次等差數列
為什麼等差數列的學習中,對公差和首項特別的關注,因為公差和首項可以作為等差數列一切變化的切入點。當我們有更好的切入點後,我們可以毫不猶豫的拋棄公差和首項。
假設一個基En(x)=[1,x,x^2,...,x^k],轉換矩陣A為k+1階方陣,b=[b0,b1,b2,...,bk]。b同En的長度一樣(k+1)。b'表示b的轉置。當k=1時,我們可以稱為一次數列。k=r時,我們可以稱為r次數列。(x,k只能取自然數)
p(x)=En(x)*b'
s(x)=x*En(x)*A*b'
m+n=p+q(m、n、p、q∈N*)則am+an=ap+aq
一次數列的性質
1.p1(x),p2(x)均為一次數列,則p1(x)±p2(x)與c*p1(x)±p2(x)(c為非零常數)也是一次數列。p(x)是一次函式,(n,p(x))構成直線。
2.p(m)-p(n)=En(m)*b'-En(n)*b'=(En(m)-En(n))*b'=[0,m-n]*b'
3.m+n=p+q -> p(p)+p(q)=p(m)+p(n)
(證明:m+n=p+q -> En(m)+En(n)=En(p)+En(q)
p(m)+p(n)=En(m)*b'+En(n)*b'=(En(m)+En(n))*b'
p(p)+p(q)=(En(p)+En(q))*b'=(En(m)+En(n))*b'=p(m)+p(n)
4.從p(x)=En(x)*b'中取出等距離的項,構成一個新數列,此數列仍是一次數列,其一次項係數為k*b(1)( k為取出項數之差),常項係數未知。
5.在一次數列中,從第二項起,每一項(有窮數列末項除外)都是它前後兩項的平均數.
6.當一次項係數b(1)>0時,數列中的數隨項數的增大而增大;當b(1)<0時,數列中的數隨項數的減少而減小;b(1)=0時,數列中的數等於一個常數.
等差數列的判定
1、a(n+1)--a(n)=d (d為常數、n ∈N*)[或a(n)--a(n-1)=d,n ∈N*,n ≥2,d是常數]等價於{a(n)}成等差數列。
2、2a(n+1)=a(n)+a(n+2) [n∈N*] 等價於{a(n)}成等差數列。
3、a(n)=kn+b [k、b為常數,n∈N*] 等價於{a(n)}成等差數列。
4、S(n)=A(n)^2 +B(n) [A、B為常數,A不為0,n ∈N* ]等價於{a(n)}為等差數列。
一道例題
1.設p(x)為一次數列,s(7)=7,s(15)=75,t(x)=s(x)/x,求T(x),其中x為自然數
[s(7);s(15)]=[7*En(7);15*En(15)]*A*b'=[7;75] ->b'=A^-1*[7*En(7);15*En(15)]^-1*[7;75]t(x)=s(x)/x=x*En(x)*A*b'/x=En(x)*A*b' ->st(x)=x*En(x)*A^2*b'=x*En(x)*A^2*A^-1*[7*En(7);15*En(15)]^-1=x*En(x)*A*[7*En(7);15*En(15)]^-1*[7;75]=-9/4*x+1/4*x^2(注意:其中st(x)表示t(x)的和)
特殊性質
在有窮等差數列中,與首末兩項距離相等的兩項和相等。並且等於首末兩項之和;特別的,若項數為奇數,還等於中間項的2倍,
即,a(1)+a(n)=a(2)+a(n-1)=a(3)+a(n-2)=···=2*a中
例:
數列:1,3,5,7,9,11中
a(1)+a(6)=12 ; a(2)+a(5)=12 ; a(3)+a(4)=12 ; 即,在有窮等差數列中,與首末兩項距離相等的兩項和相等。並且等於首末兩項之和。
數列:1,3,5,7,9中
a(1)+a(5)=10 ; a(2)+a(4)=10 ; a(3)=5=[a(1)+a(5)]/2=[a(2)+a(4)]/2=10/2=5 ; 即,若項數為奇數,和等於中間項的2倍,另見,等差中項.
餘數
1、當合數是由單個素因子組成時,如由單個素因子3組成的合數9,27,81等,等差數列的公差能夠被該單個素因子整除時,該等差數列除以合數的餘數為:9/3=3個,27/3=9個,81/3=27個循環排列。具體餘數為該等差數列的首項/素因子的餘數+素因子*L所得。如首項/3餘1,其餘數為1+3L,例如等差數列1+30N數列除以合數9餘數按1,4,7進行循環;如首項/3餘0,其餘數為0+3L,例如等差數列3+30N數列除以合數9的餘數按3,6,0進行循環。
2、當公差能被合數整時,該等差數列除以合數的餘數,為等差數列的首項除以該合數的餘數。如等差數列3+30N的數除以合數15的餘數,都為首項的3/15的餘數3。
3、當等差數列的公差能夠被合數分解出現的部分素因子整除。
(1)單素因子:其餘數個數與不能整除的素因子的值相同,具體餘數為首項除以能整除的素因子的餘數+該素因子*L。如等差數列3+30N的數除以35,因首項的3/5餘3,有3+5L=3,8,13,18,23,28,33。具體餘數為3,33,28,23,18,13,8的循環排列。
(2)多素因子:其餘數個數與不能整除的素因子之積的值相同,具體餘數為首項除以能整除的素因子的共同餘數+素因子之積*L。如2137+2310N數列除以合數46410,公差2310為2*3*5*7*11,合數46410為2*3*5*7*13*17,共同的素因子為2,3,5,7,因首項2137/2餘1,2137/3餘1,2137/5餘2,2137/7餘2,滿足這些條件的數為37,37是它們的共同餘數。具體餘數為37+210L中的數,取13*17=221個餘數循環,具體餘數以2137,4447,6567,…, 46237,共221項為一個循環周期。
4、當等差數列的公差不能被合數分解出來的素因子整除時,其餘數個數為合數的值,如等差數列7+43N除以合數10,其餘數為10個:0,1,2,3,4,5,6,7,8,9,具體餘數為7,0,3,6,9,2,5,8,1,4的循環排列。
相鄰兩項之間的差為常數的一類數列或者任意相鄰兩項的差相等的數列。
等差數列的遞推公式an=a(n-1)+d d為公差 an為第n項 a(n-1)為第n-1項
通項公式an=a1+(n-1)d
前n項和S(n)=n*a(1)+n*(n-1)*d/2或S(n)=n*(a(1)+a(n))/2
等差數列前n項和公式S 的基本性質
⑴數列為等差數列的重要條件是:數列的前n項和S 可以寫成S = an^2 + bn的形式(其中a、b為常數).
⑵在等差數列中,當項數為2n (n∈ N+)時,S偶-S奇 = nd, S奇÷S偶=an÷a(n+1) ;當項數為(2n-1)(n∈ N+)時,S奇—S偶=a中 ,S奇÷S偶 =n÷(n-1) .
⑶若數列為等差數列,則S n,S2n -Sn ,S3n -S 2n,…仍然成等差數列,公差為k^2d .
⑷若兩個等差數列的前n項和分別是S 、T (n為奇數),則 = .
⑸在等差數列中,S = a,S = b (n>m),則S = (a-b).
⑹等差數列中, 是n的一次函式,且點(n, )均在直線y = x + (a - )上.
(7)記等差數列{an}的前n項和為Sn:①若a1>0,公差d<0,則當an≥0且an+1≤0時,S最大;②若a1<0,公差d>0,則當an≤0且an+1≥0時,S最小。
(8)若等差數列S(p)=q,S(q)=p,則S(p+q)=-(p+q)
等差數列在高中數學人教版必修5
經典試題
高一數學經典試題:兩數列{an}{bn}滿足bn=(a1+2a2+3a3+...nan)/(1+2+3+..+n)若{bn}是等差數列,求證{an}也是等差數列。
高一數學經典試題解析:bn=(a1+2a2+3a3+...nan)/(1+2+3+..+n)
=(a1+2a2+3a3+....nan)/(n+n^2)/2
∴(n+n^2)bn=2(a1+2a2+3a3+....nan).......................1
∴[(n+1)+(n+1)^2]b(n+1)=2[a1+2a2+3a3+....(n+1)a(n+1)].............2
由1式-2式得:
(n+n^2)bn-(n^2+3n+2)b(n+1)=-2(n+1)an+1.............3
若{bn}是等差數列設其公差d
則bn=b(n+1)-d...............4
將4式代入3式得
an+1=(2bn+1+nd)/2=bn+1+nd/2.......5
又∵b(n+1)=b1+nd代入5式
得an+1=b1+nd+nd/2=b1+3n/2d
由bn=(a1+2a2+3a3+...nan)/(1+2+3+..+n)知當n=1時b1=a1
∴an+1=a1+3n/2d
∴an=a1+(n-1)*(2/3)d
∴{an}也是等差數列.公差為(2/3)d
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |