定義
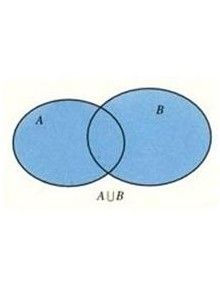
由所有屬於A或屬於B的元素所組成的集合，叫做A,B的並集。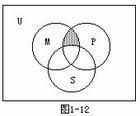
陰影表示並集表示
A∪B讀作：A並B性質：A∪A=A A∪Φ = ΦA∪B=B∪A
難點
弄清交集與並集的概念、符號之間的區別與聯繫；關鍵是要能達到會正確表示一些簡單集合的目標；並集講解
一般地，由所有屬於集合A或屬於集合B的元素所組成的集合，稱為集合A與B的並集（Union）記作：A∪B讀作：“A並B”
即：A∪B={x|x∈A，或x∈B}
說明：兩個集合求並集，結果還是一個集合，是由集合A與B的所有元素組成的集合（重複元素只看成一個元素）。
例題1求集合A與B的並集
①A={6，8，10，12}B={3，6，9，12}
②A={x|-1≤x≤2}B={x|0≤x≤3}
（過度）問題：在上圖中我們除了研究集合A與B的並集外，它們的公共部分（即問號部分）還應是我們所關心的，我們稱其為集合A與B的交集。
學習過程
1.由所有屬於集合A且屬於集合B的元素所組成的集合，叫做A、B的交集，記作A∩B。即A∩B=2.韋恩圖表示（分五種情況顯示）
說明：交集的意義：A∩B=，即A∩B是所有A、B中的元素組成的集合，因此，A∩B中的元素既有集合A的屬性，又有集合B的屬性。
3.由所有屬於集合A或屬於集合B的元素所組成的集合，叫做A、B的並集，記作A∪B。即A∪B=
4.韋恩圖表示（分五種情況顯示）
說明：並集的意義：A∪B=，即A∪B是所有A、B中的元素組成的集合，因此，A∪B中的元素至少具有集合A或集合B的屬性之一。
5.例題分析：例題1、2、3、4、5、6、7、8
在求交集時，應先識別集合的元素屬性及範圍，並化簡集合，對於數集可以藉助於數軸直觀，以形助數得出交集。
6.區分交集與並集的關鍵是“且”與“或”，在處理有關交集與並集的問題時，常常從這兩個字眼出發去揭示、挖掘題設條件，進而用集合語言表達。
7.課堂練習
（1）設A=、B=，則A∩Z=A，B∩Z=B，A∩B=
（2）設A=、B=，則A∪Z=Z，B∪Z=Z，A∪B=Z
8.關於交集有如下性質
A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A
9.關於並集有如下性質
AA∪B，BA∪B，A∪A=A，A∪=A,A∪B=B∪A
10.若A∩B=A，則AB，反之也成立
若A∪B=B，則AB，反之也成立
若x∈（A∩B），則x∈A且x∈B
若x∈（A∪B），則x∈A，或x∈B
11.注意AB，A∩B=A，A∪B=B這些關係的等價性。
數學名詞
A-F▪八邊形 ▪八面體 ▪百分比 ▪百分點
▪百分位數 ▪半徑 ▪半球 ▪半圓
▪被乘數 ▪被除數 ▪被加數 ▪被減數
▪比 ▪比例 ▪邊 ▪變數
▪標準差 ▪表面積 ▪並集 ▪補集
▪不等邊三角形 ▪不等式 ▪不定積分 ▪差
▪長 ▪常量 ▪乘 ▪乘方
▪乘數 ▪除 ▪除數 ▪垂心
▪次方 ▪次方根 ▪大於 ▪大於等於
▪代數 ▪單調性 ▪單項式 ▪導數
▪等邊三角形 ▪等式方程式 ▪等腰三角形 ▪等腰梯形
▪等於 ▪底 ▪底面 ▪點
▪定積分 ▪定理 ▪定義域 ▪對數
▪鈍角 ▪鈍角三角形 ▪多邊形 ▪多面體
▪二次方程 ▪多項式 ▪二次方根平方根 ▪二次方平方
▪二進制 ▪二十面體 ▪反餘割 ▪反餘切
▪反餘弦 ▪反正割 ▪反正切 ▪反正弦
▪方差 ▪非常態分配 ▪分布 ▪分母
▪分數 ▪分子 ▪負 ▪複數
以上名詞按中文名拼音首字母順序排列
G-L
M-R
S-Z
盤點高中數學名詞
| 高中是大學的過渡階段，學好高中數學，才能為學好大學數學打好基礎，那我們盤點下高中數學中有哪些名詞吧。 |
