數列
數列（sequence of number）是以正整數集（或它的有限子集）為定義域的函式，是一列有序的數。數列中的每一個數都叫做這個數列的項。排在第一位的數稱為這個數列的第1項（通常也叫做首項），排在第二位的數稱為這個數列的第2項，以此類推，排在第n位的數稱為這個數列的第n項，通常用an表示。
數列的一般形式簡記為{an}。
數列中的項必須是數，它可以是實數，也可以是複數。
用符號{an}表示數列，只不過是“借用”集合的符號，它們之間有本質上的區別：1.集合中的元素是互異的，而數列中的項可以是相同的。2.集合中的元素是無序的，而數列中的項必須按一定順序排列，也就是必須是有序的。
著名的數列有斐波那契數列，三角函式，卡特蘭數，楊輝三角等。
項數有限的數列為“有窮數列”（finite sequence）。
項數無限的數列為“無窮數列”（infinite sequence）。
介紹
數列中的項無窮多的數列叫做無窮數列。形如：1,2,3,4,5,6...就是一個無窮的等差數列。
特點
有省略號的，未知字母不加約束條件的，與實際無關，未說明有效數字位數的。
通項公式
在人教社高中數學新教材(試驗修訂本·必修)第一冊(上)《數列》一章的開頭，就提到如下無窮數列：
無窮數列的精確到1,0.1,0.01,0.001,…的不足近似值構成的數列：1,1.4,1.41,1.414,… .
實際上，像這樣的數列在中學數學教學中經常遇到，可以統一歸結為以下一類無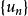窮數列：
無窮數列若α為無理數,將α依次精確到個位，十分位，百分位，千分位，…的不足(或過剩)近似值構成的數列。
其實，我們僅用大家熟知的函式{x}(表示實數x的小數部分)，就能十分方便地給出這類無窮數列的一個通項公式。
無窮數列
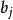無窮數列
無窮數列將無理數α表示成無限不循環小數，(其中、為0～ 9中的數字,a1≠ 0，j= 1,2,3,…)，依次取α的精確到個位,十分位,百分位,千分位,…的不足近似值：
無窮數列
無窮數列
無窮數列一般地，其中{x}表示x的小數部分)。
無窮數列
無窮數列類似地，我們容易推得無理數α精確到個位、十分位、百分位、千分位…的過剩近似值構成的數列的一個通項公式為:(其中{x}表示x的小數部分)。
