定義
已知函式定義域被分成有限個區間,若在各個區間上表示對應規則的數學表達式一樣,但單獨定義各個區間公共端點處的函式值;或者在各個區間上表示對應規則的數學表達式不完全一樣,則稱這樣的函式為分段函式。
其中定義域所分成的有限個區間稱為分段區間,分段區間的公共端點稱為分界點。
類型
1、分界點左右的數學表達式一樣,但單獨定義分界點處的函式值(例1)
2、分界點左右的數學表達式不一樣(例2)
 分段函式
分段函式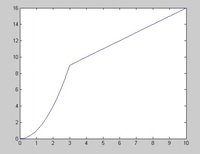 分段函式
分段函式 分段函式
分段函式例子
例一
某商場舉辦有獎購物活動,每購100元商品得到一張獎券,每1000張獎券為一組,編號為1號至1000號,其中只有一張中特等獎,特等獎金額5000元,開獎時,中特等獎號碼為328號,那么,一張獎券所得特等獎金y元與號碼x號的函式關係表示為
0 ,x≠328
y={ 5000, x=328
例二
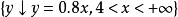 分段函式
分段函式某商店賣西瓜,一個西瓜的重量若在4kg以下,則銷售價格為0.6元/kg;若在4kg 或4kg 以上,則銷售價格為0.8元/kg,那么,一個西瓜的銷售收入y元與重量xkg的函式關係表示為
,
;
分段函式題型
由於課本沒有明確給出分段函式的定義,只以例題的形式出現,不少學生對它認識膚淺模糊,以致學生解題常常出錯。本段介紹分段函式的若干種題型及其解法,以供大家參考。
作圖題
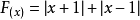 分段函式
分段函式例1作出函式
的圖像。
分析:(根據北師大版32頁例題2)
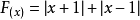 分段函式
分段函式函式去絕對值符號後就變為分段函式
f(x)=|x+1|+|x-1| =
這個分段函式有三段,所以這個函式的圖像應由三條線組成,其中兩邊各是一條射線,中間是一條線段。
分段函式作圖題的一般解法:分段函式有幾段它的圖像就由幾條曲線組成,作圖的關鍵就是根據每段函式的定義區間和表達式在同一坐標系中作出其圖像,作圖時要注意每段曲線端點的虛實,而且橫坐標相同之處不可有兩個以上的點。
求函式值
例2已知函式f(x)= 求f(3)的值。
解:由3∈(-∞,6),知f(3)=f(3+2)=f(5),
又5∈(-∞,6),所以f(5)=f(5+2)=f(7).
又由7∈[6,+∞)所以f(7)=7-2=5,因此,f(3)=5。
求分段函式的函式值的方法:先確定要求值的自變數屬於哪一段區間,然後按該段的表達式去求值,直到求出值為止。
求函式值域
例3求函式f(x)= 的值域。
解:當-2≤x≤a時,x2 的取值有三種情形:
(1)當-2≤a<0時,有a2≤x2≤4 ;
(2)當0≤a≤2時,有0≤x2≤4 ;
(3)當a>2時,有0≤x2≤a2
當x>a時,-|x|的取值有兩種情形:
(1)當-2≤a<0時,有-|x|≤0,
(2)當a≥0時,有-|x|<-a 。
所以原函式的值域為:
(1)當-2≤a<0時,為(-∞,0]∪[a2,4] ;
(2)當0≤a≤2時,為(-∞,-a)∪[0,4];
(3)當a>2時,為(-∞,-a)∪[0,a2]
求分段函式的值域的方法:分別求出各段函式在其定義區間的值域,再取它們的並集即可。
函式的奇偶性
例4 判斷下列函式的奇偶性
(1)f(x)= (2)f(x)=
解:(1)∵當x>0時,-x<0, f(x)=ex ,f(-x)=-e-(-x) =-ex ,
即有f(x)=-f(-x),同理,當x<0時,也有f(x)=-f(-x)
∴函式f(x)是奇函式。
(2)∵當x=0時,f(0)=f(-0)=0 ,
當x>0時,-x<0,f(x)=x(1-x) ,f(-x)=-(-x)[1+(-x)]=x(1-x) ,
即有f(x)=f(-x),同理,當x<0時,也有f(x)=f(-x).
∴函式f(x)是偶函式。
判斷分段函式的奇偶性的方法:先看定義域是否關於原點對稱,不對稱就不是奇(偶)函式,再由x>0,-x<0 ,分別代入各段函式式計算f(x)與f(-x)的值,若有f(x)=-f(-x),當x=0有定義時f(0)=0,則f(x)是奇函式;若有f(x)=f(-x),則f(x)是偶函式。
函式的單調性
例5 討論函式f(x)= 的單調性。
解:當x≥0時,f(x)=-x2+4x-10 ,它是開口向下,對稱軸為x=2的拋物線的一部分,因此f(x)在區間[0,2]上是增加的,在區間(2,+∞)上是減少的;當x<0時,f(x)=-x2-4x-10 ,它是開口向下,對稱軸為x=-2的拋物線的一部分,因此f(x)在區間[-2,0)上是減少的,在區間(-∞,-2)上是增加的。
分段函式的單調性的判斷方法:分別判斷出各段函式在其定義區間的單調性即可。
求函式的最小正周期
求分段函式的最小正周期的方法有:定義法、公式法和作圖法。
例6 求函式f(x)= 的最小正周期。
定義法:當x=2kπ或2kπ+π時,sin(2kπ+π)=sin2kπ=0
當2kπ-π<2kπ時,2kπ<2kπ+π,k∈z
f(x)=-sinx ,f(x+π)=sin(x+π)=-sinx ,
即有f(x+π)=f(x) ,同理可證:當2kπ<2kπ+π (k∈z)時,
有f(x+π)=f(x) ,所以f(x) 的最小正周期是π。
公式法:∵(2kπ-π,2kπ)∪[2kπ,2kπ+π]=R , (k∈z)
x∈(2kπ-π,2kπ),sinx <0 ,x∈[2kπ,2kπ+π],sinx ≥0 .
∴f(x)=|sinx|= =
所以f(x) 的最小正周期T= =π
作圖法:作出函式f(x)的圖像如圖2
所示。
由圖2知f(x) 的最小正周期是π。 圖2
求函式的最大(小)值
求函式的最大(小)值的方法有:
數形結合法、分析綜合法。
例7 求函式f(x)= 的最大和最小值。
解:∵函式f(x)=log2 x 在[1,8]是增加的,最大值是f(8)=3,
最小值是f(1)=0。又∵函式f(x)=x+2 在[-8,1)是增加的,最小值是f(-8)=-6且f(x)<3。
∴綜上,得函式f(x) 的最大值是3 ,最小值是-6。
求某條件下自變數的範圍
例8 函式f(x)=
若f(x0)<-3則x0取值範圍是______.
解:(1)當x0≤-2時,f(x)=x0<-3 , 此時不等式的解集是
(-∞,-3) ;
(2)當-2<4時,f(x0)=x<-3 ,此時不等式的解集是 ;
(3)當x0≥4時,f(x0)=3x0 <-3 , 此時不等式的解集是 .
所以則x0的取值範圍是(-∞,-3)。
求某條件下自變數的範圍的方法:先假設所求的解在分段函式定義域的各段上,然後相應求出在各段定義域上的範圍,再求它們並集即可。
求自變數的值
例9 已知函式f(x)= ,若f(a)=2 ,則實數a的值是______.
解:(1)當a≤-3時,f(a)=3a =2 ,3a ≤3= ,此時方程無解;
(2)當-3<4時,f(a)= a+4 =2 ,解得 a=-2
(3)當a≥4時,f(a)= =2 ,解得 a=4 ,
∴實數a的值是a=-2 或a=4 。
求某條件下自變數的值的方法:先假設所求的解在分段函式定義域的各段上,然後相應求出在各段定義域上的解,再求它們的並集即可。
求函式的表達式
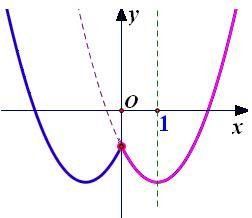
例10 求二次函式f(x)=x2-2(2a-1)x+5a2-4a+2在[0,1]上的最小值g(a)的解析式。
解:二次函式f(x)=x2-2(2a-1)x+5a2-4a+2=[x-(2a-1)]2+a2+1
圖像開口向上,對稱軸是x=2a-1 .
(1)若2a-1<0即a< 時,如圖10-1所示
二次函式f(x)在[0,1]上的最小值是
g(a)=f(0)=5a2-4a+2 ;
(2)若0≤2a-1<1即 ≤a<1時,如圖10-2所示
二次函式f(x)在[0,1]上的最小值是
g(a)=f(2a-1)=a2+1;
(3)若2a-1≥1即a≥1時,如圖10-3所示
二次函式f(x)在[0,1]上的最小值是
g(a)=f(1)=1-2(2a-1)+5a2-4a+2
=5a2-8a+5 .
綜上所述,二次函式f(x)在[0,1]上的最小值是
g(a)=
求分段函式的表達式的常用方法有:待定係數法、數形結合法和公式法等。本題採用數形結合法。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |