正整數集:正整數集，即所有正數且是整數的數的集合。在數學中，有正數和負數 -百科知識中文網

正整數集

正整數集，即所有正數且是整數的數的集合。在數學中，有正數和負數之分，用數軸表示，起點為原點0，箭頭指向方向（一般為右邊）的為正數，箭頭反向（一般為左邊）的為負數；而集代表的是所有，正整數集即在自然數集中排除0的集合，一直到無窮大。

分類

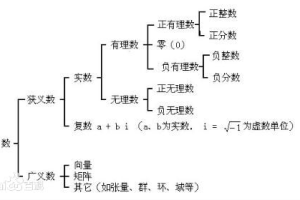
有理數可以分為:正有理數、負有理數、0。其中，正有理數包括:正整數、正分數。負有理數包括:負分數、負整數。有理數可以分為:分數和整數。其中，整數包括:正整數、負整數、0。分數包括:正分數、負分數。

正整數集可以用符號N+、N*、N1、N>0表示。其中，N表示自然數集，Z表示整數集，+表示該數集中的元素都為正數，*表示在剔除該數集的元素0（例如，R*表示剔除R中元素0後的數集。即R*=R\{0}=R-∪R+=（-∞，0）∪（0，+∞）。）。

所有正整數組成的集合稱為正整數集，記作N*，Z+或N+；

非負整數組成的集合稱為非負整數集（或自然數集），記作N；

整數組成的集合稱為整數集，記作Z；

有理數組成的集合稱為有理數集，記作Q；

實數組成的集合稱為實數集，記作R；全體虛數組成的集合稱為虛數集，記作I；

實數和虛數組成的複數的集合稱為複數集，記作C。

請將:-42、-74、-85、-37、-34、16、4、52、48、58分類。

正整數集合:{16、4、52、48、58……}

負整數集合:{-42、-74、-85、-37、-34……}