表示方法
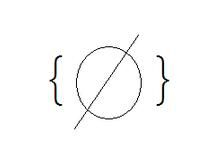 空集
空集注意:{Ø}為有一個Ø(oe)元素的集合,而不是空集。
舉例
當兩圓相離時,它們的公共點所組成的集合就是空集;當一元二次方程的根的判別式值小於0時,它的實數根所組成的集合也是空集。
常見問題
空集不是無;它是內部沒有元素的集合,而集合就是有。這通常是初學者的一個難點。將集合想像成一個裝有其元素的袋子的想法或許會有幫助;袋子可能是空的,但袋子本身確實是存在的。
有些人會想不通上述第一條性質,即空集是任意集合A的子集。按照子集的定義,這條性質是說 { } 的每個元素x都屬於A。若這條性質不為真,那 { } 中至少有一個元素不在A中。由於{ }中沒有元素,也就沒有{ }的元素不屬於A了,得到{ }的每個元素都屬於 A, 即{ }是A的子集。
公理集合論
在諸如策梅羅-弗蘭克爾集合論的公理集合論中,空集的存在性是由空集公理確定的。空集的唯一性由 外延公理得出。
使用分離公理,任何陳述集合存在性的公理將隱含 空集公理。例如:若 A 是集合,則分離公理允許構造集合B={x in A | x ≠ x},它就可以被定義為空集。
空集的運算
空集(作為集合)上的運算也可能使人迷惑。(這是一種空運算。)例如:空集元素的和為0,而它們的積為1(見空積)。這可能看上去非常奇怪,空集中沒有元素,最終,這些運算的結果更多被看成是運算的問題,而不是空集的。比如,可以注意到0是加法的單位元,而1是乘法的單位元。
範疇論
若A為集合,則恰好存在從{ }到A的函式f,即空函式。結果,空集是集合和函式的範疇的唯一初始對象。
空集只能通過一種方式轉變為拓撲空間,即通過定義空集為開集;這個空拓撲空間是有連續映射的拓撲空間的範疇的唯一初始對象。
空集是任何非空集合的真子集。
Ø只有一個子集,沒有真子集。{Ø}有兩個子集,一個是Ø一個是它本身。
定義:
不含任何元素的集合稱為空集。
A={1,2,3,4,5} B={1,3,5} c={5,4,3,2,1}
例如,“B是A的子集”,意思是B的任何一個元素都是A的元素,即由任一 ,可以推出 ,但不能把B是A的子集解釋成B是由A中部分元素所組成的集合.因為B的子集也包括它本身,而這個子集是由B的全體元素組成的.
空集也是B的子集,而這個集合中並不含有B中的元素.由此也可看到,把B是A的真子集解釋成B是由A的部分元素組成的集合也是不確切的.正確的說法應該把真子集的兩個特徵:“B是A的子集”和“A中至少有一個元素不屬於B都指出.
“空集是任何集合的子集”這句話是正確的,但是把空集說成是任何集合的真子集就不確切.因為空集是它本身的子集.正確的說法是“空集是任何非空集合的真子集”.總之,對於概念的解釋,語言表達必須確切.
再如,“ AB是A在全集B中的補集”,不能把它簡單地說成 AB是A的補集,因為補集的概念是相對而言的,集合A在不同的全集中的補集是不同的,所以在描述補集概念時,一定要註明是在哪個例如,屬於符號“∈ ”、不屬於符號“∉”,它們只能用在元素與集合符號之間;包含於(被包含)符號“⊆ ”、包含
符號“⊇”,它們只能用在兩個集合符號之間.對此,必須引起學生充分注意,不能用錯,不要出現把a∈{a}表示成a⊆{a},或a⊇{a}之類的錯誤。
又如,{0}是含有一個元素的集合,Ø是不含任何元素的集合,因此,有Ø⊆{0},不能寫成Ø={0} 或Ø∈{0}。
關於子集與真子集的記法,教科書中採用的是新的國家標準,與原教科書不盡相同,應該注意。
關於補集,新的國家標準規定,集合A中子集B的補集或余集記為C B ,如果行文中集合A已經很明確,則常常可以省去符號A,而記為C B。
集合中的補集,簡單的說集合A的補集是沒有意義的。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |

