介紹
數論函式的一種,其定義域與值域都是自然數集,只是由於構作函式方法的不同而有別於其他的函式。處處有定義的函式叫做全函式，未必處處有定義的函式叫做部分函式。最簡單又最基本的函式有三個:零函式O(x)=0(其值恆為0);射影函式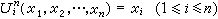
；後繼函式S(x)=x+1。它們合稱初始函式。要想由舊函式作出新函式，必須使用各種運算元。 代入（又名複合或疊置）是最簡單又最重要的造新函式的運算元，其一般形狀是：由一個m元函式ƒ與m個n元函式 g1,g2,…,gm 造成新函式 ƒ (g1(x1,x2,…,xn)，g2(x1,x2,…,xn),…,gm(x1,x2，…，xn)),亦可記為ƒ(g1，g2,…,gm)(x1，x2,…,xn)。另一個造新函式的運算元是原始遞歸式。具有n個參數u1，u2,…,un的原始遞歸式為：
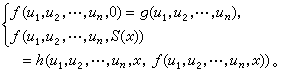
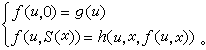
由初始函式出發，經過有限次的代入與原始遞歸式而作出的函式叫做原始遞歸函式。由於初始函式顯然是全函式且可計算，故原始遞歸函式都是全函式且可計算。通常使用的數論函式全是原始遞歸函式，可見原始遞歸函式是包括很廣的。但是W.阿克曼證明了，可以作出一個可計算的全函式，它不是原始遞歸的。經過後人改進後，這個函式可寫為如下定義的阿克曼函式：
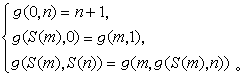
另一個重要的造新函式的運算元是造逆函式的運算元，例如，由加法而造減法，由乘法造除法等。一般，設已有函式ƒ(u,x),就x解方程ƒ(u,x)=t,可得x=g(u,t)。這時函式g叫做ƒ的逆函式。至於解一般方程ƒ(u，t,x)=0而得x＝g(u，t)可以看作求逆函式的推廣。解方程可以看作使用求根運算元。ƒ(u,t，x)=0的最小x根（如果有根的話），記為μx【ƒ(u,t,x)=0】。當方程沒有根時,則認為μx【ƒ(u,t,x)=0】沒有定義。可見,即使ƒ(u,t,x)處處有定義且可計算,但使用求根運算元後所得的函式μx【ƒ(u,t,x)=0】仍不是全函式,可為部分函式。但只要它有定義，那就必然可以計算。這運算元稱為μ運算元。如果ƒ(u,t,x)本身便是部分函式，則 μx【ƒ(u,t,x)=0】的意義是：當ƒ(u,t,n)可計算且其值為0,而x<n時ƒ(u,t,x)均可計算而其值非0，則 μx【ƒ(u,t,x)=0】指n；其他情況則作為無定義。例如，如果ƒ(u,t,x)=0根本沒有根，或者雖然知道有一根為n，但ƒ(u,t,n-1)不可計算,那么 μx【ƒ(u,t,x)=0】都作為沒有定義。在這樣定義後,只要 μx【ƒ(u,t,x)=0】有值便必可計算。由初始函式出發,經過有窮次使用代入、原始遞歸式與 μ運算元而作成的函式叫做部分遞歸函式，處處有定義的部分遞歸函式稱為全遞歸函式，或一般遞歸函式。
原始遞歸函式類里還有一個重要的子類稱為初等函式類,它是由非負整數與變元經過有窮次加、算術減（即｜α-b｜）、乘、算術除
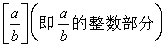、疊加Σ、疊乘П而得的函式組成的類。 波蘭人A.格熱高契克把原始遞歸函式類按定義的複雜程度來分類，稱為格熱高契克分層或波蘭分層。
要把遞歸函式套用於謂詞，首先要定義謂詞的特徵函式。謂詞R(x,y)的特徵函式是
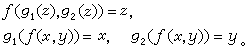
可以構造許多原始遞歸的配對函式。
遞歸函式也可以用來處理符號串。處理的辦法是對符號及符號串配以自然數。這方法是K.哥德爾開始引進的，因此稱為哥德爾配數法。例如，在要處理的符號系統｛α1，α2，α3,…｝中，可以用奇數1，3，5，7，…作為α1,α2，α3，α4，…的配數，符號串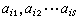
以
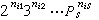為其配數,其中Ps是第s個素數,nij是αij的配數。這種配數稱為哥德爾配數。有了哥德爾配數法，就可以用遞歸函式來描寫、處理有關符號串的謂詞了。
計算
數論函式的一種，其定義域與值域都是自然數集，只是由於構作函式方法的不同而有別於其他的函式。處處有定義的函式叫做全函式，未必處處有定義的函式叫做部分函式。最簡單又最基本的函式有三個：零函式O（x）=0（其值恆為0）；射影函式；後繼函式S（x）=x+1。它們合稱初始函式。要想由舊函式作出新函式，必須使用各種運算元。代入（又名複合或疊置）是最簡單又最重要的造新函式的運算元，其一般形狀是：由一個m元函式？與m個n元函式g1,g2,…，gm造成新函式?（g1（x1,x2,…，xn），g2（x1,x2,…，xn），…，gm（x1,x2，…，xn）），亦可記為？（g1，g2,…，gm）（x1，x2,…，xn）。另一個造新函式的運算元是原始遞歸式。具有n個參數u1，u2,…，un的原始遞歸式為：（圖1）
具有一個參數的原始遞歸式可簡寫為：（圖2）
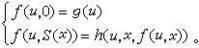遞歸函式1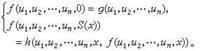
遞歸函式2其特點是，不能由g、h兩函式直接計算新函式的一般值？（u,x），而只能依次計算？（u,0），？（u,1），？（u,2），…；但只要依次計算，必能把任何一個？（u,x）值都算出來。換句話說?只要g,h為全函式且可計算，則新函式f也是全函式且可計算。由初始函式出發，經過有限次的代入與原始遞歸式而作出的函式叫做原始遞歸函式。由於初始函式顯然是全函式且可計算，故原始遞歸函式都是全函式且可計算。通常使用的數論函式全是原始遞歸函式，可見原始遞歸函式是包括很廣的。但是W.阿克曼證明了，可以作出一個可計算的全函式，它不是原始遞歸的。經過後人改進後，這個函式可寫為如下定義的阿克曼函式：（圖3）
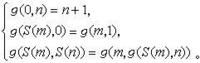遞歸函式3容易看出，這個函式是處處可計算的。任給m,n的值，如果m為0，可由第一式算出；如果m不為0而n為0，可由第二式化歸為求g（m,1）的值，這時第一變目減少了；如果m，n均不為0,根據第三式可先計算g（m,n-1），設為α，再計算g（m-1,α），前者第二變目減少（第一變目不變），後者第一變目減少。極易用歸納法證得，這樣一步一步地化歸，最後必然化歸到第一變目為0，從而可用第一式計算。所以這個函式是處處可計算的。此外又容易證明，對任何一個一元原始遞歸函式？（x），永遠可找出一數α使得？（x）<g（α，x）。這樣，g（x,x）+1便不是原始遞歸函式，否則將可找出一數b使得g（x,x）+1<g（b,x）。令x=b，即得g（b,b）+1<g（b,b），而這是不可能的。
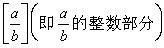遞歸函式4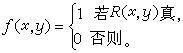
遞歸函式5
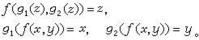遞歸函式6可見，即使？（u,t,x）處處有定義且可計算，但使用求根運算元後所得的函式μx【？（u,t,x）=0】仍不是全函式，可為部分函式。但只要它有定義，那就必然可以計算。這運算元稱為μ運算元。如果？（u,t,x）本身便是部分函式，則μx【？（u,t,x）=0】的意義是：當？（u,t,n）可計算且其值為0,而x<n時？（u,t,x）均可計算而其值非0，則μx【？（u,t,x）=0】指n；其他情況則作為無定義。例如，如果？（u,t,x）=0根本沒有根，或者雖然知道有一根為n，但？（u,t,n-1）不可計算，那么μx【？（u,t,x）=0】都作為沒有定義。在這樣定義後，只要μx【？（u,t,x）=0】有值便必可計算。由初始函式出發，經過有窮次使用代入、原始遞歸式與μ運算元而作成的函式叫做部分遞歸函式，處處有定義的部分遞歸函式稱為全遞歸函式，或一般遞歸函式。
原始遞歸函式類里還有一個重要的子類稱為初等函式類，它是由非負整數與變元經過有窮次加、算術減（即｜α-b｜）、乘、算術除（圖2）、疊加Σ、疊乘П而得的函式組成的類。
波蘭人A.格熱高契克把原始遞歸函式類按定義的複雜程度來分類，稱為格熱高契克分層或波蘭分層。要把遞歸函式套用於謂詞，首先要定義謂詞的特徵函式（圖6）
。謂詞R（x,y）的特徵函式是（圖4）：
稱謂詞R是遞歸謂詞，若R的特徵函式是遞歸函式；稱自然數子集A為遞歸集，若謂詞x∈A是遞歸謂詞。有了上述定義，就可以用遞歸函式來處理遞歸謂詞和遞歸集。為了處理N×N（其中N為自然數集）的子集，就要建立配對函式，所謂配對函式通常是指由N×N到N的一個函式？（x，y）與它的逆函式g1（z），g2（z）。它們都滿足以下關係：（圖5）
可以構造許多原始遞歸的配對函式。
遞歸函式也可以用來處理符號串。處理的辦法是對符號及符號串配以自然數。這方法是K.哥德爾開始引進的，因此稱為哥德爾配數法。例如，在要處理的符號系統｛α1，α2，α3,…｝中，可以用奇數1，3，5，7，…作為α1,α2，α3，α4，…的配數，為其配數，其中Ps是第s個素數，nij是αij的配數。這種配數稱為哥德爾配數。有了哥德爾配數法，就可以用遞歸函式來描寫、處理有關符號串的謂詞了。
運用
C++語言
(一)
目的：將1號和2號從A移到B
調用函式：hanoi(2,'A','C','B')。
在hanoi(2,'A','C','B')中遞歸調用如下：
A-->C----hanoi(1,'A','B','C')
A-->B----hanoi(1,'A','C','B')
C-->B----hanoi(1,'C','A','B')
(二)
目的：將3號從A移到C
調用函式：hanoi(1,'A','B','C')
A-->C
(三)
目的：將1號和2號從B移到C
調用函式：hanoi(2,'B','A','C')
在hanoi(2,'B','A','C')中遞歸遞歸如下：
B-->A----hanoi(1,'B','C','A')
B-->C----hanoi(1,'B','A','C')
A-->C----hanoi(1,'A','B','C')
總共調用了7次函式，
只要hanoi()的第一個參數大於1，它就會在內部調用自身3次，“直到第一個參數＝1，然後調用printf()”。
hanoi(n,...)調用hanoi(1,...)的次數為2的n次方減去一。
【pascal語言】
functiondo(x:integer);
begin
ifx<=1thenexit(0)
elseifx>1thenexit(do(x-1)+10)
end;
【C++語言】用遞歸法計算1+2+。。。N的值。
#include<iostream.h>
intfn(inti);
voidmain()
{
intN;
cout<<"\n輸入一個正整數:";
cin>>N;
cout<<"\n1+2+...+"<<N<<"的結果是:"<<fn(N)<<"\n";
} //遞歸函式的定義
intfn(inti)
{
if(i==1)
return1;
else
returni+fn(i-1);
}
正確寫出如何快速正確的寫出遞歸函式？寫一個遞歸函式是非常程式化的東西，只要按照一定的規則來寫，就可以很容易地寫出遞歸函式。寫遞歸函式有三步：
①寫出疊代公式；
②確定遞歸終止條件；
③將①②翻譯成代碼。以求n！為例：
①寫出疊代公式：n！的疊代公式為
②確定遞歸終止條件：1！＝1就是遞歸終止條件
③將①②翻譯成代碼：將疊代公式等號右邊的式子寫入return語句中，即return（fact（n-1））*n;將1！＝1翻譯成判斷語句：if（n==1）return1;按照先測試，後遞歸的原則寫出代碼。longfact（intn）{if（n==1）return1;return（fact（n-1））*n;}下面再舉一個例子，希望能幫助大家進一步體會這一原則
寫一個函式，求：f（n）=1+2+3+……+n的值
①寫出疊代公式：疊代公式為②確定遞歸終止條件：f（1）＝1就是遞歸終止條件
③將①②翻譯成代碼：將疊代公式等號右邊的式子寫入return語句中，即return（Sum（n-1））+n;將1！＝1翻譯成判斷語句：if（n==1）return1;按照先測試，後遞歸的原則寫出代碼。longSum（intn）{if（n==1）return1;return（Sum（n-1））+n;}
Oracle用法
Oraclestartwithconnectby用法
oracle中connectbyprior遞歸算法
Oracle中startwith...connectbyprior子句用法connectby是結構化查詢中用到的，其基本語法是：
select...fromtablenamestartwith條件1
connectby條件2
where條件3;
例：
select*fromtable
startwithorg_id='HBHqfWGWPy'
connectbypriororg_id=parent_id;
簡單說來是將一個樹狀結構存儲在一張表里，比如一個表中存在兩個欄位:
org_id,parent_id那么通過表示每一條記錄的parent是誰，就可以形成一個樹狀結構。
用上述語法的查詢可以取得這棵樹的所有記錄。
其中：
條件1是根結點的限定語句，當然可以放寬限定條件，以取得多個根結點，實際就是多棵樹。
條件2是連線條件，其中用PRIOR表示上一條記錄，比如CONNECTBYPRIORorg_id=parent_id就是說上一條記錄的org_id是本條記錄的parent_id，即本記錄的父親是上一條記錄。
條件3是過濾條件，用於對返回的所有記錄進行過濾。
簡單介紹如下：
早掃描樹結構表時，需要依此訪問樹結構的每個節點，一個節點只能訪問一次，其訪問的步驟如下：
第一步：從根節點開始；
第二步：訪問該節點；
第三步：判斷該節點有無未被訪問的子節點，若有，則轉向它最左側的未被訪問的子節，並執行第二步，否則執行第四步；
第四步：若該節點為根節點，則訪問完畢，否則執行第五步；
第五步：返回到該節點的父節點，並執行第三步驟。
總之：掃描整個樹結構的過程也即是中序遍歷樹的過程。
