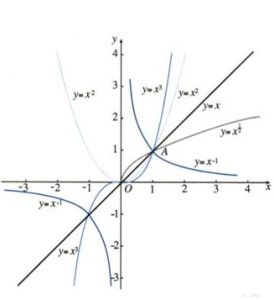
概念
形如y=x^a(a為常數)的函式,即以底數為自變數,冪為因變數,指數為常量的函式稱為冪函式。當a取非零的有理數時是比較容易理解的,而對於a取無理數時,初學者則不大容易理解了。因此,在初等函式里,我們不要求掌握指數為無理數的問題,只需接受它作為一個已知事實即可,因為這涉及到實數連續性的極為深刻的知識。
性質
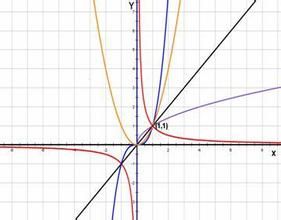 冪函式
冪函式(1)當α>0時,冪函式y=xa有下列性質:
a、圖像都通過點(1,1)(0,0);
b、在第一象限內,函式值隨x的增大而增大;
c、在第一象限內,α>1時,圖像開口向上;0<α<1時,圖像開口向右;
d、函式的圖像通過原點,並且在區間[0,+∞)上是增函式。
(2)當α<0時,冪函式y=xa有下列性質:
a、圖像都通過點(1,1);
b、在第一象限內,函式值隨x的增大而減小,圖像開口向上;
c、在第一象限內,當x從右趨於原點時,圖像在y軸上方趨向於原點時,圖像在y軸右方無限接近y軸,當x趨於+∞時,圖象在x軸上方無限地逼近x軸。
(3)當α=0時,冪函式y=xa有下列性質:
a、y=x0是直線y=1去掉一點(0,1)它的圖像不是直線。
特性
對於a的取值為非零有理數,有必要分成幾種情況來討論各自的特性:
首先我們知道如果a=p/q,且p/q為既約分數(即p、q互質),q和p都是整數,則x^(p/q)=q次根號下(x的p次方),如果q是奇數,函式的定義域是R,如果q是偶數,函式的定義域是[0,+∞)。當指數a是負整數時,設a=-k,則y=1/(x^k),顯然x≠0,函式的定義域是(-∞,0)∪(0,+∞)。因此可以看到x所受到的限制來源於兩點,一是有可能作為分母而不能是0,一是有可能在偶數次的根號下而不能為負數,那么我們就可以知道:
a小於0時,x不等於0;
a的分母為偶數時,x不小於0;
a的分母為奇數時,x取R。
定義域和值域
當a為不同的數值時,冪函式的定義域的不同情況如下:
1、如果a為負數,則x肯定不能為0,不過這時函式的定義域還必須根據q的奇偶性來確定,即如果同時q為偶數,則x不能小於0,這時函式的定義域為大於0的所有實數;
2、如果同時q為奇數,則函式的定義域為不等於0的所有實數。
當x為不同的數值時,冪函式的值域的不同情況如下:
1、在x大於0時,函式的值域總是大於0的實數。
2、在x小於0時,則只有同時q為奇數,函式的值域為非零的實數。
而只有a為正數,0才進入函式的值域。
由於x大於0是對a的任意取值都有意義的,
因此下面給出冪函式在第一象限的各自情況。
特殊性
可以看到:
(1)所有的圖形都通過(1,1)這點,(a≠0)a>0時圖象過點(0,0)和(1,1)
(2)單調區間:
當a為整數時,a的正負性和奇偶性決定了函式的單調性:
①當a為正奇數時,圖像在定義域為R內單調遞增;
②當a為正偶數時,圖像在定義域為第二象限內單調遞減,在第一象限內單調遞增;
③當a為負奇數時,圖像在第一三象限各象限內單調遞減(但不能說在定義域R內單調遞減);
④當a為負偶數時,圖像在第二象限上單調遞增,在第一象限內單調遞減。
當a為分數時,a的正負性和分母的奇偶性決定了函式的單調性:
①當a>0,分母為偶數時,函式在第一象限內單調遞增;
②當a>0,分母為奇數時,函式在第一三象限各象限內單調遞增;
③當a<0,分母為偶數時,函式在第一象限內單調遞減;
④當a<0,分母為奇數時,函式在第一三象限各象限內單調遞減(但不能說在定義域R內單調遞減);
(3)當a>1時,
冪函式圖形下凸(豎拋);當0<a<1時,冪函式圖形上凸(橫拋)。當a<0時,圖像為雙曲線。
(4)在(0,1)上,冪函式中a越大,函式圖像越靠近x軸;在(1,﹢∞)上冪函式中a越大,函式圖像越遠離x軸。
(5)當a<0時,a越小,圖形傾斜程度越大。
(6)顯然冪函式無界限。
(7)a=2n,該函式為偶函式{x|x≠0}。
圖象
冪函式冪函式的圖象:
①當a≤-1且a為奇數時,函式在第一、第三象限為減函式
②當a≤-1且a為偶數時,函式在第二象限為增函式
③當a=0且x不為0時,函式圖象平行於x軸且y=1、但不過(0,1)
④當0<a<1時,函式是增函式
⑤當a≥1且a為奇數時,函式是奇函式
⑥當a≥1且a為偶數時,函式是偶函式
冪函式的圖像不過第四象限
特別說明
為了研究方便,在初等函數裡對於冪函式,只討論a=1,2,3,1/2,-1時的情形。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |