定理內容
在任意△ABC中，角A、B、C所對的邊長分別為a、b、c，三角形外接圓的半徑為R，直徑為D。則有：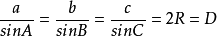
一個三角形中，各邊和所對角的正弦之比相等，且該比值等於該三角形外接圓的直徑（半徑的2倍）長度。
定理證明
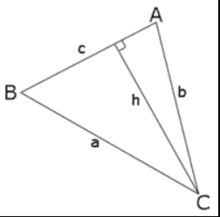
很明顯：
和
因此：
和
同理：
證明二：外接圓
①銳角三角形中
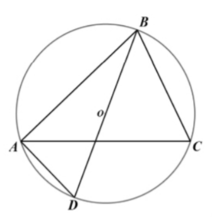
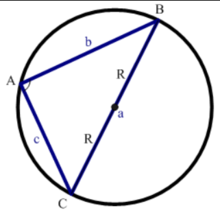
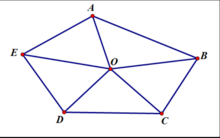
如圖，作△ABC的外接圓，O為圓心。連結BO並延長交圓於D， 設BD=2R。根據直徑所對圓周角是直角及同弧所對圓周角相等，可得:∠DAB=90°，∠C=∠D。
∴
，∴
。同理可證
,
。∴
。②直角三角形中
因為BC =a= 2R，可以得到
所以可以證明
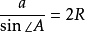
③鈍角三角形中
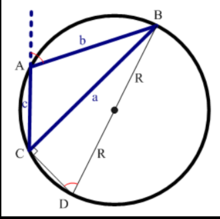
線段BD是圓的直徑 根據圓內接四邊形對角互補的性質
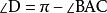
所以
因為BD為外接圓的直徑BD = 2R。根據正弦定義
變形可得
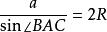
根據以上的證明方法可以證明得到得到三角形的一條邊與其對角的正弦值的比等於外接圓的直徑，即
證明三：向量
若△ABC為銳角三角形,過點A作單位向量j⊥
,則j與
的夾角為90°-∠A,j與
的夾角為90°-∠C.由向量的加法原則可得
為了與圖中有關角的三角函式建立聯繫,我們在上面向量等式的兩邊同取與向量j的數量積運算,得到
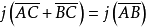
∴|j| |
|Cos90°+|j| |
|Cos(90°-C)=|j| |
|Cos(90°-A)
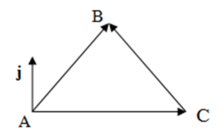
.∴asinC=csinA 即
同理,過點C作與
垂直的單位向量j,則j與
的夾角為90°+∠C,j與的夾角為90°+∠B,可得
若△ABC為鈍角三角形,不妨設A>90°,過點A作與AB垂直的單位向量j,則j與AC的夾角為∠A-90°,j與CB的夾角為90°+∠B.同理
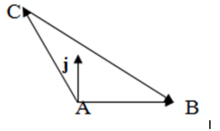
a·Cos(90°-B)=b·Cos(A-90°),
∴asinB=bsinA 即
過點C作與
垂直的單位向量j,則j與的夾角為90°+∠C,j與的夾角為90°+∠B,可得綜上，
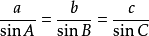。公式變形
△ABC中，若角A，B，C所對的邊為a，b，c，三角形外接圓半徑為R，直徑為D，正弦定理進行變形有
1.
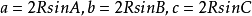
2.
,
,
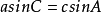
3.
4.
（等比，不變）
5.
（三角形面積公式）
三面角正弦定理
若三面角的三個面角分別為α、β、γ，它們所對的二面角分別為A、B、C,則
定理意義
正弦定理指出了任意三角形中三條邊與對應角的正弦值之間的一個關係式。由正弦函式在區間上的單調性可知，正弦定理非常好地描述了任意三角形中邊與角的一種數量關係。
一般地，把三角形的三個角A、B、C和它們的對邊a、b、c叫做三角形的元素。已知三角形的幾個元素求其他元素的過程叫做解三角形。正弦定理是解三角形的重要工具。
實際套用
1、在解三角形中，有以下的套用領域：
已知三角形的兩角與一邊，解三角形。
已知三角形的兩邊和其中一邊所對的角，解三角形。
運用a:b:c=sinA:sinB:sinC解決角之間的轉換關係。
注意：
解三角形時，已知兩角與一邊，三角形是確定的，利用正弦定理解三角形時，其解是唯一的；已知三角形的兩邊和其中一邊的對角，由於該三角形具有不穩定性，所以其解不確定，可結合平面幾何作圖的方法及“大邊對大角，大角對大邊”定理和三角形內角和定理去考慮解決問題。
一般地，已知兩邊和其中一邊的對角解三角形，有兩解、一解、無解三種情況，可參考三角形性質、鈍角三角形性質進行判斷。若已知A、A的對邊a、A與a的夾邊C，則：
對於鈍角三角形，
若a≤b，則無解；
若a>b，則有一解；
對於銳角三角形，
若a
若a=bsinA，則有一解；
若bsinA
若a≥b，則有一解。
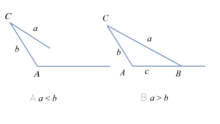鈍角三角形2、三角形面積的計算。
盤點高中數學名詞
| 高中是大學的過渡階段，學好高中數學，才能為學好大學數學打好基礎，那我們盤點下高中數學中有哪些名詞吧。 |
