名稱來源
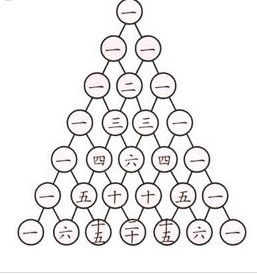
楊輝,字謙光,南宋時期杭州人。在他1261年所著的《詳解九章算法》一書中,輯錄了如上所示的數表,稱之 楊輝三角圖
楊輝三角圖而這樣一個三角在我們的奧數競賽中也是經常用到,最簡單的就是要找規律。
簡介
簡單的說,就是兩個未知數和的冪次方運算後的係數問題,比如(x+y)²=x²+2xy+y²,這樣係數就是1,2,1這就是楊輝三角的其中一行,立方,四次方,運算的結果看看各項的係數,你就明白其中的道理了。
這就是楊輝三角,也叫賈憲三角,在外國被稱為帕斯卡三角。他於我們現在的學習聯繫最緊密的是2項式乘方展開式的係數規律。如圖,在賈憲三角中,第3行的第三個數恰好對應著兩數和的平方公式(在此就不做說明了)依次下去。
性質
楊輝三角最本質的特徵是,它的兩條斜邊都是由數字1組成的,而其餘的數則是等於它肩上的兩個數之和。
其實,中國古代數學家在數學的許多重要領域中處於遙遙領先的地位。中國古代數學史曾經有自己光輝燦爛的篇章,而楊輝三角的發現就是十分精彩的一頁。楊輝,字謙光,北宋時期杭州人。在他1261年所著的《詳解九章算法》一書中,輯錄了如上所示的三角形數表,稱之為“開方作法本源”圖。而這樣一個三角在我們的奧數競賽中也是經常用到,最簡單的就是叫你找規律。現在要求我們用編程的方法輸出這樣的數表。
規律
這也是多項式(a+b)^n打開括弧後的各個項的二次項係數的律規
0(a+b)^0(0nCr0)
1(a+b)^1(1nCr0)(1nCr1)
2(a+b)^2(2nCr0)(2nCr1)(2nCr2)
3(a+b)^3(3nCr0)(3nCr1)(3nCr2)(3nCr3)
................
因此楊輝三角第x層第y項直接就是(ynCrx)
我們也不難得到第x層的所有項的總和為2^x(即(a+b)^x中a,b都為1的時候)
[上述y^x指y的x次方;(anCrb)指組合數]
其實,中國古代數學家在數學的許多重要領域中處於遙遙領先的地位。中國古代數學史曾經有自己光輝燦爛的篇章,而楊輝三角的發現就是十分精彩的一頁。
數字表示
楊輝三角是一個由數字排列成的三角形數表,一般形式如下:
1n=0
11n=1
121n=2
1331n=3
14641n=4
15101051n=5
1615201561n=6
與二項式定理的關係
楊輝三角的第n行就是二項式展開式的係數列。
對稱性:楊輝三角中的數字左、右對稱,對稱軸是楊輝三角形底邊上的“高”。
結構特徵:楊輝三角除斜邊上1以外的各數,都等於它“肩上”的兩數之和。
這些數排列的形狀像等腰三角形,兩腰上的數都是1。
從右往左斜著看,從左往右斜著看,和前面的看法一樣,這個數列是左右對稱的。
上面兩個數之和就是下面的一行的數。
這行數是第幾行,就是第二個數加一。
實際操作運用範例
這是“楊輝三角”的格式對於楊輝三角,很多國中生,甚至很多高中生只知道此三角中的某數等於它上排相鄰兩數之和,而忽視了楊輝三角的實際運用。
不難發現,除了上述特點外,楊輝三角還有另一個特點:
此數列中各行中的數字正好是二項式a+b乘方後,展開始終各項的係數。如:
(a+b)^1=a^1+b^1
(a+b)^2=a^2+2ab+b^2
(a+b)^3=a^3+3a^2b+3ab^2+b^3
……
(a+b)^6=a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6(注意發現規律)
……
如此一來,對於普通考試中所出現的高係數運算的展開運算,我們就不必因怕運算出錯而擔憂了。但這只是類似公式的技法,想要運算能力增強,還是一個一個拆著練吧。
另外,文章開頭提到的“賈憲三角”和“楊輝三角”是有區別的。只需將楊輝三角順時針鏇轉90度,便得到賈憲三角,如下:
11111111
7654321
211510631
35201041
351551
2161
71
1
這些數列,能有效地運用於解數字係數的高次方程。無論是在幾何、代數還是三角函式中,上述方法都能不同程度的提高解題效率。
[編輯本段]楊輝三角的前50行
第0行:
1
第1行:
11
第2行:
121
第3行:
1331
第4行:
14641
第5行:
15101051
第6行:
1615201561
第7行:
172135352171
第8行:
18285670562881
第9行:
193684126126843691
第10行:
1104512021025221012045101
第11行:
1115516533046246233016555111
第12行:
1126622049579292479249522066121
第13行:
11378286715128717161716128771528678131
第14行:
11491364100120023003343230032002100136491141
第15行:
11510545513653003500564356435500530031365455105151
第16行:
116120560182043688008114401287011440800843681820560120161
第17行:
1171366802380618812376194482431024310194481237661882380680136171
第18行:
118153816306085681856431824437584862043758318241856485683060816153181
第19行:
1191719693876116282713250388755829237892378755825038827132116283876969171191
第20行:
1201901140484515504387607752012597016796018475616796012597077520387601550448451140190201
第21行:
121210133059852034954264116280203490293930352716352716293930203490116280542642034959851330210211
第22行:
122231154073152633474613170544319770497420646646705432646646497420319770170544746132633473151540231221
第23行:
123253177188553364910094724515749031481719011440661352078135207811440668171904903142451571009473364988551771253231
第24行:
12427620241062642504134596346104735471130750419612562496144270415624961441961256130750473547134610413459642504106262024276241
第25行:
12530023001265053130177100480700108157520429753268760445740052003005200300445740032687602042975108157548070017710053130126502300300251
第26行:
1263252600149506578023023065780015622753124550531173577261609657700104006009657700772616053117353124550156227565780023023065780149502600325261
第27行:
1273512925175508073029601088803022200754686825843628513037895173838602005830020058300173838601303789584362854686825222007588803029601080730175502925351271
第28行:
1283783276204759828037674011840403108105690690013123110214741803042175537442160401166003744216030421755214741801312311069069003108105118404037674098280204753276378281
第29行:
1294063654237511187554750201560780429214510015005200300103459729051895935678639157755876077558760678639155189593534597290200300101001500542921451560780475020118755237513654406291
第30行:
13043540602740514250659377520358005852925143071503004501554627300864932251197598501454226751551175201454226751197598508649322554627300300450151430715058529252035800593775142506274054060435301
第31行:
1314654495314651699117362812629575788872520160075443521658467231514112052520625307526518252530054019530054019526518252520625307514112052584672315443521652016007578887252629575736281169911314654495465311
第32行:
13249649603596020137690619233658561051830028048800645122401290244802257928403473736004714356005657227206010803905657227204714356003473736002257928401290244806451224028048800105183003365856906192201376359604960496321
第33行:
13352854564092023733611075684272048138841563856710092561040193536720354817320573166440818809200103715832011668031101166803110103715832081880920057316644035481732019353672092561040385671001388415642720481107568237336409205456528331
第34行:
1345615984463762782561344904537961618156204524512561311281402860977605483540409279837601391975640185596752022039614302333606220220396143018559675201391975640927983760548354040286097760131128140524512561815620453796161344904278256463765984561341
第35行:
1355956545523603246321623160672452023535820706074601835793964172259008344518001476337800231995940032479431604059928950453756765045375676504059928950324794316023199594001476337800834451800417225900183579396706074602353582067245201623160324632523606545595351
第36行:
1366307140589053769921947792834768030260340941432802541868566008052961251677700231078960037962972005567902560730787211085974966009075135300859749660073078721105567902560379629720023107896001251677700600805296254186856941432803026034083476801947792376992589057140630361
第37行:
137666777066045435897232478410295472386080201244036203483301368549921521852482996356246730061070868009364199760128757746701590536871017672631900176726319001590536871012875774670936419976061070868003562467300185248299685499215234833013612440362038608020102954722324784435897660457770666371
第38行:138703843673815501942276068112620256489034921630116404727337561203322288270747514854149502969669554100154712865602223997443028781143380335780006103534526380033578000610287811433802223997443015471286560966955410054149502962707475148120332228847273375616301164048903492126202562760681501942738158436703381
第39行:
1397419139822515757573262623153809376152374821191513263574539616760560443910797436812242544415084504396251408406603771126099051021117810623591439906892326441068923264410623591439905102111781037711260990251408406601508450439681224254443910797436167605604463574539621191513261523748153809373262623575757822519139741391
第40行:
1407809880913906580083838380186435607690468527343888084766052823118014405586853480120332228802320692984040225345056628521016508873237880011338026180013128240840013784652882013128240840011338026180088732378800628521016504022534505623206929840120332228805586853480231180144084766052827343888076904685186435603838380658008913909880780401
第41行:
14182010660101270749398449638822481940955482453503435651121099408315946196878986549201762007636035240152720634322748961030774467061515844804502021126406002446626702002691289372202691289372202446626702002021126406001515844804501030774467066343227489635240152720176200763607898654920315946196811210994083503435659554824522481940449638874939810127010660820411
第42行:
142861114801119308506685245786269783281180301854458918101471442973428056137611058116888255187312805286022908098672427616166509721602254661927156353697121050446775310800513791607420538257874440513791607420446775310800353697121050254661927156166509721602986724276165286022908025518731280110581168884280561376147144297344589181011803018526978328524578685066811193011480
861421
第43行:
1439031234112341096259860964543222411414500851356392199519173347835752004349153386782643657684816878378960360151532656696265182149218421171648758608359048206800472431850960566918220105204948186010520494818609605669182208004724318506083590482064211716487582651821492181515326566967837896036036576848168153386782645752004349191733478356392199514500851332224114609645496259812341012341903431
第44行:
144946132441357511086008705905238320568177232627708930508248125677876693391322109068261351915526432114955808528229911617056416714805914686353797976102953069696414088314800561761039350070201261640008021040989637202012616400080176103935007014088314800561029530696964686353797976416714805914229911617056114955808528519155264322109068261376693391322481256778708930508177232627383205687059052108600813575113244946441
第45行:
14599014190148995122175981450604537962021555319588616313531901872861015059591028760021745730062090451668713349603448674255846466264229701103068603890171588449494024383621770203169870830126377365575015041167153638004116715363800377365575015031698708301262438362177020171588449494011030686038906466264229703448674255841668713349607300620904528760021745101505959103190187286886163135215553195453796208145060122175914899514190990451
第46行:
146103515180163185137075493668195352468026093281511017163304076350421133407831963891061765510176623079023987754400551173876054499149384855417496950268602818953098830415424667196056082330071466943526580276789037111395082334307276007890371113950694352658027656082330071464154246671960281895309883017496950268609914938485545117387605442398775440051017662307903891061765513340783196407635042111017163302609328155352468093668191370754163185151801035461
第47行:
14710811621517836515339391073757362891499314457495136264914551780667511741713361752251400851140676848445341643774795751616304549150323260909827411888754144568648125690697319977079097624796791061255175958742214833897694226161238018415501612380184155014833897694226125517595874229762479679106697319977079045686481256902741188875414150323260909875161630454934164377479514067684844552251400851174171336175178066751136264914531445749562891499107375731533939178365162151081471
第48行:
14811281729619458017123041227151273629072377348994167710664065407158962259520036869668534468192928249296482320623240109326007934422548489136474244421484512730983700110411541847896480167356794498962231423926652827385657281648309576995357763224760368310030957699535776273856572816482231423926652816735679449896115418478964807309837001104424442148451222548489136471093260079344482320623240192928249296696685344682259520036865407158961677106640377348994
73629072122715121712304194580172961128481
第49行:
14911761842421187619068841398381685900584450978066205445563482178225362913591626492263734836262596783764675248872536157558070258433481089929916499270398159115542584856161885168489758428277527346376390499187164244969989654817658343356817424632053032188766320530321887658343356817424496998965481763904991871642428277527346376188516848975841155425848561664992703981593348108992991157558070258467524887253626259678376492263734836291359162648217822536205445563445097806685900584139838161906884211876184241176491
歷史發展
北宋人賈憲約1050年首先使用“賈憲三角”進行高次開方運算。
13世紀中國宋代數學家楊輝在《詳解九章算術》里討論這種形式的數表,並說明此表引自11世紀前半賈憲的《釋鎖算術》,並繪畫了“古法七乘方圖”。故此,楊輝三角又被稱為“賈憲三角”。
元朝數學家朱世傑在《四元玉鑒》(1303年)擴充了“賈憲三角”成“古法七乘方圖”。
義大利人稱之為“塔塔利亞三角形”(TriangolodiTartaglia)以紀念在16世紀發現一元三次方程解的塔塔利亞。
在歐洲直到1623年以後,法國數學家帕斯卡在13歲時發現了“帕斯卡三角”。
布萊士·帕斯卡的著作Traitédutrianglearithmétique(1655年)介紹了這個三角形。帕斯卡蒐集了幾個關於它的結果,並以此解決一些機率論上的問題,影響面廣泛,PierreRaymonddeMontmort(1708年)和亞伯拉罕·棣·美弗(1730年)都用帕斯卡來稱呼這個三角形。
近年來國外也逐漸承認這項成果屬於中國,所以有些書上稱這是“中國三角形”(Chinesetriangle)
歷史上曾經獨立繪製過這種圖表的數學家
·賈憲中國北宋11世紀《釋鎖算術》
·楊輝中國南宋1261《詳解九章算法》記載之功
·朱世傑中國元代1299《四元玉鑒》級數求和公式
·阿爾·卡西阿拉伯1427《算術的鑰匙》
·阿皮亞納斯德國1527
·米歇爾`斯蒂費爾德國1544《綜合算術》二項式展開式係數
·薛貝爾法國1545
·B·帕斯卡法國1654《論算術三角形》
其實,中國古代數學家在數學的許多重要領域中處於遙遙領先的地位。中國古代數學史曾經有自己光輝燦爛的篇章,而楊輝三角的發現就是十分精彩的一頁。
賈憲
中國北宋11世紀《釋鎖算術》
賈憲最著名的數學成就,是他創製了一幅數字圖式,即“開方作法本源圖”(見下圖)。這幅圖現見於楊輝的書中,但楊輝在引用了這幅圖後特意說明:“賈憲用此術”。所以過去我國數學界把這幅圖稱為“楊輝三角”,實際上是不妥當的,應該稱為“賈憲三角”才最為恰當。由於史書沒有賈憲的傳記,幸虧南宋數學家楊輝在他的書中引述了賈憲的許多數學思想資料,才使我們今天得以了解賈憲在數學上的重大貢獻。
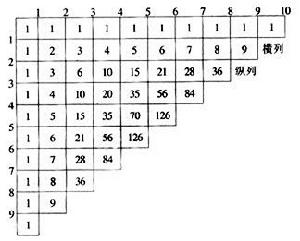 圖形
圖形·楊輝中國南宋1261《詳解九章算法》記載之功
·朱世傑中國元代1299《四元玉鑒》級數求和公式
·阿爾·卡西阿拉伯1427《算術的鑰匙》
·阿皮亞納斯德國1527
·施蒂費爾德國1544《綜合算術》二項式展開式係數
·薛貝爾法國1545
·B·帕斯卡法國1654《論算術三角形》
楊輝三角的三個基本性質主要是二項展開式的二項式係數即組合數的性質,它是研究楊輝三角其他規律的基礎。楊輝三角橫行的數字規律主要包括橫行各數之間的大小關係。組合關係以及不同橫行數字之間的聯繫。
C#輸出
classProgram
{
publicvoidyanghui(intvalue)
{
if(value<3)
{
Console.WriteLine("請重新輸入數組大於3的值!");
}
else
{
int[,]arry=newint[value,value];
Console.WriteLine("數組為:");
for(inti=0;i<value;i++)
{
stringstr="";
str=str.PadLeft(value-i);
Console.Write(str);
for(intj=0;j<=i;j++)
{
if(i==j||j==0)
{
arry[i,j]=1;
}
else
{
arry[i,j]=arry[i-1,j-1]+arry[i-1,j];
}
Console.Write(arry[i,j]+"");
}
Console.WriteLine();
}
}
}
staticvoidMain(string[]args)
{
Programp=newProgram();
Console.WriteLine("請輸入數組值:");
stringstr_name=Console.ReadLine();
intvalue=Convert.ToInt16(str_name);
p.yanghui(value);
Console.Readkey();
}
}
C語言輸出楊輝三角
classProgram
{
publicvoidyanghui(intvalue)
{
if(value<3)
{
Console.WriteLine("請重新輸入數組大於3的值!");
}
else
{
int[,]arry=newint[value,value];
Console.WriteLine("數組為:");
for(inti=0;i<value;i++)
{
stringstr="";
str=str.PadLeft(value-i);
Console.Write(str);
for(intj=0;j<=i;j++)
{
if(i==j||j==0)
{
arry[i,j]=1;
}
else
{
arry[i,j]=arry[i-1,j-1]+arry[i-1,j];
}
Console.Write(arry[i,j]+"");
}
Console.WriteLine();
}
}
}
staticvoidMain(string[]args)
{
Programp=newProgram();
Console.WriteLine("請輸入數組值:");
stringstr_name=Console.ReadLine();
intvalue=Convert.ToInt16(str_name);
p.yanghui(value);
Console.Readkey();
}
}
 金字塔楊三角
金字塔楊三角#include<stdio.h>intmain(){
inta[10][10],i,j;
for(i=0;i<10;i++){
for(j=10;j>=i;j--)
printf("%2c",'');/*兩個空格*/
for(j=0;j<=i;j++){
if(i==j||j==0)
a[i][j]=1;
else
a[i][j]=a[i-1][j]+a[i-1][j-1];
printf("%3d",a[i][j]);/*%3d後一個空格*/
if(i==j)
printf("\n");
}
}
return0;
}
二維數組輸出前十行
1
2
#include<stdio.h>intmain(){inta[10][10],i,j;for(i=0;i<10;i++){a[i][i]=1;a[i][0]=1;}for(i=2;i<10;i++)for(j=1;j<=i-1;j++)a[i][j]=a[i-1][j-1]+a[i-1][j];for(i=0;i<10;i++){for(j=0;j<=i;j++)printf("%6d",a[i][j]);printf("\n");}printf("\n");return0;}菱形楊三角
#include<stdio.h>intmain(void){inti,j;inta[6][6];//該程式輸出為6層,可根據需要更改數組大小printf("\n\n\n");for(i=0;i<6;i++)for(j=0;j<=i;j++){if(j==0||j==i)a[i][j]=1;elsea[i][j]=a[i-1][j-1]+a[i-1][j];}for(i=0;i<6;i++){for(j=0;j<=6-i;j++)printf("%2c",'');for(j=0;j<=i;j++)printf("%4d",a[i][j]);printf("\n");}for(i=4;i>=0;i--){for(j=0;j<=6-i;j++)printf("%2c",'');for(j=0;j<=i;j++)printf("%4d",a[i][j]);printf("\n");}return0;}
運行結果
佇列輸出
1
2
#include<stdio.h>#include<stdlib.h>#defineERROR0#defineOK1#defineOVERFLOW-1#defineMAX_QUEUE100typedefintDataType;typedefstruct{DataTypeelem[MAX_QUEUE];intfront;intrear;}LinkQueue;intInitQueue(LinkQueue*);voidEnQueue(LinkQueue*,DataType);voidDeQueue(LinkQueue*,DataType*);voidGetFront(LinkQueue,DataType*);intQueueEmpty(LinkQueue);voidYangHuiTriangle(int);intmain(void){intn=1;printf("pleaseenteranumber:");scanf("%d",&n);if(n<=0){printf("ERROR!\n");exit(0);}YangHuiTriangle(n);return0;}intInitQueue(LinkQueue*Q){Q->front=Q->rear=-1;return1;}voidEnQueue(LinkQueue*Q,DataTypee){if((Q->rear+1)%MAX_QUEUE==Q->front)exit(OVERFLOW);else{Q->rear=(Q->rear+1)%MAX_QUEUE;Q->elem[Q->rear]=e;}}voidDeQueue(LinkQueue*Q,DataType*e){if(QueueEmpty(*Q)){printf("queueisempty\n");exit(0);}else{Q->front=(Q->front+1)%MAX_QUEUE;*e=Q->elem[Q->front];}}voidGetFront(LinkQueueQ,DataType*e){if(QueueEmpty(Q)){printf("queueisempty\n");exit(0);}else*e=Q.elem[(Q.front+1)%MAX_QUEUE];}intQueueEmpty(LinkQueueQ){if(Q.front==Q.rear)return1;elsereturn0;}voidYangHuiTriangle(intn){LinkQueueQ;inti,j,k,t,s,e;InitQueue(&Q);for(i=0;i<n;i++)printf("");printf("1\n");EnQueue(&Q,1);EnQueue(&Q,1);for(i=1;i<n;i++){for(k=0;k<n-i;k++)printf("");EnQueue(&Q,1);for(j=0;j<i;j++){DeQueue(&Q,&t);printf("%3d",t);GetFront(Q,&s);e=t+s;EnQueue(&Q,e);}EnQueue(&Q,1);DeQueue(&Q,&t);printf("%d\n",t);}}VB輸出
PrivateSubForm_click()n=Val(Text1.Text)ReDima(n+1,n+1),b(n+1,n+1)Clsk=8Fori=1TonPrintString((n-i)*k/2+1,"");Forj=1Toia(i,1)=1a(i,i)=1a(i+1,j+1)=a(i,j)+a(i,j+1)b(i,j)=Trim(Str(a(i,j)))Printb(i,j);String(k-Len(b(i,j)),"");NextjPrintNextiEndSub
創建一個text和command,在text中輸入所需行數,點擊command即可。一個數在楊輝三角出現的次數 由1開始,正整數在楊輝三角形出現的次數為∞:1,2,2,2,3,2,2,2,4,2,2,2,2,4,...(OEIS:A003016)。最小而又大於1的數在賈憲三角形至少出現n次的數為2,3,6,10,120,120,3003,3003,...(OEIS:A062527)
除了1之外,所有正整數都出現有限次。
只有2出現剛好一次。
6,20,70等出現三次。
出現兩次和四次的數很多。
還未能找到出現剛好五次的數。
120,210,1540等出現剛好六次。(OEIS:A098565)
因為丟番圖方程:
有無窮個解,所以出現至少六次的數有無窮個多。
其解答,是
,
。
其中Fn表示第n個斐波那契數(F1=F2=1)。
3003是第一個出現八次的數。
一道NOIP楊輝三角題目:
#include<stdio.h>#definemaxn50constinty=2009;intmain(){intn,c[maxn][maxn],i,j,s=0;scanf("%d",&n);c[0][0]=1;for(i=1;i<=n;i++){c[i][0]=1;for(j=1;j<i;j++)c[i][j]=c[i-1][j-1]+c[i-1][j];c[i][i]=1;}for(i=0;i<=n;i++)s=(s+c[n][i])%y;printf("%d\n",s);return0;}
此為利用數組求和
JAVA輸出楊輝三角
代碼:
importjava.util.Scanner;
publicclassTriangleYH{
publicstaticvoidmain(String[]args){
Scannersuin=newScanner(System.in);
System.out.println("請輸入一個大於3的數:");
intn=suin.nextInt()+1;//這裡如果不+1,那么輸出的結果少了一行,+1則全部輸出。
intyh[][]=newint[n][n];
if(n<3)System.out.println("輸入錯誤");
for(inti=1;i<n;i++){
yh[i][0]=1;//始終輸出第一行和最後一行的1.
for(intj=1;j<i;j++){
yh[i][j]=yh[i-1][j-1]+yh[i-1][j];//計算其它行的數字,並存入數組。
}
}
for(intk=0;k<n;k++){
for(intt=0;t<k;t++){
System.out.print(yh[k][t]+"");
}
System.out.println();
}
}
}
結果:
SQL輸出
--返回某一數的階乘值createfunctionJi(@countint)returnsintasbegindeclare@uint,@indexintset@u=1--初使值為1set@index=1while(@index<=@count)beginset@u=@u*@indexset@index=@index+1endreturn(@u)endcreatefunctionVa(@numint,@countint)returnsintasbegindeclare@upint,@L1int,@R1int,@Iintset@up=dbo.Ji(@count)set@L1=dbo.Ji(@num)set@R1=dbo.Ji(@count-@num)set@I=@up/(@L1*@R1)return(@I)endcreatefunctionPrintRow(@numint)returnsnvarchar(100)asbegindeclare@iintdeclare@strnvarchar(100)set@str="";set@i=1while(@i<@num)beginset@str=@str+replace(str(dbo.Va(@i,@num)),'','')+','set@i=@i+1endreturn(@str)endcreateprocPrintJiCeng(@numint)asbegindeclare@iintset@i=1while(@i<=@num)beginif(@i=0)print1+','elseif(@i=1)print'1,1,'elseprint'1,'+dbo.PrintRow(@i)+'1,'set@i=@i+1endend--計算10以內的揚輝三角execPrintJiCeng10PHP輸出<?php$row=20;//所要輸出的行號for($i=0;$i<$row;$i++){for($j=0;$j<=$i;$j++){if($j==0||$i==$j){print$a[$i][$j]=1;}else{print$a[$i][$j]=$a[$i-1][$j-1]+$a[$i-1][$j];}print'&bnsp;&bnsp;';}print"<br/>";}?>C++輸出直角三角形//單數組動態規劃輸出楊輝三角,以下截止第31行#include<iostream>usingnamespacestd;#defineMAXH31intmain(){inti,j;unsignedlongnum[MAXH]={0};num[0]=1;for(i=0;i<MAXH;i++){for(j=i;j>0;j--){num[j]=num[j]+num[j-1];//A[i,j]=A[i,j-1]+A[i,j]cout<<num[j]<<"";}cout<<"1"<<endl;}return0;}直角三角形#include<iostream>usingnamespacestd;intmain(){inth,i,j;cout<<"請輸入楊輝三角的高度:"<<endl;cin>>h;inta[10][10];for(i=0;i<10;i++){a[i][i]=1;a[i][0]=1;}for(i=2;i<10;i++)for(j=1;j<=i-1;j++)a[i][j]=a[i-1][j-1]+a[i-1][j];for(i=0;i<=h;i++){for(j=0;j<=i;j++)cout<<a[i][j]<<'\t';cout<<endl;}return0;}等腰三角形#include<iostream>usingnamespacestd;intmain(){inti,j,h,a[10][10];cout<<"請輸入楊輝三角的高度:"<<endl;cin>>h;for(i=0;i<=h;i++){for(j=0;j<=i;j++){if(i==j||j==0)a[i][j]=1;elsea[i][j]=a[i-1][j]+a[i-1][j-1];}}for(i=0;i<=h;i++){for(j=h;j>=i;j--)cout<<"";for(j=0;j<=i;j++){cout<<a[i][j]<<'\t';if(i==j)cout<<endl;}}return0;}直角三角形#include<iostream>usingnamespacestd;intcomputeTriangleElement(intlevel,intindex){if(index==1||index==level)return1;returncomputeTriangleElement(level-1,index-1)+computeTriangleElement(level-1,index);}voidyanghuiTriangle(intlevel){for(inti=1;i<=level;i++){for(intj=1;j<=i;j++){cout<<computeTriangleElement(i,j)<<'';}cout<<endl;}}intmain(){intlevel;cout<<"請輸入楊輝三角的高度:"<<endl;cin>>level;yanghuiTriangle(level);return0;}易語言輸出
來自易語言自帶的例子。
以下為全文。
.版本2
.程式集啟動視窗程式集
.程式集變數帕斯卡三角階數,整數型,,,帕斯卡三角行數
.程式集變數帕斯卡三角,文本型,,,形成的帕斯卡三角
.子程式__啟動視窗_創建完畢
'使用算法:遞歸調用
'問題:求帕斯卡(楊輝)三角
'問題描述:取N階的帕斯卡(楊輝)三角並顯示
'問題分析:
' 運用遞歸的方法取N層帕斯卡三角,並顯示。三角形邊界上的數都是1,內部的每個數是位於它上面的兩個數之和。
' 三角形邊界上的數都是1,內部的每個數是位於它上面的兩個數之和。假設f(row,col)表示楊輝三角的第row行的第col個元素,那么:f(row,col)=1(col=1或者row=col),也就是遞歸的停止條件。f(row,col)=f(row-1,col-1)+f(row-1,col),也就是上一行的兩個相鄰元素的和。遞歸調用求解。
'備註:
.子程式_計算圖形按鈕_被單擊
.局部變數行數,整數型,,,帕斯卡三角行數
.局部變數列數,整數型,,,帕斯卡三角列數
.局部變數詢問返回,整數型,,,信息框返回的結果
編輯框2.內容=“”
帕斯卡三角=“”
'判斷輸入的值
.判斷開始(編輯框1.內容=“”)
信息框(“輸入錯誤!”,0,)
'當數值過大時,給出提示
.判斷(到數值(編輯框1.內容)>20)
詢問返回=信息框(“您輸入的數值過大,處理數據時程式將會有一段時間無回響,是否繼續?”,#是否鈕+#詢問圖示,“請問:”)
.如果真(詢問返回=#是鈕)
'如果確定,調用求帕斯卡三角
求帕斯卡三角()
.如果真結束
'數據較小時調用求帕斯卡三角
.判斷(編輯框1.內容≠“”且到數值(編輯框1.內容)≤20)
求帕斯卡三角()
.默認
.判斷結束
.子程式求帕斯卡三角
.局部變數行數,整數型,,,帕斯卡三角行數
.局部變數列數,整數型,,,帕斯卡三角列數
'要求的帕斯卡三角的總行數
帕斯卡三角階數=到數值(編輯框1.內容)-1
.變數循環首(0,帕斯卡三角階數,1,行數)
.變數循環首(0,行數,1,列數)
'取帕斯卡三角元素放到當前行里
帕斯卡三角=帕斯卡三角+到文本(取帕斯卡三角元素(行數+1,列數+1))+“,”
.變數循環尾()
帕斯卡三角=取文本左邊(帕斯卡三角,取文本長度(帕斯卡三角)-1)+#換行符
'沒層需去尾都好加換行符
.變數循環尾()
'顯示結果
編輯框2.內容=帕斯卡三角
.子程式取帕斯卡三角元素,整數型,,取帕斯卡三角中元素的子程式
.參數行數,整數型,,帕斯卡三角行數
.參數列數,整數型,,帕斯卡三角列數
.如果(列數=1或行數=列數)
'每行的外圍兩個元素為1
返回(1)
.否則
'其餘的部分為上一行的(行數-1)和(行數)元素之和
返回(取帕斯卡三角元素(行數-1,列數-1)+取帕斯卡三角元素(行數-1,列數))
.如果結束
PHP輸出
<?phpheader("Content-Type:text/html;charset=UTF-8");
functionyhsj($ln)
{
$int=1;
if($ln<3)
{
die('請輸入大於2的值!');
}
$arr=array();
$arr[1][1]=$int;
$ints=str_pad(" ",($ln-1)*12," ");
echo$ints.$int."<br/>";
for($i=2;$i<=$ln;$i++)
{
for($j=1;$j<=$i;$j++)
{
if($j==1)
{
echostr_pad(" ",($ln-$i)*12," ");
}
echo$arr[$i][$j]=$arr[$i-1][$j]+$arr[$i-1][$j-1];
echo" ";
}
echo"<br/>";
}
}
yhsj(3);
?>
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |