| 排列 |
定義
從n個不同元素中,任取m(m≤n)個元素按照一定的順序排成一列,叫做從n個不同元素中取出m個元素的一個排列;
從n個不同元素中取出m(m≤n)個元素的所有排列的個數,叫做從n個不同元素中取出m個元素的排列數,
用符號p(n,m)表示.p(n,m)=n(n-1)(n-2)……(n-m+1)=n!/(n-m)!(規定0!=1).
基本原理
兩個基本計數原理及套用
(1)加法原理和分類計數法
1.加法原理
2.加法原理的集合形式
3.分類的要求:每一類中的每一種方法都可以獨立地完成此任務;兩類不同辦法中的具體方法,互不相同(即分類不重);完成此任務的任何一種方法,都屬於某一類(即分類不漏)
(2)乘法原理和分步計數法
1.乘法原理
2.合理分步的要求內容
根據定義,兩個排列相同,當且僅當,兩個排列的元素完全相同,且元素排列順序也完全相同。
從n個不同元素中取m(m<=n)個元素的所有排列個數,叫做從n個不同元素中取出m元素的排列數,
計算公式:
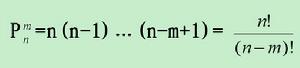 排列
排列P,即Permutation,有時也用A(Array)表示。
例題
[例題分析]排列組合思維方法選講
1.首先明確任務的意義
例1.
從1、2、3、……、20這二十個數中任取三個不同的數組成等差數列,這樣的不同等差數列有________個。
分析:首先要把複雜的生活背景或其它數學背景轉化為一個明確的排列組合問題。
設a,b,c成等差,
∴2b=a+c,可知b由a,c決定,
又∵2b是偶數,
∴a,c同奇或同偶,即:從1,3,5,……,19或2,4,6,8,……,20這十個數中選出兩個數進行排列,由此就可確定等差數列,
因而本題為C(2,1)*C(10,2)*C(2,1)=2*45*2=180。
例2.
某城市有4條東西街道和6條南北的街道,街道之間的間距相同,如圖。若規定只能向東或向北兩個方向沿圖中路線前進,則從M到N有多少種不同的走法?
分析:對實際背景的分析可以逐層深入
(一)從M到N必須向上走三步,向右走五步,共走八步。
(二)每一步是向上還是向右,決定了不同的走法。
(三)事實上,當把向上的步驟決定後,剩下的步驟只能向右。
從而,任務可敘述為:從八個步驟中選出哪三步是向上走,就可以確定走法數,
∴本題答案為:C(8,3)=56。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |

