名稱介紹
函式的單調性也叫函式的增減性.函式的單調性是對某個區間而言的,它是一個局部概念.
 函式圖
函式圖基本方法
先要弄清概念和研究目的,因為函式本身是動態的,所以判斷函式的單調性、奇偶性,還有研究函式切線的斜率、極值等等,都是為了更好地了解函式本身所採用的方法。其次就解題技巧而言,當然是立足於掌握課本上的例題,然後再找些典型例題做做就可以了,這部分知識僅就應付解題而言應該不是很難。最後找些考試試卷題目來解,針對考試會出的題型強化一下.
1.把握好函式單調性的定義。證明函式單調性一般(初學最好用定義)用定義(謹防循環論證),如果函式解析式異常複雜或者具有某種特殊形式,可以採用函式單調性定義的等價形式證明。另外還請注意函式單調性的定義是[充要命題]。
2.熟練掌握基本初等函式的單調性及其單調區間。理解並掌握判斷複合函式單調性的方法:同增異減。
3.高三選修課本有導數及其套用,用導數求函式的單調區間一般是非常簡便的。還應注意函式單調性的套用,例如求極值、比較大小,還有和不等式有關的問題。
一般的,求函式單調性有如下幾個步驟:
1、取值X1,X2屬於{?},並使X1<X2<
2、作差f(x1)-f(x2)
3、變形
4、定號(判斷f(x1)-f(x2)的正負)
5、下結論
判斷複合函式的單調性
1.導數
2.構造基本初等函式(已知單調性的函式)
3.複合函式根據同增異減口訣,先判斷內層函式的單調性,再判斷外層函式單調性,在同一定義域上,若兩函式單調性相同,則此複合函式在此定義域上為增函式,反之則為減函式。
4.定義法
5.數形結合
複合函式的單調性一般是看函式包含的兩個函式的單調性(1)如果兩個都是增的,那么函式就是增函式(2)一個是減一個是增,那就是減函式(3)兩個都是減,那就是增函式
複合函式求導公式
F'(g(x))=[F(g(x+dx))-F(g(x))]/dx......(1)g(x+dx)-g(x)=g'(x)*dx=dg(x)........(2)g(x+dx)=g(x)+dg(x).........(3)F'(g(x))=[F(g(x)+dg(x))-F(g(x))]/dx=[F(g(x)+dg(x))-F(g(x))]/dg(x)*dg(x)/dx=F'(g)*g'(x)
特徵
一般地,設函式f(x)的定義域為I:
如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2,當x1<x2時都有f(x1)<f(x2)。那么就說f(x)在這個區間上是增函式。 相反地,如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2,當x1<x2時都有f(x1)>f(x2).那么就是f(x)在這個區間上是減函式。
基本性質
⒈ 增函式與減函式
一般地,設函式f(x)的定義域為I:
如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2,當x1、x2時都有f(x1)< f(x2).那么就說f(x)在 這個區間上是增函式。
如果對於屬於I內某個區間上的任意兩個自變數的值x1、x2,當x1<x2時都有f(x1)>f(x2).那么就是f(x)在這個區間上是減函式。
⒉ 單調性與單調區間
若函式y=f(x)在某個區間是增函式或減函式,則就說函式在這一區間具有(嚴格的)單調性,這一區間叫做函式的單調區間.此時也說函式是這一區間上的單調函式.
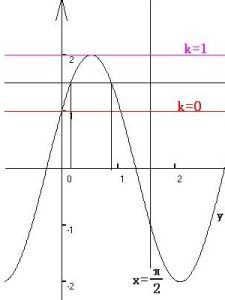
在單調區間上,增函式的圖像是上升的,減函式的圖像是下降的。
規律
若函式y=f(x)在某個區間是增函式或減函式,則就說函式在這一區間具有(嚴格的)單調性,這一區間叫做函式的單調區間。此時也說函式是這一區間上的單調函式。在單調區間上,增函式的圖像是上升的,減函式的圖像是下降的。
註:在單調性中有如下性質。
圖例:↑(增函式)↓(減函式)
↑+↑=↑ 兩個增函式之和仍為增函式
↑-↓=↑ 增函式減去減函式為增函式
↓+↓=↓ 兩個減函式之和仍為減函式
↓-↑=↓ 減函式減去增函式為減函式
複合函式
在函式y=f[g(x)]的定義域內,令u=g(x),則y=f[g(x)]的單調性由u=g(x)與y=f(u)的單調性共同確定,方法如下u=g(x)y=f(u)y=f[g(x)]
增函式增函式 增函式
減函式 減函式 增函式
增函式減函式減函式
減函式增函式減函式
因此,複合函式的單調性可用“同增異減”來判定,但要考慮某些特殊函式的定義域。
註:y=f(x)+g(x)不屬於複合函式,因此不在此方法的適用範圍內。
例題解析
判斷函式的單調性y=1/(x^2-2x-3)。設x^2-2x-3=t,令x^2-2x-3=0,
解得:x=3或x=-1,
當x>3和x<-1時,t>0,
當-1<x<3時,t<0。
所以得到x^2-2x-1對稱軸是1。
根據反比例函式性質:
在整個定義域上是1/t是減函式。
當t>0時,x>3時,
t是增函式,1/t是減函式,
所以(3,+∞)是減區間,
而x<-1時,t是減函式,
所以1/t是增函式。
因此(-∞,-1)是增區間,
當x<0時,-1<x<1,t是減函式,
所以1/t是增函式,因此(-1,1)是增區間,
而1<x<3時,t是增函式,1/t是減函式,
因此(1,3)是減區間,
得到增區間是(-∞,-1)和(-1,1),(1,3)和(3,+∞)是減區間。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |