歷史
大約在公元前480年，古巴比倫人和中國人已經使用配方法求得了二次方程的正根，但是並沒有提出通用的求解方法。公元前300年左右，歐幾里得提出了一種更抽象的幾何方法求解二次方程。
7世紀印度的婆羅摩笈多是第一位懂得用使用代數方程的人，它同時容許有正負數的根。
11世紀阿拉伯的花拉子密 獨立地發展了一套公式以求方程的正數解。亞伯拉罕·巴希亞（亦以拉丁文名字薩瓦索達著稱）在他的著作Liber embadorum中，首次將完整的一元二次方程解法傳入歐洲。
據說施里德哈勒是最早給出二次方程的普適解法的數學家之一。但這一點在他的時代存在著爭議。這個求解規則是（引自婆什迦羅第二）
基本定義
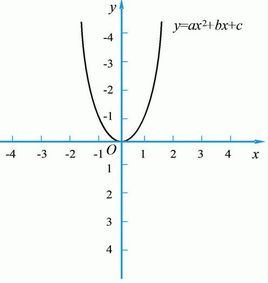
二次函式一般地，把形如y=ax^2+bx+c（其中a，b，c是常數，a≠0，bc可以為0）的函式叫做二次函式（quadratic function），其中a稱為二次項係數，b為一次項係數，c為常數項。x為自變數，y為因變數。等號右邊自變數的最高次數是2。二次函式圖像是軸對稱圖形。對稱軸為直線x=-b/2a。頂點坐標[-b/2a,(4ac-b^2)/4a]交點式為y=a(X-x1)(X-x2) [僅限於與x軸有交點A（x1，0）和 B（x2，0）的拋物線]
注意：“變數”不同於“自變數”，不能說“二次函式是指自變數的最高次數為二次的多項式函式”。“未知數”只是一個數（具體值未知，但是只取一個值），“變數”可在實數範圍內任意取值。在方程中適用“未知數”的概念（函式方程、微分方程中是未知函式，但不論是未知數還是未知函式，一般都表示一個數或函式——也會遇到特殊情況），但是函式中的字母表示的是變數，意義已經有所不同。從函式的定義也可看出二者的差別.如同函式不等於函式的關係。
函式性質
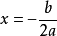二次函式1.二次函式是拋物線，但拋物線不一定是二次函式。開口向上或者向下的拋物線才是二次函式。拋物線是軸對稱圖形。對稱軸為直線。
對稱軸與拋物線唯一的交點為拋物線的頂點P。特別地，當b=0時，拋物線的對稱軸是y軸（即直線x=0）。
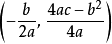二次函式2.拋物線有一個頂點P，坐標為P。當時，P在y軸上；當時，P在x軸上。
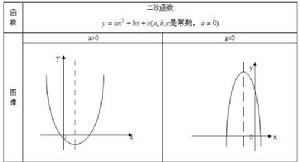
3.二次項係數a決定拋物線的開口方向和大小。當a>0時，拋物線開口向上；當a<0時，拋物線開口向下。|a|越大，則拋物線的開口越小。|a|越小，則拋物線的開口越大。
4.一次項係數b和二次項係數a共同決定對稱軸的位置。當a與b同號時（即ab>0），對稱軸在y軸左；當a與b異號時（即ab<0），對稱軸在y軸右。（可巧記為：左同右異）
5.常數項c決定拋物線與y軸交點。拋物線與y軸交於(0, c）
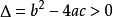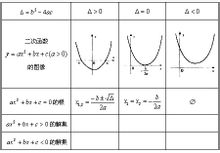
二次函式6.拋物線與x軸交點個數：
時，拋物線與x軸有2個交點。
時，拋物線與x軸有1個交點。當
時，拋物線與x軸沒有交點。
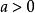二次函式當
時，函式在
處取得最小值
；在
上是減函式，在
上是增函式；拋物線的開口向上；函式的值域是。
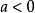二次函式當時，函式在處取得最大值；在上是增函式，在上是減函式；拋物線的開口向下；函式的值域是。
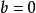二次函式當時，拋物線的對稱軸是y軸，這時，函式是偶函式，解析式變形為y=ax²+c(a≠0)。
7.定義域：R
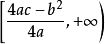二次函式值域：當a>0時，值域是；當a<0時，值域是。
奇偶性：當b=0時，此函式是偶函式；當b不等於0時，此函式是非奇非偶函式。
周期性：無
解析式：
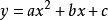二次函式①一般式：
⑴a≠0
⑵若a>0，則拋物線開口朝上；若a<0，則拋物線開口朝下；
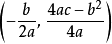二次函式⑶頂點：
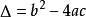二次函式⑷若Δ>0，則函式圖像與x軸交於兩點：
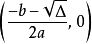二次函式若Δ=0，則函式圖像與x軸切於一點：
若Δ<0，函式圖像與x軸無公共點；
②頂點式：
此時頂點為（h,t)時，對應頂點為
③交點式：
函式圖像與x軸交於和兩點。
表達式
頂點式
y=a(x-h)²+k(a≠0,a、h、k為常數),頂點坐標為（h,k)，對稱軸為直線x=h，頂點的位置特徵和圖像的開口方向與函式y=ax²的圖像相同，當x=h時，y最大（小）值=k.有時題目會指出讓你用配方法把一般式化成頂點式。
例：已知二次函式y的頂點(1,2)和另一任意點(3,10)，求y的解析式。
解：設y=a(x-1)²+2，把(3,10)代入上式，解得y=2(x-1)²+2。
注意：與點在平面直角坐標系中的平移不同，二次函式平移後的頂點式中，h>0時，h越大，圖像的對稱軸離y軸越遠，且在x軸正方向上，不能因h前是負號就簡單地認為是向左平移。
具體可分為下面幾種情況：
當h>0時，y=a(x-h)²的圖像可由拋物線y=ax²向右平行移動h個單位得到；
當h<0時，y=a(x-h)²的圖像可由拋物線y=ax²向左平行移動|h|個單位得到；
當h>0,k>0時，將拋物線y=ax²向右平行移動h個單位，再向上移動k個單位，就可以得到y=a(x-h)²+k的圖象；
當h>0,k<0時，將拋物線y=ax²向右平行移動h個單位，再向下移動|k|個單位可得到y=a(x-h)²+k的圖象；
當h<0,k>0時，將拋物線y=ax²向左平行移動|h|個單位，再向上移動k個單位可得到y=a(x-h)²+k的圖象；
當h<0,k<0時，將拋物線y=ax²向左平行移動|h|個單位，再向下移動|k|個單位可得到y=a(x-h)²+k的圖象。
交點式
[僅限於與x軸即y=0有交點時的拋物線，即b2-4ac≥0].
已知拋物線與x軸即y=0有交點A(x1,0)和B(x2,0),我們可設,然後把第三點代入x、y中便可求出a。
由一般式變為交點式的步驟：(韋達定理)
重要概念：a，b，c為常數，a≠0，且a決定函式的開口方向。a>0時，開口方向向上；a<0時，開口方向向下。a的絕對值可以決定開口大小。a的絕對值越大開口就越小，a的絕對值越小開口就越大。
f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0)...(x-xn-1)+Rn(x)由此可引導出交點式的係數(y為截距) 二次函式表達式的右邊通常為二次三項式。
歐拉交點式：
若ax²+bx+c=0有兩個實根x1,x2，則此拋物線的對稱軸為直線。
三點式
方法1：
已知二次函式上三個點，(x1,y1)、(x2,y2)、(x3,y3)。把三個點分別代入函式解析式y=a(x-h)²+k(a≠0,a、h、k為常數)，有：
得出一個三元一次方程組，就能解出a、b、c的值。
方法2：
已知二次函式上三個點，(x1,y1)、(x2,y2)、(x3,y3)
利用拉格朗日插值法，可以求出該二次函式的解析式為：
與X軸交點的情況:
當時，函式圖像與x軸有兩個交點，分別是(x1,0)和(x2,0)。
當時，函式圖像與x軸只有一個切點，即。
當時，拋物線與x軸沒有公共交點。x的取值範圍是虛數（）
函式圖像
基本圖像
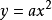二次函式在平面直角坐標系中作出二次函式y=ax+bx+c的圖像，可以看出，在沒有特定定義域的二次函式圖像是一條永無止境的拋物線。 如果所畫圖形準確無誤，那么二次函式圖像將是由
平移得到的。
軸對稱
二次函式圖像二次函式圖像是軸對稱圖形。對稱軸為直線
對稱軸與二次函式圖像唯一的交點為二次函式圖象的頂點P。
特別地，當b=0時，二次函式圖像的對稱軸是y軸（即直線x=0）。是頂點的橫坐標（即x=？）。
a,b同號，對稱軸在y軸左側；
a,b異號，對稱軸在y軸右側。
頂點
二次函式圖像有一個頂點P，坐標為P(h,k)。
當h=0時，P在y軸上；當k=0時，P在x軸上。即可表示為頂點式y=a(x-h)+k（x≠0）
開口
二次項係數a決定二次函式圖像的開口方向和大小。
當a>0時，二次函式圖象向上開口；當a<0時，拋物線向下開口。
|a|越大，則二次函式圖像的開口越小。
決定位置因素
一次項係數b和二次項係數a共同決定對稱軸的位置。
當a>0,與b同號時（即ab>0），對稱軸在y軸左； 因為對稱軸在左邊則對稱軸小於0，也就是- b/2a<0,所以 b/2a要大於0，所以a、b要同號
當a>0,與b異號時（即ab<0），對稱軸在y軸右。因為對稱軸在右邊則對稱軸要大於0，也就是- b/2a>0, 所以b/2a要小於0，所以a、b要異號
可簡單記憶為左同右異，即當對稱軸在y軸左時，a與b同號（即a>0，b>0或a<0，b<0）；當對稱軸在y軸右時，a與b異號（即a0或a>0，b<0）（ab<0）。
事實上，b有其自身的幾何意義：二次函式圖象與y軸的交點處的該二次函式圖像切線的函式解析式（一次函式）的斜率k的值。可通過對二次函式求導得到。
決定交點因素
常數項c決定二次函式圖像與y軸交點。
二次函式圖像與y軸交於（0,C）點
注意：頂點坐標為（h,k)， 與y軸交於（0,C)。
與x軸交點數
a<0;k>0或a>0;k<0時，二次函式圖像與x軸有2個交點。
k=0時，二次函式圖像與x軸只有1個交點。
質疑點：a<0;k<0或a>0,k>0時，二次函式圖像與x軸無交點。
當a>0時，函式在x=h處取得最小值
=k，在xh範圍內是增函式（即y隨x的變大而變大），二次函式圖像的開口向上，函式的值域是y>k
當a<0時，函式在x=h處取得最大值
=k，在xh範圍內是減函式（即y隨x的變大而變小），二次函式圖像的開口向下，函式的值域是y
當h=0時，拋物線的對稱軸是y軸，這時，函式是偶函式
五點法
五點草圖法又被叫做五點作圖法是二次函式中一種常用的作圖方法。
註明：雖說是草圖，但畫出來絕不是草圖。
五點草圖法中的五個點都是極其重要的五個點，分別為：頂點，與x軸交點與y軸交點及其對稱點。
Ps.僅是草圖，正規考試會扣分
描點法
在國中數學中，要求採用描點法畫出二次函式圖像。
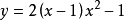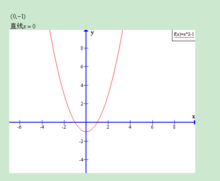
二次函式其做法與五點法類似：【以
為例】
1、列表
| x | …… | -1 | -0.5 | 0 | 1 | 2 | 2.5 | 3 | …… |
 | …… | 7 | 3.5 | 1 | -1 | 1 | 3.5 | 7 | …… |
y=2先取頂點，用虛線畫出對稱軸。取與x軸兩個交點（如果存在）、y
軸交點及其對稱點（如果存在）和另外兩點及其對稱點。
Ps.原則上相鄰x的差值相等，但遠離頂點的點可以適當減小差值
2、依據表格數據繪製函式圖像,如圖
學習方法
知識要點
1.要理解函式的意義。
2.要記住函式的幾個表達形式，注意區分。
3.一般式，頂點式，交點式，等，區分對稱軸，頂點，圖像，y隨著x的增大而減小（增大）(增減值）等的差異性。
4.聯繫實際對函式圖象的理解。
5.計算時，看圖像時切記取值範圍。
6.隨圖象理解數字的變化而變化。 二次函式考點及例題
二次函式知識很容易與其他知識綜合套用，而形成較為複雜的綜合題目。因此，以二次函式知識為主的綜合性題目是中考的熱點考題，往往以大題形式出現。
誤區提醒
（1）對二次函式概念理解有誤，漏掉二次項係數不為0這一限制條件；
（2）對二次函式圖像和性質存在思維誤區；
（3）忽略二次函式自變數取值範圍；
（4）平移拋物線時，弄反方向
定義與表達式
一般地，自變數x和因變數y之間存在如下關係：
y=ax²+bx+c
（a，b，c為常數，a≠0，且a決定函式的開口方向，a>0時，開口方向向上，a<0時，開口方向向下，IaI還可以決定開口大小，IaI越大開口就越小，IaI越小開口就越大.）
則稱y為x的二次函式。
二次函式表達式的右邊通常為二次三項式。
三種表達式
一般式：y=ax²+bx+c（a，b，c為常數，a≠0）
頂點式：y=a(x-h)²+k[拋物線的頂點P(h, k)]
交點式：y=a(x-x)(x-x)[僅限於與x軸有交點A（x，0）和B（x，0）的拋物線]
註：在3種形式的互相轉化中，有如下關係：
拋物線的性質
1.拋物線是軸對稱圖形。對稱軸為直線。
對稱軸與拋物線唯一的交點為拋物線的頂點P。
特別地，當b=0時，拋物線的對稱軸是y軸（即直線x=0）
2.拋物線有一個頂點P，坐標為
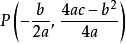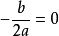二次函式
二次函式當時，P在y軸上；當時，P在x軸上。
3.二次項係數a決定拋物線的開口方向，|a|決定拋物線開口大小。
當a>0時，拋物線開口向上；當a<0時，拋物線開口向下
|a|越大，則拋物線的開口越小。
4.一次項係數b和二次項係數a有1個交點。
5.常數項c決定拋物線與y軸交點。
拋物線與y軸交於（0，c）
拋物線與x軸
交點個數
Δ=b²-4ac>0時，拋物線與x軸有2個交點。
Δ=b²-4ac=0時，拋物線與x軸有1個交點。
Δ=b²-4ac<0時，拋物線與x軸沒有交點。
常用工具
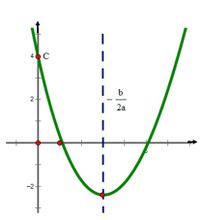幾何畫板畫出的拋物線圖象幾何畫板軟體——基礎代數幾何必備。
注意：左加右減，上加下減
盤點高中數學名詞
| 高中是大學的過渡階段，學好高中數學，才能為學好大學數學打好基礎，那我們盤點下高中數學中有哪些名詞吧。 |
