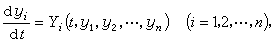正文
它是研究擾動性因素對運動系統的影響。這種擾動性因素,可以是瞬間的作用,引起系統的初始狀態的變化;也可以是持續地起作用,而引起系統本身的變化。通常著重考慮的是前者。微小的擾動對於不同的系統運動的影響是不一樣的。對有些運動,影響不顯著,受擾動的運動與未受擾動的運動相差很小。而對有些運動,擾動的影響可能很顯著,以致無論擾動如何小,受擾動的運動與未受擾動的運動隨時間的推移可能相差很大。簡略地說,屬於前者的運動是穩定的,屬於後一類型的運動是不穩定的。運動穩定性理論就是要建立一些準則,用來判斷所考慮的運動是穩定的或不穩定的。一般,動力系統的數學模型可寫成
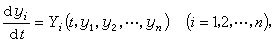 (1)
(1)
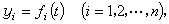
如果對於任意正數 ε,無論它多么小,總可以找到另一個正數 η(ε),使得對於所有受擾動的運動 yi=yi(t)(i=1,2,…,n),只要在初始時刻t=t0滿足不等式
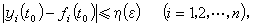 (2)
(2)
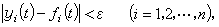 (3)
(3)
為了研究方程(1)的特解yi=ƒi(t)(i=1,2,…,n)的穩定性問題,一般比較困難。為此,對方程(1)引進坐標變換
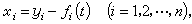 (4)
(4)
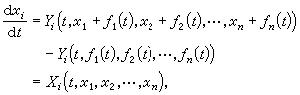 (5)
(5)
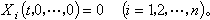
此時,不等式(2)及(3)分別變成
 (6)
(6)
 (7)
(7)
如果對於任意正數ε,無論它多么小, 都可以選取另一個正數 η(ε), 使得對於所有受干擾的運動xi=xi(t)(i=1,2,…,n),只要在初始時刻t0時滿足不等式(6),就在所有t≥t0時滿足不等式(7),則稱(5)的未受擾動的運動xi=0(i=1,2,…,n)是穩定的。否則,則稱 xi=0(i=1,2,…,n)是不穩定的。
如果未受擾動的運動xi=0(i=1,2,…,n)是穩定的,並且數 η可選得如此之小,使得對於所有滿足不等式(6)的受干擾運動,都滿足條件
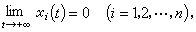
這就是李亞普諾夫在他的博士論文《運動穩定性一般問題》(1892)中所給出的有關常微分方程解的穩定性定義,通常稱為李亞普諾夫意義下的穩定性。它有下列幾個特點:①首先,李亞普諾夫穩定性概念是一個局部概念,它涉及到在被考慮的狀態附近的特性,因此初始擾動的範圍較小,即η值較小;②時間t取值在無限長區間【t0,+
 )上;③初始擾動的大小與初始時刻t0的選取無關;④在初始擾動後無其他外界干擾;⑤未受擾動的運動與受擾動的運動服從於同一個方程,而且對二者在同一時刻進行比較。
)上;③初始擾動的大小與初始時刻t0的選取無關;④在初始擾動後無其他外界干擾;⑤未受擾動的運動與受擾動的運動服從於同一個方程,而且對二者在同一時刻進行比較。 由於在一般情況下所研究的微分方程,它的解都不能求出來,因此李亞普諾夫在他的上述論文中,提出了兩種解決問題的方法,稱之為李亞普諾夫第一方法和第二方法。
李亞普諾夫第一方法 基於研究微分方程組的通解或特解而研究受擾動運動的所有方法,都歸屬為第一方法。這個方法一般需要去尋求按任意常數的正整數冪的無窮級數或具有另一些特徵的級數形式的解,故又稱冪級數展開法。考慮微分方程組
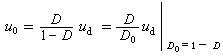 (8)
(8)
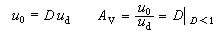
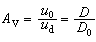
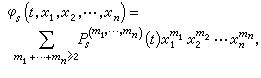 (9)
(9)
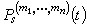 對一切t∈【t0,+
對一切t∈【t0,+ )連續、有界,且滿足
)連續、有界,且滿足 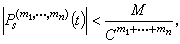 (10)
(10)
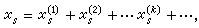 (11)
(11)
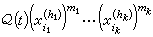 為項的新的冪級數,其中Q(t)表示t的函式。用R扤表示這個新的冪級數中m1h1+…+mkhk=m的一切項的有限和。再令
為項的新的冪級數,其中Q(t)表示t的函式。用R扤表示這個新的冪級數中m1h1+…+mkhk=m的一切項的有限和。再令 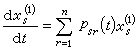
 (12)
(12)
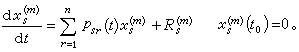 (13)
(13)
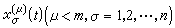 和(9)的係數psr(t)及
和(9)的係數psr(t)及 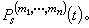 因此,由(12)、(13)可逐項地確定x扏,x扐,…,從而形式地得到級數(11)。李亞普諾夫證明:給定任意有限區間【t0,T】(T>t0),存在常數A,0<A<C,使得對於一切初值α=(α1,α2,…,αn),‖α‖≤A,級數(11)對一切t∈【t0,T】和‖α‖≤A絕對且一致收斂,且xs(t)是(8)的滿足xs(t0)=αs(s=1,2,…,n)的惟一解。進一步,在另一些附加條件下,他還證明了:對一切t≥t0,所得的(11)仍是(8)的解,即證得在區間【t0,+
因此,由(12)、(13)可逐項地確定x扏,x扐,…,從而形式地得到級數(11)。李亞普諾夫證明:給定任意有限區間【t0,T】(T>t0),存在常數A,0<A<C,使得對於一切初值α=(α1,α2,…,αn),‖α‖≤A,級數(11)對一切t∈【t0,T】和‖α‖≤A絕對且一致收斂,且xs(t)是(8)的滿足xs(t0)=αs(s=1,2,…,n)的惟一解。進一步,在另一些附加條件下,他還證明了:對一切t≥t0,所得的(11)仍是(8)的解,即證得在區間【t0,+ )上解的存在性,從而得出關於解的穩定性的結論(見下面定理)。這表明李亞普諾夫存在定理,原則上不同於柯西-皮卡存在定理,它不僅在穩定性方面,而且在常微分方程理論中有非常重要的作用。
)上解的存在性,從而得出關於解的穩定性的結論(見下面定理)。這表明李亞普諾夫存在定理,原則上不同於柯西-皮卡存在定理,它不僅在穩定性方面,而且在常微分方程理論中有非常重要的作用。 李亞普諾夫在他研究的第一方法中,引入下述重要概念。
① 特征數 設ƒ(t)是定義在t∈【t0,+
 )上的連續函式,若存在實數λ,對任何實數ε>0,有
)上的連續函式,若存在實數λ,對任何實數ε>0,有 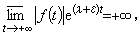
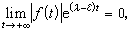
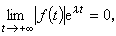 定義ⅹ{ƒ}=+
定義ⅹ{ƒ}=+ ;如果對一切實數λ都有
;如果對一切實數λ都有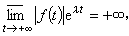 定義 ⅹ{ƒ}=-
定義 ⅹ{ƒ}=- ,函式ƒ(t)的特徵數 ⅹ{ƒ} 可用公式
,函式ƒ(t)的特徵數 ⅹ{ƒ} 可用公式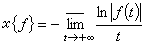 計算。函式組x(t)=(x1(t),x2(t),…,xn(t))的特徵數記成ⅹ{x1(t),ⅹ2(t),…,xn(t)}或ⅹ{x(t)},它定義為ⅹ{x(t)}=min{ⅹ{x1(t)},ⅹ{x2(t)},…,ⅹ{xn(t)}}。
計算。函式組x(t)=(x1(t),x2(t),…,xn(t))的特徵數記成ⅹ{x1(t),ⅹ2(t),…,xn(t)}或ⅹ{x(t)},它定義為ⅹ{x(t)}=min{ⅹ{x1(t)},ⅹ{x2(t)},…,ⅹ{xn(t)}}。 李亞普諾夫建立了具有連續、有界係數的線性微分方程組
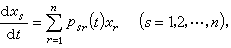 (14)
(14)

③ 正則系統 (14)稱為正則系統,如果(14)的正規解系使得 s+μ=0,其中
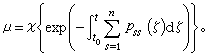 (14)稱為非正則系統,如果它的正規解系使得s+μ<0。
(14)稱為非正則系統,如果它的正規解系使得s+μ<0。 李亞普諾夫第一方法關於穩定性的定理是:設方程組 (8)滿足條件 (9)、(10),其中係數psr(t)、
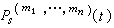 是t在【t0,+
是t在【t0,+ 】上的連續、有界函式;又設(8)的一次近似系統(14)是正則系統,它的所有特徵數都是正的。則(8)的零解 x1=x2=…=xn=0是漸近穩定的。定理中加之於φs(t,x1,x2,…,xn)的條件可以減弱。例如,只需假設φs在域│xs│≤H(s=1,2,…,n),t≥t0中滿足條件
】上的連續、有界函式;又設(8)的一次近似系統(14)是正則系統,它的所有特徵數都是正的。則(8)的零解 x1=x2=…=xn=0是漸近穩定的。定理中加之於φs(t,x1,x2,…,xn)的條件可以減弱。例如,只需假設φs在域│xs│≤H(s=1,2,…,n),t≥t0中滿足條件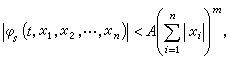 其中A>0,m>1為常數,並保證(8)的初值問題的解的存在、惟一性。
其中A>0,m>1為常數,並保證(8)的初值問題的解的存在、惟一性。 常係數線性系統和周期係數線性系統都是正則系統。常係數線性系統的特徵數是該系統的特徵根的實部反號。周期係數線性系統的特徵數是該系統的特徵指數的實部反號。由此可相應地得出當(8)的一次近似系統 (14)為常係數系統或周期係數系統時,關於(8)的零解為漸近穩定的定理(見線性常微分方程)。
李亞普諾夫同時還證明,如果 (8)的一次近似系統(14)不是正則系統,即s+μ=-σ<0,而(14) 的所有特徵數λk>σ ,其他條件仍如定理所述, 則(8)的零解是漸近穩定的。
李亞普諾夫第一方法依賴於一次近似系統的特徵數的研究。特徵數在變係數線性方程組中的地位,猶如特徵根在常係數線性方程組中的地位那樣重要。這些數表征出當t→+
 時解的增長程度,故它在研究解的漸近性態時,有其根本意義。但是決定變係數線性方程組解的特徵數是很困難的。線性方程組的微小變化是否也只引起特徵數的微小變化?И.Γ.馬爾金於1952年提出線性方程組的特徵數穩定的概念,並建立了判定線性方程組的特徵數穩定的若干準則。Б.Ф.貝洛夫等人,不僅對擾動是線性項的系統,而且對擾動是非線性項的系統的最大(小)特徵數的上(下)穩定問題和特徵數的重合問題,作了深入的研究。至今,特徵數理論已經向多方面發展。
時解的增長程度,故它在研究解的漸近性態時,有其根本意義。但是決定變係數線性方程組解的特徵數是很困難的。線性方程組的微小變化是否也只引起特徵數的微小變化?И.Γ.馬爾金於1952年提出線性方程組的特徵數穩定的概念,並建立了判定線性方程組的特徵數穩定的若干準則。Б.Ф.貝洛夫等人,不僅對擾動是線性項的系統,而且對擾動是非線性項的系統的最大(小)特徵數的上(下)穩定問題和特徵數的重合問題,作了深入的研究。至今,特徵數理論已經向多方面發展。 以一次近似判定非線性系統的穩定性問題,除上述李亞普諾夫工作外,Ο.佩隆、К.∏.佩爾西德斯基、馬爾金和R.貝爾曼等人都做過大量的研究。值得指出的是,佩隆舉例說明,對於滿足上述條件的任意φs,僅由一次近似方程組(14)的零解漸近穩定性,還不足以保證非線性方程組(8)的零解的穩定性。
李亞普諾夫直接法 即李亞普諾夫第二方法,它不需要尋求運動方程的特殊解。把未受擾動的運動的穩定性歸結為平衡位置(即(5)的平凡解xi=0(i=1,2,…,n)的穩定性問題後,李亞普諾夫將穩定或者不穩定的事實與某些具有特殊性質的函式 V(x1,x2,…,xn)的存在性聯繫起來。這個函式沿著軌線對時間 t的全導數具有某些確定的性質。例如,方程
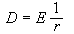 (15)
(15)
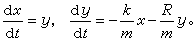 (16)
(16)
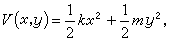 (17)
(17)
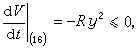 故知(16)的平凡解是穩定的。又如對方程組
故知(16)的平凡解是穩定的。又如對方程組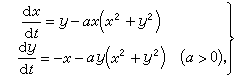 (18)
(18)
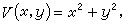 (19)
(19)
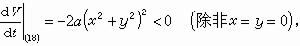 (20)
(20)
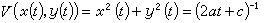 (c是任意正常數)。
(c是任意正常數)。
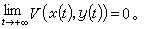 即
即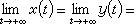
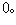 故知(18)的平凡解是漸近穩定的。(20)說明了封閉曲線族x2+y2=C沿著(18)的相軌線按t的增加方向不斷地收縮,直至收縮到原點。換句話說,(18)的相軌線隨著t的增加由外向里地穿過每一條閉曲線V(x,y)=C,最終趨於原點。這裡,函式(19)表示了在相平面上由(18)所描述的運動質點與原點之間的距離平方。因此
故知(18)的平凡解是漸近穩定的。(20)說明了封閉曲線族x2+y2=C沿著(18)的相軌線按t的增加方向不斷地收縮,直至收縮到原點。換句話說,(18)的相軌線隨著t的增加由外向里地穿過每一條閉曲線V(x,y)=C,最終趨於原點。這裡,函式(19)表示了在相平面上由(18)所描述的運動質點與原點之間的距離平方。因此 (當x2+y2≠0)就表示了這個距離隨著時間的增長在不斷地減小,並最終趨於零。前面的函式(17)亦具有與(19)同樣的性質。
(當x2+y2≠0)就表示了這個距離隨著時間的增長在不斷地減小,並最終趨於零。前面的函式(17)亦具有與(19)同樣的性質。 從上述兩例可以看出:研究由常微分方程組來描述的動力系統的穩定性時,可以不必去求它的特解與通解,而是構造一類具有特殊性質的函式V(x,y),由這個函式來控制相軌線的動向,來解決未被擾動運動的穩定性問題。稱這種類型的函式V 為李亞普諾夫函式。它有各種構造方法,一般要結合實際的物理背景來作。
通常總假定函式V在坐標原點鄰域內連續單值,V(0,0,…,0)=0,且有連續的偏導數。稱函式V(x1,x2,…,xn)為定號的(正定的或負定的),如果當│xs│≤h(h是足夠小的正數,s=1,2,…,n)時,它只能取具有固定符號的值,且只在xs=0(s=1,2,…,n)時,取零值。稱V(x1,x2, …, xn) 為常號的(正的或負的),如果它在區域|xs|≤h(s=1,2,…,n)內只能取具有一定符號的值,但它可以在
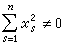 時取零值。稱 V(x1,x2,…,xn)為變號的,如果它既不是定號的,也不是常號的,亦即,無論數h多么小,它在區域內既可取到正值,也可取到負值。通常取二次型作為李亞普諾夫函式,這是用得最廣泛的一種。
時取零值。稱 V(x1,x2,…,xn)為變號的,如果它既不是定號的,也不是常號的,亦即,無論數h多么小,它在區域內既可取到正值,也可取到負值。通常取二次型作為李亞普諾夫函式,這是用得最廣泛的一種。 下面介紹李亞普諾夫關於穩定性的幾個定理。
考慮自治系統(或稱駐定系統,即方程右邊與t無關的系統)
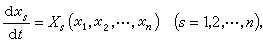 (21)
(21)
定理 1 如果可以找到一個定號函式 V (x1,x2,…,xn),它關於時間t的由(21)構成的全導數
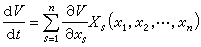
定理2 如果可以找到定號函式 V(x1,x2,…,xn),它對於時間t由(21)構成的全導數也是定號的,但是其正負號與V的正負號相反,則(21)的未被擾動運動xs=0(s=1,2,…,n)是漸近穩定的。
定理3 如果可以找到函式V(x1,x2,…,xn),它對於時間t由(21)構成的全導數是定號函式,而函式V本身卻不是與
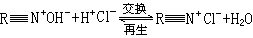 的符號相反的常號函式,則(21)的未被擾動運動xs=0 (s=1,2,…,n)是不穩定的。
的符號相反的常號函式,則(21)的未被擾動運動xs=0 (s=1,2,…,n)是不穩定的。 定理4 如果存在函式V(x1,x2,…,xn),它對於時間t由(21)構成的全導數為
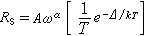 其中λ>0是常數,而 W(x1,x2,…,xn)或者恆等於零,或者是常號函式,並且在後一種情形,V不是與 W 的符號相反的常號函式,則(21)的未被擾動運動xs=0(s=1,2,…,n)是不穩定的。
其中λ>0是常數,而 W(x1,x2,…,xn)或者恆等於零,或者是常號函式,並且在後一種情形,V不是與 W 的符號相反的常號函式,則(21)的未被擾動運動xs=0(s=1,2,…,n)是不穩定的。 在定理3中,要求導數
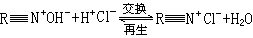 是定號的這個條件可以削弱,如果代之以
是定號的這個條件可以削弱,如果代之以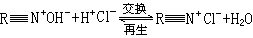 在V>0的區域內的所有點上都取正值,則定理的結論仍然是正確的。首先指出這一點的是H.Γ.切塔耶夫。他得到如下定理:如果對於(21)可以找到如此的函式V(x1,x2,…,xn),使得:①在坐標原點任意小的鄰域存在V>0的區域,在它的邊界上V=0;②在區域V>0的所有點上,
在V>0的區域內的所有點上都取正值,則定理的結論仍然是正確的。首先指出這一點的是H.Γ.切塔耶夫。他得到如下定理:如果對於(21)可以找到如此的函式V(x1,x2,…,xn),使得:①在坐標原點任意小的鄰域存在V>0的區域,在它的邊界上V=0;②在區域V>0的所有點上, 取正值。則(21)的未被擾動運動是xs=0 (s=1,2,…,n)不穩定的。
取正值。則(21)的未被擾動運動是xs=0 (s=1,2,…,n)不穩定的。 E.A.巴爾巴申和H.H.克拉索夫斯基給出了關於漸近穩定性定理的改進,其特點是藉助於有常號導數的李亞普諾夫函式來解決漸近穩定性問題,且將其推廣到全空間,得到如下的定理:如果對於方程組(21)存在正定函式V(x1,x2,…,xn),使得
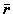
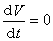 的集合中除原點外不包含整條正半軌線,那么(21)的未被擾動運動xs=0(s=1,2,…,n)是漸近穩定的。
的集合中除原點外不包含整條正半軌線,那么(21)的未被擾動運動xs=0(s=1,2,…,n)是漸近穩定的。 對於非駐定系統,李亞普諾夫類似地建立了判斷未被擾動運動穩定、漸近穩定和不穩定的定理。
運用上面的定理,李亞普諾夫還研究了一次近似為常係數的非線性系統的零解的穩定性問題。特別是對於特徵方程中有一個零根或兩個零根或一對共軛純虛根、而其他根都具有負實部這三種臨界情形都作了仔細分析;對於一次近似是周期係數的情形,他分析了特徵方程中有一個根等於1和有兩個共軛虛根具有模等於1的情形。
前面已指出:李亞普諾夫意義下的穩定性質是局部性的概念,但處理局部問題的李亞普諾夫函式的思想方法,完全可推廣到全相空間。事實上,在50年代初,人們對自動調節系統的研究中所遇到的盧里耶問題以及奧澤爾曼問題就出現過初始擾動任意大的情形,從而很自然地要去研究未被擾動運動的全局漸近穩定性問題。此時(21)的右端函數是在全空間Rη上滿足保證解的存在惟一性條件。不妨設xs=0(s=1,2,…,n)是(21)的惟一奇點。如果(21)的零解是穩定的,並且對於(21)的所有解,都有
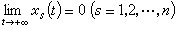 則稱(21)的零解是全局漸近穩定的。
則稱(21)的零解是全局漸近穩定的。 巴爾巴申和克拉索夫斯基引進無限大函式的概念,即:如果函式V(x1,x2,…,xn)對任何大的數K>0,都存在數R>0,使得只要
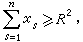 就有|V(x1,x2,…,xn)|>K,則稱函式 V具有無限大性。他們很自然地把李亞普諾夫的局部漸近穩定性定理推廣到全空間,得到下述定理:①如果存在定號無限大函式V(x1,x2,…,xn),它關於t的由方程組(21)構成的全導數
就有|V(x1,x2,…,xn)|>K,則稱函式 V具有無限大性。他們很自然地把李亞普諾夫的局部漸近穩定性定理推廣到全空間,得到下述定理:①如果存在定號無限大函式V(x1,x2,…,xn),它關於t的由方程組(21)構成的全導數 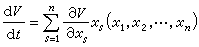
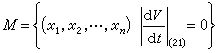
J.P.拉薩爾更聯繫解的ω極限集(見拓撲動力系統)建立了不變性原理:設 G為Rn中列緊集,從 G出發的方程組(21)的軌線, 在未來時刻仍保留在集G 中;如果在G 記憶體在函式 V(x1,x2,…,xn),使
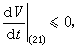 記
記
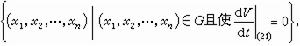 又M是E中的最大不變集,則由G內出發的(21)的每一條軌線當t→+
又M是E中的最大不變集,則由G內出發的(21)的每一條軌線當t→+ 時必趨向於M。顯然,如果G=Rn,M={(0,0,…,0},且(21)的一切解均有界,則(21)的零解是全局漸近穩定的。
時必趨向於M。顯然,如果G=Rn,M={(0,0,…,0},且(21)的一切解均有界,則(21)的零解是全局漸近穩定的。 自動調節系統的穩定性在現代工業中的作用是眾所周知的。調節系統分直接調節系統和間接調節系統兩大類。它們的數學模型分別是
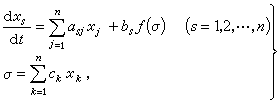 (22)
(22)
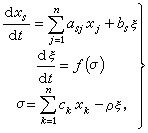 (23)
(23)
 (24)
(24)
 )內是絕對穩定的。判定絕對穩定的主要途徑是選取正定無限大函式,給出條件保證其全導數是負定的。
)內是絕對穩定的。判定絕對穩定的主要途徑是選取正定無限大函式,給出條件保證其全導數是負定的。 除了上述一些類型的穩定性外,還有如李亞普諾夫研究過的有關部分變元的穩定性。馬爾金研究過的經常擾動下的穩定性。拉薩爾、S.萊夫謝茨指出的實際穩定性,以及目前蓬勃發展的大系統穩定性,還有與動力系統有密切聯繫的軌道穩定與結構穩定性等等。
隨著科學技術的迅速發展,李亞普諾夫創立的運動穩定性理論,不僅在力學、控制、工程及星際航行等科學尖端技術領域有其廣泛深刻的套用,而且在現代物理、生物、化學等自然科學中得到了進一步的發展,同時它亦逐漸發展成為常微分方程學科本身許多課題理論研究的有力工具。李亞普諾夫穩定性理論中的一個核心問題,就是李亞普諾夫函式的構造問題。30多年來人們作了不少的努力,但對於一般非線性系統,還沒有得到通用而有效的構造方法。雖然如此,針對實際問題中出現的各種非線性系統,通過定性分析並根據實際情況進行具體分析,從而構造出恰當的李亞普諾夫函式,還是取得了豐富的成果。