概念
 極限
極限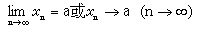
歷史
極限思想在古希臘的窮竭法和中國古代的割圓術中已經萌芽。在牛頓的微積分中也含有極限思想。但是,直到19世紀初,人們對極限的理解還沒有擺脫幾何直觀。只是到了1821年,法國數學家A.L.柯西才把極限概念建立在算術的基礎上。他把極限定義為:若變數的一串數值無限地趨向某一定值時,其差可以隨意地小,則該定值稱為這一串數值的極限。19世紀70年代,德國的K.魏爾施特拉斯等人在數學分析的算術化過程中,進一步用"ε-N"語言更精確地把極限概念表述為:如果序列x1,x2,...xn,...對於任意給定的無論怎樣小的正數ε,總存在一個正整數N,使得當n>N時,不等式ㄧxn-aㄧ<ε恆成立,則稱數a為該序列的極限。
極限概念體現了有限與無限的對立統一關係。序列x1,x2,...xn,...是由無限多個有限值組成的,並且在收斂的條件下,存在著有限的極限值。這說明了無限包含著有限,並且在一定條件下,可以向有限轉化;另一方面,有限又包含著無限,在一定條件下,可以轉化為無限,並通過無限表現自身。這一點在函式f(x)的級數展開式
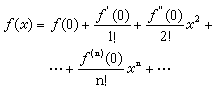
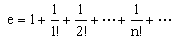
求得。這表明極限概念具有重要的方法論意義。
數列極限
 極限
極限數列的定義
一個定義在正整數集合上的函式yn=f(n)(稱為整標函式),當自變數n按正整數1,2,3…依次增大的順序取值時,函式值按相應的順序排成一串數:f(1),f(2),f(3),…,f(n),…稱為一個無窮數列,簡稱數列。數列中的每一個數稱為數列的項,f(n)稱為數列的一般項。
數列的極限
如果對於任意給定的正數c,總存在一個正整數N,當n>N時,∣yn-A∣
此定義中的正數c只有任意給定,不等式
才能表達出xn與a無限接近的意思。且定義中的正整數N與任意給定的正數c是有關的,它是隨著c的給定而選定的。函式極限
函式的極值有兩種情況:a):自變數無限增大;b):自變數無限接近某一定點x0,如果在這時,函式值無限接近於某一常數A,就叫做函式存在極值。
a):自變數趨向無窮大時函式的極限
設函式y=f(x),若對於任意給定的正數ε(不論其多么小),總存在著正數X,使得對於適合不等式
的一切x,所對應的函式值f(x)都滿足不等式那么常數A就叫做函式y=f(x)當x→∞時的極限,記作:b):自變數趨向有限值時函式的極限
設函式f(x)在某點x0的某個去心鄰域內有定義,且存在數A,如果對任意給定的ε(不論其多么小),總存在正數δ,當0<
變數極限
 極限
極限如果對於任意給定的正數C在變數Y變化過程中,總有那么一個時刻,在那個時刻以後,
恆成立,則稱變數y變化過程中以常數A極限,記作。如果在某一變化過程中,變數Y有極限,則變數Y是(局部)有界變數。
無窮大量
已知函式,當x→0時,可知,我們把這種情況稱為趨向無窮大。為此我們可定義如下:
設有函式y=,在x=x0的去心鄰域內有定義,對於任意給定的正數N(一個任意大的數),總可找到正數δ,當時,成立,則稱函式當時為無窮大量。記為:(表示為無窮大量,實際它是沒有極限的)。
無窮小量
以零為極限的變數稱為無窮小量。
定義:設有函式
對於任意給定的正數C不論它多么小),總存在正數N(或正數M),使得對於適合不等式或的一切x,所對應的函式值滿足不等式,則稱函式當(或x→∞)時為無窮小量。記作:或。無窮大量與無窮小量都是一個變化不定的量,不是常量,只有0可作為無窮小量的唯一常量。
無窮大量與無窮小量的區別是:前者無界,後者有界,前者發散,後者收斂於0。
無窮大量與無窮小量是互為倒數關係的。
極限思想
極限的思想是近代數學的一種重要思想,數學分析就是以極限概念為基礎、極限理論(包括級數)為主要工具來研究函式的一門學科。所謂極限的思想,是指用極限概念分析問題和解決問題的一種數學思想。
用極限思想解決問題的一般步驟可概括為:對於被考察的未知量,先設法構思一個與它有關的變數,確認這變數通過無限過程的結果就是所求的未知量;最後用極限計算來得到這結果。極限思想是微積分的基本思想,數學分析中的一系列重要概念,如函式的連續性、導數以及定積分等等都是藉助於極限來定義的。如果要問:“數學分析是一門什麼學科?”那么可以概括地說:“數學分析就是用極限思想來研究函式的一門學科”。
經濟套用數學
| 經濟套用數學是高等學校財經類專業的必學內容。此任務主要對微積分的基本知識進行概述講解。提供給剛入門此專業的學生。希望對他們有所幫助。 |

