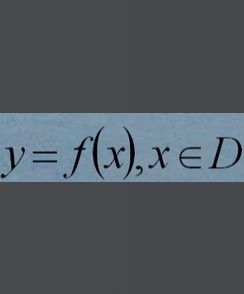定義
設A,B是兩個非空數集,從集合A到集合B的一個映射,叫做從集合A到集合B的一個函式。記作y=f(x),x∈A.或y=g(t),t∈A其中A就叫做定義域。通常,用字母D表示。通常定義域是F(X)中x的取值範圍。
1,給定定義域:例如:函式y=2x-1,x∈{1,2}的定義域為給定的集合{1,2}。
2,一般函式的定義域:使函式有意義的一切實數。例如:函式y=1/x的定義域為{x∈R∣x≠0}。R為任意實數。也可以寫做x∈(—∞,0)∪(0,+∞)
3,實際問題:根據具體情況求定義域。
求法
抽象函式定義域的常見題型有三種:1,已知f(x)的定義域,求f(g(x))的定義域.
例1,已知f(x)的定義域為(-1,1),求f(2x-1)的定義域.
略解:由-1<2x-1<1有0<x<1
∴f(2x-1)的定義域為(0,1)
2,已知f(g(x))的定義域,求f(x)的定義域.
例2,已知f(2x-1)的定義域為(0,1),求f(x)的定義域。
解:已知0<x<1,設t=2x-1
∴x=(t+1)/2
∴0<(t+1)/2<1
∴-1<t<1
∴f(x)的定義域為(-1,1)
注意比較例1與例2,加深理解定義域為x的取值範圍的含義。
3,已知f(g(x))的定義域,求f(h(x))的定義域.
例3,已知f(2x-1)的定義域為(0,1),求f(x-1)的定義域。
略解:如例2,先求出f(x)的定義域為(-1,1),然後如例1
有-1<x-1<1,即0<x<2
∴f(x-1)的定義域為(0,2)
指使函式有意義的一切實數所組成的集合。
其主要根據:
①分式的分母不能為零
②偶次方根的被開方數不小於零
③對數函式的真數必須大於零
④指數函式和對數函式的底數必須大於零且不等於1
⑤對數函式的真數必須大於零
例4,已知f(x)=1/x+√(x+1),求f(x)的定義域。
略解:x≠0且x+1≧0,
∴f(x)的定義域為[-1,0)∪(0,+∞)
注意:答案一般用區間表示。
例5,已知f(x)=lg(-x2+x+2),求f(x)的定義域。
略解:由-x2+x+2>0有x2-x-2<0
即-1<x<2
∴f(x)的定義域為(-1,2)
函式套用題的函式的定義域要根據實際情況求解。
例6,某工廠統計資料顯示,產品次品率p與日產量x(件)(x∈N,1≦x<99)的關係符合如下規律:
x1234…89p2/991/492/971/48…2/11
又知每生產一件正品盈利100元,每生產一件次品損失100元.
求該廠日盈利額T(元)關於日產量x(件)的函式;
解:由題意:當日產量為x件時,次品率p=2/(100-x)
則次品個數為:2x/(100-x),正品個數為:x-2x/(100-x)所以T=100[x-2x/(100-x)]-100·2x/(100-x)
即T=100[x-4x/(100-x)],(x∈N且1≦x≦89)
數學名詞
A-F▪八邊形▪八面體▪百分比▪百分點▪百分位數▪半徑▪半球▪半圓
▪被乘數▪被除數▪被加數▪被減數
▪比▪比例▪邊▪變數
▪標準差▪表面積▪並集▪補集
▪不等邊三角形▪不等式▪不定積分▪差
▪長▪常量▪乘▪乘方
▪乘數▪除▪除數▪垂心
▪次方▪次方根▪大於▪大於等於
▪代數▪單調性▪單項式▪導數
▪等邊三角形▪等式方程式▪等腰三角形▪等腰梯形
▪等於▪底▪底面▪點
▪定積分▪定理▪定義域▪對數
▪鈍角▪鈍角三角形▪多邊形▪多面體
▪二次方程▪多項式▪二次方根平方根▪二次方平方
▪二進制▪二十面體▪反餘割▪反餘切
▪反餘弦▪反正割▪反正切▪反正弦
▪方差▪非常態分配▪分布▪分母
▪分數▪分子▪負▪複數
G-L▪高▪公理▪公式▪勾股定理
▪軌跡▪函式▪和▪橫坐標
▪弧▪弧度▪環▪積
▪積分▪極限▪集合▪幾何
▪計算▪加▪加權平均數▪加數
▪假設▪減▪減數▪交集
▪角▪角度▪階乘▪截尾
▪進位▪九邊形▪九面體▪矩形
▪矩陣▪開方▪空集▪空間
▪寬▪稜台▪稜柱▪稜錐
▪立方體▪菱形▪零▪六邊形
▪六面體
M-R▪面▪面積▪命題▪內切圓
▪內心▪排列▪旁心▪拋物線
▪平角▪平均數▪平行▪平行六面體
▪平行四邊形▪七邊形▪七面體▪奇偶性
▪球▪曲線統計圖▪全等▪權
▪銳角▪銳角三角形
S-Z▪三次方程▪三次方根立方根▪三次方立方▪三角
▪三角形▪扇形▪扇形統計圖▪商
▪上捨入▪射線▪十邊形▪十二邊形
▪十二面體▪十進制▪十六進制▪十面體
▪十一邊形▪十一面體▪實數▪數
▪數列級數▪數字▪雙曲線▪四邊形
▪四次方▪四次方程▪四次方根▪四面體
▪四捨五入▪算術▪梯形▪體
▪體積▪條形統計圖▪統計▪圖表
▪圖象▪橢圓▪外切圓▪外心
▪微分▪微積分▪未知數▪無理數
▪無窮大▪無窮小▪無效數字▪五邊形
▪五面體▪係數▪下捨入▪線
▪線段▪相交▪相似▪相位
▪小數▪小數點▪小於▪小於等於
▪斜邊▪行列式▪虛數▪鏇轉
▪一次方程▪映射▪有理數▪有效數字
▪餘割▪餘切▪餘弦▪元素
▪原點▪圓▪圓台▪圓心
▪圓周▪圓周率▪圓柱▪圓錐
▪運算▪運算符▪折線統計圖▪振幅
▪整數▪正▪正多邊形▪正方形
▪正割▪正切▪常態分配▪正弦
▪證明▪直角▪直角邊▪直角三角形
▪直角梯形▪直徑▪值域▪指數冪
▪重心▪周長▪周角▪周期
▪周期性▪軸▪柱形統計圖▪子集
▪自然數▪縱坐標▪組合▪坐標系
▪坐標軸
相關簡介
還有值域。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |