簡介
所謂反函式(inversefunction)就是將原函式中自變數與變數調換位置,用原函式的變數表示自變數而形成的函式。一般地,設函式y=f(x)(x∈A)的值域是C,根據這個函式中x,y的關係,用y把x表示出,得到x=g(y).若對於y在C中的任何一個值,通過x=g(y),x在A中都有唯一的值和它對應,那么,x=g(y)就表示y是自變數,x是因變數y的函式,這樣的函式x=g(y)(y∈C)叫做函式y=f(x)(x∈A)的反函式,記作y=f^-1(x).反函式y=f^-1(x)的定義域、值域分別是函式y=f(x)的值域、定義域。
性質
 反函式
反函式反函式一般具有以下幾種性質:
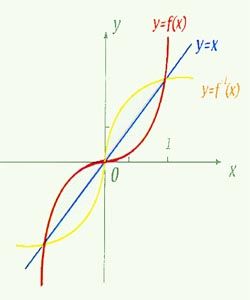
1、互為反函式的兩個函式的圖象關於直線y=x對稱;
2、函式存在反函式的充要條件是,函式在它的定義域上是單調的;
3、一個函式與它的反函式在相應區間上單調性一致;
4、偶函式一定不存在反函式,奇函式不一定存在反函式。若一個奇函式存在反函式,則它的反函式也是奇函式。
5、一切隱函式具有反函式;
6、一段連續的函式的單調性在對應區間內具有一致性;
7、嚴格增(減)的函式一定有嚴格增(減)的反函式【反函式存在定理】。
9、定義域、值域相反對應法則互逆
10、不是所有函式都有反函式如y=x的偶次方
11、反函式的導數關係:如果X=F(Y)在區間I上單調,可導,且F‘(Y)不等於0,那么他的反函式Y=F’(X)在區間S={X|X=F(Y),Y屬於I}內也可導,且[F‘(X)]'=1\[F’(Y)]'。
說明
函式y=f(x)(x∈A)中,設它的值域為C,根據這個函式中x,y的關係,用y把x表示出來,得到x=φ(y).如果對於y在C中的任何一個值,通過x=φ(y),x在A中都有唯一的值和它對應,那么,x=φ(y)就表示y是自變數,x是自變數y的函式,這樣的函式x=φ(y)(y∈C)叫做函式y=f(x)(x∈A)的反函式.
與函式的關係
(1)反函式與函式是相對的。如果函式有反函式,那么函式的反函式就是,即與互為反函式。
(2)與的定義域,值域正好對調。
說明:反函式的定義域是由原函式的值域確定,而不是由它的表達式確定。
存在的條件
按照函式定義,y=f(x)定義域中的每一個元素x,都唯一地對應著值域中的元素y,如果值域中的每一個元素y也有定義域中的唯一的一個元素x和它相對應,即定義域中的元素x和值域中的元素y,通過對應法則y=f(x)存在著一一對應關係,那么函式y=f(x)存在反函式,否則不存在反函式.例如:函式y=x2,x∈R,定義域中的元素±1,都對應著值域中的同一個元素1,所以,沒有反函式。而y=x2,x≥1表示定義域到值域的一一對應,因而存在反函式。
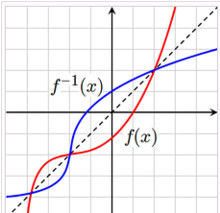
函式與反函式圖象間的關係
函式y=f(x)和它的反函式y=f-1(x)的圖象關於y=x對稱。若點(a,b)在y=f(x)的圖象上,那么點(b,a)在它的反函式y=f-1(x)的圖象上。
簡單命題
(1)一個奇函式y=f(x)如果存在反函式,那么它的反函式y=f-1(x)一定是奇函式.
(2)一個函式在某一區間是增(減)函式,並且存在反函式,那么它的反函式在相應區間也是增(減)函式.
函式y=f(x)
求函式y=f(x)的反函式的一般步驟是:
①確定函式y=f(x)的定義域和值域;
②視y=f(x)為關於x的方程,解方程得x=f-1(y);
③互換x,y得反函式的解析式y=f-1(x);
④寫出反函式的定義域(原函式的值域)。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |