遞歸論

遞歸論，是數理邏輯的一個分支。它是一門研究遞歸涵數及其推廣的學科。遞歸函式是數論函式的一種，其定義域與值域都是自然數集。只是由於構作函式方法的不同而有別於其他的數論涵數。將定義域推廣到不限於自然數集時，便是所謂廣義的遞歸函式。

歷史

　遞歸論這門學科最早可以追溯到原始遞歸式的使用。古代人以及現代的兒童對加法及乘法的理解，實質上就是使用原始遞歸式。但直到17世紀，法國學者B.巴斯加爾才正式使用與遞歸式密切相關的數學歸納法。19世紀德國數學家R.戴德金德和義大利的G.皮亞諾正式使用原始遞歸式,以定義加法與乘法,從而發展了整個自然數論。1923年，T.司寇倫提出並初步證明一切初等數論中的函式都可以由原始遞歸式作出，即都是原始遞歸函式。1931年，K.哥德爾在證明其著名的不完全性定理時，以原始遞歸式為主要工具把所有元數學的概念都算術化了。原始遞歸函式的重要性遂受到人們的重視，人們開始猜測，原始遞歸函式可能窮盡一切可計算的函式。但是，德國數學家W.阿克曼的非原始遞歸的可計算函式的出現，否定了這個猜測，同時也要求人們探討原始遞歸函式以外的可計算函式。1934年，哥德爾在J.赫爾布蘭德的啟示之下，提出了一般遞歸函式的定義；美國的S.C.克利尼則於1936年證明了這樣定義的一般遞歸函式和A.丘奇所定義的λ可定義函式是相同的，並給出了幾種相等價的定義。這樣的一般遞歸函式後來被稱為赫爾布蘭德-哥德爾-克利尼定義。1936年，丘奇、A.M.圖林各自獨立地提出一個論點，即凡可計算的函式都是一般遞歸函式，這就把遞歸函式論與能行性論緊緊地結合起來，從而使遞歸函式的套用範圍大大地擴展了（見能行性與一般遞歸）。關於遞歸函式本身的進展主要在於定義域的推廣,從而得到遞歸字函式、a遞歸函式和遞歸泛涵等等。

基本內容

　遞歸論研究的函式主要包括本原函式、原始遞歸函式、遞歸半函式和遞歸全函式或稱一般遞歸函式、可摹狀函式等等。

本原函式

處處有定義的函式叫做全函式，未必處處有定義的函式叫做半函式或部分函式。最簡單、最基本的函式有三個，即①零函式，O(x)=0,其值永為0；②廣義麼函式或射影函式,Imn(x1,…,xm) =xn(1≤n≤m)；③後繼函式，Sx(=x+1)。這三個函式的合稱就叫做本原函式。 　

　要想由舊函式而作出新函式，必須使用各種各樣的運算元以及疊置。疊置又名複合或代入，它是最簡單、最重要的構造新函式的方法。其一般形式是：由一個 m元函式 f與 m個 n元函式 g1，g2，… ，gm 而造成新函式f【g1(x1,…,xn),g2(x1,…,xn),…,gm(x1,…,xn)】,後者亦可記為f(g1,…,gm)(x1,…,xn)。最常見的造新函式的運算元是原始遞歸式。具有n個參數的原始遞歸式如下：

只有一個參數的原始遞歸式為：

其特點是：不能由A、B兩函式而直接計算新函式的一般值f(u,x)，而只能依次計算f(u,0),f(u,1),f(u,2),…。但只要依次計算，必能把任何一個 f(u,x) 值都算出來。這就是說，只要A、B為全函式且可計算,則新函式f也是全函式且可計算。

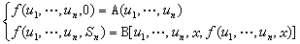
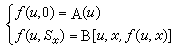
原始遞歸函式

由本原函式出發，經過有限次的疊置與原始遞歸式而作出的函式叫做原始遞歸函式。由於本原函式是全函式且可計算，故原始遞歸函式也是全函式且可計算。原始遞歸函式所涉及的範圍很廣，在數論中所使用的數論函式全是原始遞歸函式。阿克曼卻證明了一個不是原始遞歸的可計算的全函式。經過後人改進後，可表述為如下定義的函式：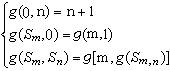

這個函式是處處可以計算的。任給 m,n值,如果m為0,可由第一式算出；如果m不為 0而n為0,可由第二式化歸為求g(m,1)的值，這時第一變目減少了，如果m,n均不為0，根據第三式可先計算g(m,n-1)(設為A),再計算g(m-1,A)，前者g的第二變目減少而第一變目不變,後者則第一變目減少。這樣一步步地化歸,最後必然化歸到第一變目為0，從而可用第一式計算。此外，對任一個一元原始遞歸函式f(x),都可找出一數a使f(x)<g(a,x)。這樣,g(x,x)+1就不可能是原始遞歸函式。
原始遞歸式的推廣，可得到下列有序遞歸式或半遞歸式：

它與原始遞歸式的不同點，在於它不是把 f(u,Sx)的計算化歸於f(u,x,)的計算，而是先化歸於f(u,g(u,Sx))的計算,然後化歸於f【u,g(u,g(u,Sx))】的計算(可寫成f(u,g娾Sx))，再化歸於f(u,g咺Sx)的計算，等等。如果有一個m使得g嚲Sx =0即函式gu在Sx處歸宿於0，那末最後化歸的f(u,g嚲Sx)的計算,將由第一式知f(u,0)=A(u)，依次逐步倒退便可以計算f(u,x)了。如果任何 m均使得g嚲Sx≠0，即函式gu在Sx處不歸宿於0,將導致永遠化歸下去而得不到結果。這樣，不但不能計算 f(u,Sx)，而且它本身根本沒有定義。由此可見,即使A、B與g是處處有定義且可計算的，而由半遞歸式所定義的函式未必是全函式，也可能是半函式。但只要有定義的地方，即gu歸宿於0的地方，就必能計算。

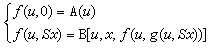
遞歸半函式和遞歸全函式

　從本原函式出發經過有限次的疊置與半遞歸式構成的函式叫做遞歸半函式或遞歸部分函式，也叫做半遞歸函式或部分遞歸函式。這裡所提到的“半”、“部分”不是限制“遞歸”而是限制“函式”的。如果作出的函式是全函式，即其中的gu是處處歸宿於 0的，便叫做遞歸全函式也叫做一般遞歸函式。遞歸半函式的特點是，它可能沒有定義從而沒有值，但只要有值必然可以計算。一般遞歸函式的特點是，它必處處有定義而且處處可以計算。當遞歸半函式沒有定義時，一般是不知道的。這樣，即使把 f(u,Sx)化歸於f(u,gu,Sx)，再化歸於f(u,gu2Sx),…,如此永遠計算下去,也始終得不到其值,並且始終不知道它沒有值。但如果另有辦法判定遞歸半函式是否有值,即是否有定義,情況便大不相同。凡是能夠判定某個遞歸半函式是否有值的，該遞歸半函式叫做潛伏遞歸函式。對潛伏遞歸函式永可在有限步內得出其值，或知道它沒有值，而與一般遞歸函式相同。
另一個重要的構造新函式的方法是造逆函式，例如由加法造減法，由乘法造除法等。設已有函式f（u,x）（只寫一個參數u）就x解方程 f(u,x)=t可得x=g(u,t)，這時函式 g 叫做f（作為 x的函式）的逆函式，可記為g(u,t) = f層(t)，至於解一般的方程f(u,t,x) =0而得x=g(u,t),可以看作求逆函式，即三元函式f的逆的推廣，解方程可以看作使用求根運算元，又叫摹狀運算元。f (u,t,x)=0的最小x根，記為u∝【f(u,t,x) =0】,但當該方程沒有根時,則認為u∝【f(u,t,x) =0】, 沒有定義。因此，即使f(u,t,x)處處有定義且可計算，但使用摹狀運算元後所得的函式u∝【f(u,t,x) =0】仍不是全函式，可為半函式。且只要它有定義,那就必然可以計算。如果f(u,t,x) 本身就是半函式，則u∝【f(u,t,0) =0】的意義是:當f(u,t,x)可計算且其值為0,而x＜n時f(u,t,x)均可計算，且其值非0,則u∝【f(u,t,x) =0】指n。此外的情況均作為無定義看待。 　

可摹狀函式 　

由本原函式出發，經過有限次疊置原始遞歸式與摹狀式而構成的函式叫做可摹狀函式。可摹狀函式一般是部分函式，當摹狀運算元處處有定義時，它才是全函式。但不管是否全函式，凡可摹狀函式有定義的地方都是可計算的。已經證明，可摹狀函式與遞歸半函式是相同的，可摹狀的全函式與一般遞歸函式也是相同的。凡可摹狀函式都可以構作一個圖林機器（見圖林機器理論）計算它，使得當函式有定義時，相應的圖林機器必能終止計算並給出其值；當函式沒有定義時，相應的機器或者停止並給出沒有定義的信號，或者永不停止。由於遞歸函式可以與其性質這樣不同的函式類相等價,因此丘奇和圖林同時提出:可計算函式類恰好是遞歸函式，可計算的半、全函式分別是遞歸半、全函式。他們的這個論點現已受到數理邏輯學界的一致贊同，並被當作能行性理論的一個基礎。