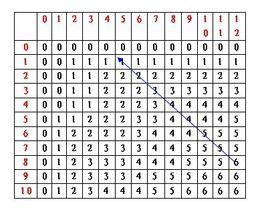
概念介紹
在數學中,某個數列的 子數列是從最初數列通過去除某些元素(有限或無限項)但不破壞餘下元素的相對位置(在前或在後)而形成的新數列。
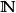 子數列
子數列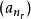 子數列
子數列正式的說,假設X是集合而(a)是X中的數列,這裡的K={1,2,3,...,n},如果(a)是有限數列,且K= ,當(a)是無限數列。則(a)的子數列是形如 的數列,這裡的(n)是在索引集合K中嚴格遞增數列。
定義
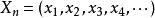 子數列
子數列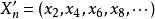 子數列
子數列假設有一條數列 。可以在裡面抽出指定的項組成新的子數列, 。
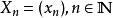 子數列
子數列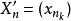 子數列
子數列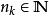 子數列
子數列因為 是自然數,而且它會隨著項數增加而增加,所以它的子數列 , 都會隨著項數增加而增加。
注意:子數列的次序必須和主數列的次序一樣。
例子
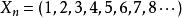 子數列
子數列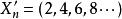 子數列
子數列,只抽出雙數項,就會有子數列, 。
性質
定義一
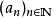 子數列
子數列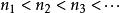 子數列
子數列令 為一實數列及 為一組自然數數列。那么,數列
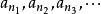 子數列
子數列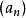 子數列
子數列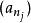 子數列
子數列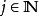 子數列
子數列是的一子數列。其符號表示為,其中是子數列的索引。
證明
 子數列
子數列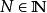 子數列
子數列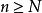 子數列
子數列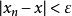 子數列
子數列比任何,根據定理得知,會有一個自然數,所對應的第項符合,。
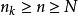 子數列
子數列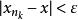 子數列
子數列根據子數列的定義,它都會和所對應的第項符合,。
 子數列
子數列因此,子數列都趨向。
定義二
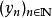 子數列
子數列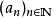 子數列
子數列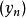 子數列
子數列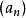 子數列
子數列令及各自為某個數列。那么,是的一子數列,如果:
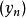 子數列
子數列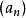 子數列
子數列是由的元素所組成。
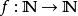 子數列
子數列 子數列
子數列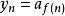 子數列
子數列存在一嚴格遞增函式,使得對所有,。
例子
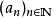 子數列
子數列令為一數列,
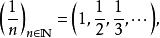 子數列
子數列那么,以下數列
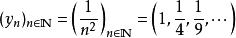 子數列
子數列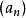 子數列
子數列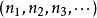 子數列
子數列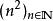 子數列
子數列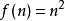 子數列
子數列是的子數列之一。對應定義里的自然數子數列為,而所對應的映射函式為。
參見
•數列
•子數列極限
•上極限和下極限
•Erdős–Szekeres定理