通項公式
遞推公式
斐波那契數列:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
如果設F(n)為該數列的第n項(n∈N*),那么這句話可以寫成如下形式:
顯然這是一個線性遞推數列。
通項公式
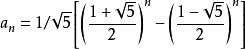 斐波那契數列
斐波那契數列(如上,又稱為“比內公式”,是用無理數表示有理數的一個範例。)
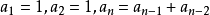 斐波那契數列
斐波那契數列註:此時
通項公式推導
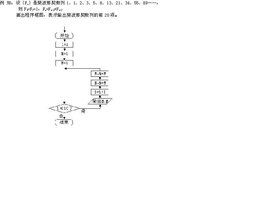 斐波那契數列
斐波那契數列線性遞推數列的特徵方程為:
解得
,
.
則
∵
∴
解得
方法二:待定係數法構造等比數列1(初等代數解法)
 斐波那契數列
斐波那契數列設常數
,
.
 斐波那契數列
斐波那契數列使得
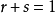 斐波那契數列
斐波那契數列則
,
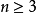 斐波那契數列
斐波那契數列時,有
 斐波那契數列
斐波那契數列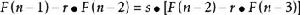 斐波那契數列
斐波那契數列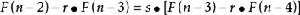 斐波那契數列
斐波那契數列……
 斐波那契數列
斐波那契數列聯立以上n-2個式子,得:
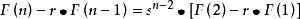 斐波那契數列
斐波那契數列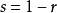 斐波那契數列
斐波那契數列∵
,
上式可化簡得:
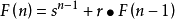 斐波那契數列
斐波那契數列那么
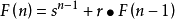 斐波那契數列
斐波那契數列 斐波那契數列
斐波那契數列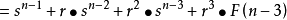 斐波那契數列
斐波那契數列……
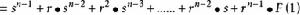 斐波那契數列
斐波那契數列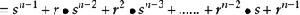 斐波那契數列
斐波那契數列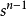 斐波那契數列
斐波那契數列(這是一個以
為首項、以
為末項、
為公比的等比數列的各項的和)。
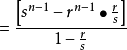 斐波那契數列
斐波那契數列 斐波那契數列
斐波那契數列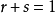 斐波那契數列
斐波那契數列,
的解為
 斐波那契數列
斐波那契數列則
方法三:待定係數法構造等比數列2(初等代數解法)
已知a1=1,a2=1,an=a(n-1)+a(n-2)(n>=3),求數列{an}的通項公式。
解 :設an-αa(n-1)=β(a(n-1)-αa(n-2))。
得α+β=1。
αβ=-1。
構造方程x^2-x-1=0,解得α=(1-√5)/2,β=(1+√5)/2或α=(1+√5)/2,β=(1-√5)/2。
所以。
an-(1-√5)/2*a(n-1)=(1+√5)/2*(a(n-1)-(1-√5)/2*a(n-2))=[(1+√5)/2]^(n-2)*(a2-(1-√5)/2*a1)`````````1。
an-(1+√5)/2*a(n-1)=(1-√5)/2*(a(n-1)-(1+√5)/2*a(n-2))=[(1-√5)/2]^(n-2)*(a2-(1+√5)/2*a1)`````````2。
由式1,式2,可得。
an=[(1+√5)/2]^(n-2)*(a2-(1-√5)/2*a1)``````````````3。
an=[(1-√5)/2]^(n-2)*(a2-(1+√5)/2*a1)``````````````4。
將式3*(1+√5)/2-式4*(1-√5)/2,化簡得an=(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}。
方法四:母函式法。
對於斐波那契數列{a(n)},有a(1)=a(2)=1,a(n)=a(n-1)+a(n-2)(n>2時)
令S(x)=a(1)x+a(2)x^2+……+a(n)x^n+……。
那么有S(x)*(1-x-x^2)=a(1)x+[a(2)-a(1)]x^2+……+[a(n)-a(n-1)-a(n-2)]x^n+……=x
.因此S(x)=x/(1-x-x^2).
不難證明1-x-x^2=-[x+(1+√5)/2][x+(1-√5)/2]=[1-(1-√5)/2*x][1-(1+√5)/2*x].
因此S(x)=(1/√5)*{x/[1-(1+√5)/2*x]-x/[1-(1-√5)/2*x]}.
再利用展開式1/(1-x)=1+x+x^2+x^3+……+x^n+……
於是就可以得S(x)=b(1)x+b(2)x^2+……+b(n)x^n+……
其中b(n)=(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}.
因此可以得到a(n)=b(n)==(1/√5)*{[(1+√5)/2]^n - [(1-√5)/2]^n}
黃金分割
與黃金分割的關係
有趣的是:這樣一個完全是自然數的數列,通項公式卻是用無理數來表達的。而且當n趨向於無窮大時,後一項與前一項的比值越來越逼近黃金分割0.618.(或者說後一項與前一項的比值小數部分越來越逼近黃金分割0.618、前一項與後一項的比值越來越逼近黃金分割0.618)
1÷1=1,2÷1=2,3÷2=1.5,5÷3=1.666...,8÷5=1.6,…………,89÷55=1.6181818…,…………233÷144=1.618055…75025÷46368=1.6180339889…...
越到後面,這些比值越接近黃金比.
與黃金分割的證明
a[n+2]=a[n+1]+a[n]。
兩邊同時除以a[n+1]得到:
a[n+2]/a[n+1]=1+a[n]/a[n+1]。
若a[n+1]/a[n]的極限存在,設其極限為x,
則lim[n->;;∞](a[n+2]/a[n+1])=lim[n->;;∞](a[n+1]/a[n])=x。
所以x=1+1/x。
即x²=x+1。
所以極限是黃金分割比..
相關特性
平方與前後項
從第二項開始,每個奇數項的平方都比前後兩項之積少1,每個偶數項的平方都比前後兩項之積多1。
如:第二項1的平方比它的前一項1和它的後一項2的積2少1,第三項2的平方比它的前一項1和它的後一項3的積3多1。
(註:奇數項和偶數項是指項數的奇偶,而並不是指數列的數字本身的奇偶,比如從數列第二項1開始數,第4項5是奇數,但它是偶數項,如果認為5是奇數項,那就誤解題意,怎么都說不通)
證明經計算可得:[f(n)]^2-f(n-1)f(n+1)=(-1)^(n-1)
與集合子集
斐波那契數列的第n+2項同時也代表了集合{1,2,...,n}中所有不包含相鄰正整數的子集個數。
求和
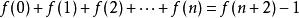 斐波那契數列
斐波那契數列奇數項求和
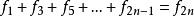 斐波那契數列
斐波那契數列偶數項求和
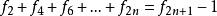 斐波那契數列
斐波那契數列平方求和
 斐波那契數列
斐波那契數列加減求和
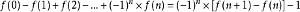 斐波那契數列
斐波那契數列和項數公式
 斐波那契數列
斐波那契數列奇數項與某兩項的平方
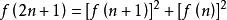 斐波那契數列
斐波那契數列偶數項與某兩項的平方
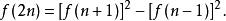 斐波那契數列
斐波那契數列隔項關係
 斐波那契數列
斐波那契數列f(2n-2m-2)[f(2n)+f(2n+2)]=f(2m+2)+f(4n-2m) [ n〉m≥-1,且n≥1]
兩倍項關係
f(2n)/f(n)=f(n-1)+f(n+1)
推廣
斐波那契—盧卡斯數列
盧卡斯數列1、3、4、7、11、18…,也具有斐波那契數列同樣的性質。(我們可稱之為斐波那契—盧卡斯遞推:從第三項開始,每一項都等於前兩項之和f(n) = f(n-1)+ f(n-2)。
盧卡斯數列的通項公式為 f(n)=[(1+√5)/2]^n+[(1-√5)/2]^n
這兩個數列還有一種特殊的聯繫(如下表所示),F(n)*L(n)=F(2n),及L(n)=F(n-1)+F(n+1)
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
| 斐波那契數列F(n) | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | … |
| 盧卡斯數列L(n) | 1 | 3 | 4 | 7 | 11 | 18 | 29 | 47 | 76 | 123 | … |
| F(n)*L(n) | 1 | 3 | 8 | 21 | 55 | 144 | 377 | 987 | 2584 | 6765 | … |
類似的數列還有無限多個,我們稱之為斐波那契—盧卡斯數列。
如1,4,5,9,14,23…,因為1,4開頭,可記作F[1,4],斐波那契數列就是F[1,1],盧卡斯數列就是F[1,3],斐波那契—盧卡斯數列就是F[a,b]。
斐波那契—盧卡斯數列之間的廣泛聯繫
①任意兩個或兩個以上斐波那契—盧卡斯數列之和或差仍然是斐波那契—盧卡斯數列。
如:F[1,4]n+F[1,3]n=F[2,7]n,F[1,4]n-F[1,3]n=F[0,1]n=F[1,1](n-1),
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
| F[1,4]n | 1 | 4 | 5 | 9 | 14 | 23 | 37 | 60 | 97 | 157 | … |
| F[1,3]n | 1 | 3 | 4 | 7 | 11 | 18 | 29 | 47 | 76 | 123 | … |
| F[1,4]n-F[1,3]n | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | … |
| F[1,4]n+F[1,3]n | 2 | 7 | 9 | 16 | 25 | 41 | 66 | 107 | 173 | 280 | … |
②任何一個斐波那契—盧卡斯數列都可以由斐波那契數列的有限項之和獲得,如
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | … |
| F[1,1](n) | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | … |
| F[1,1](n-1) | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | … |
| F[1,1](n-1) | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | … |
| F[1,3]n | 1 | 3 | 4 | 7 | 11 | 18 | 29 | 47 | 76 | 123 | … |
黃金特徵與孿生斐波那契—盧卡斯數列
斐波那契—盧卡斯數列的另一個共同性質:中間項的平方數與前後兩項之積的差的絕對值是一個恆值,
斐波那契數列:|1*1-1*2|=|2*2-1*3|=|3*3-2*5|=|5*5-3*8|=|8*8-5*13|=…=1
盧卡斯數列:|3*3-1*4|=|4*4-3*7|=…=5
F[1,4]數列:|4*4-1*5|=11
F[2,5]數列:|5*5-2*7|=11
F[2,7]數列:|7*7-2*9|=31
斐波那契數列這個值是1最小,也就是前後項之比接近黃金比例最快,我們稱為黃金特徵,黃金特徵1的數列只有斐波那契數列,是獨生數列。盧卡斯數列的黃金特徵是5,也是獨生數列。前兩項互質的獨生數列只有斐波那契數列和盧卡斯數列這兩個數列。
而F[1,4]與F[2,5]的黃金特徵都是11,是孿生數列。F[2,7]也有孿生數列:F[3,8]。其他前兩項互質的斐波那契—盧卡斯數列都是孿生數列,稱為孿生斐波那契—盧卡斯數列。
廣義斐波那契數列
斐波那契數列的黃金特徵1,還讓我們聯想到佩爾數列:1,2,5,12,29,…,也有|2*2-1*5|=|5*5-2*12|=…=1(該類數列的這種特徵值稱為勾股特徵)。
佩爾數列Pn的遞推規則:P1=1,P2=2,Pn=P(n-2)+2P(n-1).
據此類推到所有根據前兩項導出第三項的通用規則:f(n) = f(n-1) * p + f(n-2) * q,稱為廣義斐波那契數列。
當p=1,q=1時,我們得到斐波那契—盧卡斯數列。
當p=1,q=2時,我們得到佩爾—勾股弦數(跟邊長為整數的直角三角形有關的數列集合)。
當p=2,q=-1時,我們得到等差數列。其中f1=1,f2=2時,我們得到自然數列1,2,3,4…。自然數列的特徵就是每個數的平方與前後兩數之積的差為1(等差數列的這種差值稱為自然特徵)。
具有類似黃金特徵、勾股特徵、自然特徵的廣義——斐波那契數列p=±1。
當f1=1,f2=2,p=2,q=0時,我們得到等比數列1,2,4,8,16……
程式編輯
利用這一點,可以用程式編出時間複雜度僅為O(log n)的程式。
怎樣實現呢?偽代碼描述一下
VB語言程式
'**************************************************************
'***函式功能:利用遞歸思想,求解第n項斐波那契數列的值
'***函式名:Fbnq
'***輸入值:n
'***輸入值意義:斐波那契數列的項數
'***返回值:第n項的值
'***時間:2013-01-26 18:46
'***版本:1.0
'**************************************************************
Function Fbnq(n As Integer) As Long '定義函式Fbnq,整型參數n表示要輸出第幾項,返回第n項的值(長整型數據)
Select Case n '對參數進行篩選
Case Is <= 0 '如果n不是自然數
Fbnq = 0 '返回0
Case 1, 2 '如果是第一第二項
Fbnq = 1 '返回1
Case Else '對於第二項以後的
Fbnq = Fbnq(n - 1) + Fbnq(n - 2) '調用遞歸 ,返回前兩項的和
End Select '結束篩選
DoEvents '防止程式崩潰而釋放系統控制權
End Function '函式到此結束
PB語言程式
int li_a,li_b,li_c,i
string ls_print = '~n'
li_b = 1
for i = 1 to 20
li_c = li_a + li_b
li_a = li_b
li_b = li_c
ls_print += "~n" + string(li_c)
next
messagebox("斐波那契數列","前20:"+ls_print)
C語言程式
//利用循環輸出前40項
#include
int main()
{
long fib = {0,1};
int i;
for (i=2;i<41;i++) fib[i] = fib[i-1]+fib[i-2];
for (i=1;i<41;i++) printf("F%d==%d\n",i,fib[i]);
getch();
return 0;
}
//利用遞歸實現指定項輸出
第n項和。
long fib(int n)
{
if (n==0) return 0;
if (n==1) return 1;
if (n>1) return fib(n-1)+fib(n-2);
}
int main()
{
int k=1;
while(k!=0)
{
puts("input a num n 0 for exit");
scanf("%d",&k);
printf("%ld\n",fib(k));
}
getch();
return 0;
}
//高精度斐波那契數列(3000長度的可求到第10000多項)
#include
#include
using namespace std;
int a={};
int b={};
int c={};
int n;
int main()
{
scanf("%d",&n);
if(n<3)
{printf("%d\n",n);
return 0;}
c=2;
b=1;
for(int i=1;i<=n-2;i++)
{for(int j=1;j<=3000;j++)
{a[j]=b[j];
b[j]=c[j];
c[j]=0;}
for(int j=1;j<=3000;j++)
{c[j]=c[j]+a[j]+b[j];
if(c[j]>=10)
{c[j]=c[j]-10;
c[j+1]=1;}
}
}
int i=3000;
while(c[i]==0) i--;
for(i=i;i>=1;i--)
printf("%d",c[i]);
printf("\n");
system("pause");
return 0;
}
C#語言程式
public class Fibonacci
{
//NormRen
static void Main(string[] args)
{
int x = 0,y = 1;
for (int j = 1; j < 10; j++,y = x + y,x = y - x)
Console.Write(y + " ");
}
}
Java語言程式
/*
快速計算第n個Java程式,一秒計算第10萬個數字。
Intel Core2 Duo CPU P8600 2.4GHz 計算第100000個斐波那契數列的數所花時間(毫秒):
第100000:967.8 981.1 988.8 966.3 994.4
*/
public class Fib {
//n為第n個斐波那契數列的數
public static BigInteger compute2(int n) {
if (n == 1 || n == 2) {
return BigInteger.ONE;
}
BigInteger num1 = BigInteger.ONE;
BigInteger num2 = BigInteger.ONE;
BigInteger result = BigInteger.ZERO;
for (int i = 2; i < n; i++) {
result = num1 .add(num2);
num2 = num1;
num1 = result;
}
return result;
}
}
public class Fibonacci
{
public static void main(String[] args)
{
int x=1,y=1;
System.out.println(x+" ");
for(int i=1;i<=20;i++)
{
System.out.println(y+" ");
y=x+y;x=y-x;
}
}
}
Java語言程式(高精度,約一秒鐘計算第20000個數值)
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner s=new Scanner;
int n=s.nextInt();
do{
cul(n);
n=s.nextInt();
}while(n>0);//當n<=0時終止
}
private static void cul(int n) {
BigIntT b=new BigIntT();
BigIntT a=new BigIntT();
b.formatBigInt("1");
a.formatBigInt("2");
if(n==1 || n==2) {
System.out.println⑴;
return;
}
int i=3;
for(;i<=n;i++){
if(i%2>0)
b.add(a);
else
a.add(b);
}
BigIntT t=null;
if(i%2>0) t=b;
else t=a;
for(int j=t.getPos();j<100000;j++)
System.out.print(t.getBase(j));
System.out.println();
}
}
class BigIntT{
int max=100000;
private byte[] base=new byte[max];
private int pos=max;
public void formatBigInt(String arr){
int l=arr.length();
if(l==0) return;
int tmp=l-1;
for(int i=max-1;i>=max-l;i--){
base[i]=(byte) (arr.charAt(tmp--)-'0');
pos--;
}
}
public void add(BigIntT right) {
int bigger=this.getPos()>right.getPos()?right.getPos():this.getPos();
pos=bigger;
for(int i=max-1;i>=pos-2;i--){
int t=this.base[i]+right.getBase(i);
if(t>=10){
this.base[i]=(byte) (t%10);
this.base[i-1]+=t/10;
if(i-1
}else{
this.base[i]=(byte) t;
}
}
}
public int getPos(){
return pos;
}
public byte getBase(int index){
return base[index];
}
}
JavaScript語言程式
function Fibonacci(num){
if(num <= 2){
return 1;
}else{
return Fibonacci(num - 1) + Fibonacci(num - 2)
}
}
遞歸寫法
function fib(n) {
var fib_n = function(curr, next, n) {
if (n === 0) {
return curr;
} else {
return fib_n(next, curr+next, n-1);
}
}
return fib_n(0, 1, n);
}
alert(fib(40));
Pascal語言程式
遞推:
var
b: array[1..40]of longint;
i: integer;
begin
b := 1;
b := 1;
for i:=3 to 40 do
b[i ] := b[i-1] + b[i-2];
for i:=1 to 40 do
write(b[i],' ');
end.
遞歸:
function fib(n:integer):longint;
begin
if (n=1) then exit(0);
if (n=2) then exit⑴;
fib:=fib(n-2)+fib(n-1);
end;
高精度:
program fzu1060;
type arr=array[0..1001]of integer;
var a,b,c:arr;
i,j,k,n:integer;
procedure add(var a,b,c:arr);
begin
fillchar(c,sizeof(c),0);
c:=b;
for i:=1 to c do
c[i]:=a[i]+b[i];
for i:=1 to c do
begin
c[i+1]:=c[i+1]+(c[i] div 10);
c[i]:=c[i] mod 10;
end;
if c[c+1]>0 then
begin
inc(c);
inc(c[c+1],c[c] div 10);
c[c]:=c[c] mod 10;
end;
a:=b; b:=c;
end;
begin
assign(input,'d:\input.txt');
assign(output,'d:\output.txt');
reset(input);
rewrite(output);
while not eof do
begin
readln(n);
fillchar(a,sizeof(a),0);
fillchar(b,sizeof(b),0);
a:=1; a:=1;
b:=1; b:=1;
if n=1 then write⑴
else
if n=2 then write⑴
else
begin
for k:=3 to n do
add(a,b,c);
for k:=c downto 1 do
write(c[k]);
end;
writeln;
end;
close(input);
close(output);
end.
以上程式為 FZU 1060 的標程。
PL/SQL程式
declare i number :=0;
j number :=1;
x number :=1;
begin
while x<1000
loop
dbms_output.put_line(x);
x:=i+j;
i:=j;
j:=x;
end loop;
end;
【Python程式】
# 方法一
def fibonacci(num):
if num <= 2:
f = 1
else:
f=fibonacci(num-1) + fibonacci(num - 2)
return f
例用遞歸方法的計算到第四十項左右,速度就明顯變的緩慢,在python中建議採用列表保存前兩項的方式進行計算。
def fib(x):
l=[]
for i in range(x+1):
if i==0:
continue
elif i==1:
l.append(0)
elif i==2:
l.append(1)
else:
l.append(l[i-2]+l[i-3])
return l
#方法二
import math
def fibonacci1(num):
f = (((math.sqrt⑸ + 1)/2) ** num - ((math.sqrt⑸ - 1)/2) ** num)/math.sqrt⑸
f = round(f,1)
if f - int(f) > 0:
f = int(f) + 1
else :
f = int (f)
return f
【Matlab程式】
function f=fibonacci(n)
p = (1-sqrt⑸)/2 ;
q = (1+sqrt⑸)/2 ;
n=1:n;
f =q.^(n-2)*(1-p).*(1-(p/q).^(n-1))./(1-p/q)+p.^(n-1);
GO語言程式
package main
import "fmt"
import "strconv"
import "os"
func fib(n int) (ret int) {
var b int
if n <3 && n >=0 {
return 1
} else {
b = fib(n-1) + fib(n-2)
return b
}
return
}
func main() {
fmt.Println("fib(4) =:",fib(4))
fmt.Println("fib(5) =:",fib(5))
fmt.Println("fib(6) =:",fib(6)) //(6-1)+(6-2)=
fmt.Println("fib(7) =:",fib(7))
fmt.Println("fib(8) =:",fib(8))
if len(os.Args) > 1 {
if b , err := strconv.Atoi(os.Args); err == nil {
fmt.Println("fib(",os.Args,") =:" ,fib(b))
}
}
}
利用矩陣的實現
時間效率:O(logn),比模擬法O(n)遠遠高效。
代碼(PASCAL)
{變數matrix是二階方陣,matrix是矩陣的英文}
program fibonacci;
type
matrix=array[1..2,1..2] of qword;
var
c,cc:matrix;
n:integer;
function multiply(x,y:matrix):matrix;
var
temp:matrix;
begin
temp[1,1]:=x[1,1]*y[1,1]+x[1,2]*y[2,1];
temp[1,2]:=x[1,1]*y[1,2]+x[1,2]*y[2,2];
temp[2,1]:=x[2,1]*y[1,1]+x[2,2]*y[2,1];
temp[2,2]:=x[2,1]*y[1,2]+x[2,2]*y[2,2];
exit(temp);
end;
function getcc(n:integer):matrix;
var
temp:matrix;
t:integer;
begin
if n=1 then exit(c);
t:=n div 2;
temp:=getcc(t);
temp:=multiply(temp,temp);
if odd(n) then exit(multiply(temp,c))
else exit(temp);
end;
procedure init;
begin
readln(n);
c[1,1]:=1;
c[1,2]:=1;
c[2,1]:=1;
c[2,2]:=0;
if n=1 then
begin
writeln⑴;
halt;
end;
if n=2 then
begin
writeln⑴;
halt;
end;
cc:=getcc(n-2);
end;
procedure work;
begin
writeln(cc[1,1]+cc[1,2]);
end;
begin
init;
work;
end.
數列值的另一種求法:
F(n) = [ (( sqrt ( 5 ) + 1 ) / 2) ^ n ]
其中[ x ]表示取距離 x 最近的整數。
前若干項
⑴1
⑵1
⑶2(1+1)
⑷3(1+2)
⑸5(2+3)
⑹8(3+5)
⑺13(5+8)
⑻21(8+13)
⑼34(13+21)
⑽55(21+34)
⑾89(34+55)
⑿144(55+89)
⒀233(89+144)
⒁377(144+233)
⒂610(233+377)
⒃987(377+610)
⒄1597(610+987)
⒅2584(987+1597)
⒆4181(1597+2584)
⒇6765(2584+4181)
(21)10946(4181+6765)
(22)17711(6765+10946)
(23)28657(10946+17711)
(24)46368(17711+28657)(46368÷28657=0.6180339887 4989484820 4586834......)
......
數列弧線
 斐波那契弧線
斐波那契弧線斐波那契弧線,也稱為斐波那契扇形線。第一,此趨勢線以二個端點為準而畫出,例如,最低點反向到最高點線上的兩個點。然後通過第二點畫出一條“無形的(看不見的)”垂直線。然後,從第一個點畫出第三條趨勢線:38.2%, 50%和61.8%的無形垂直線交叉。
斐波納契弧線,是潛在的支持點和阻力點水平價格。斐波納契弧線和斐波納契扇形線常常在圖表里同時繪畫出。支持點和阻力點就是由這些線的交匯點得出。
要注意的是弧線的交叉點和價格曲線會根據圖表數值範圍而改變,因為弧線是圓周的一部分,它的形成總是一樣的。
社會文明
【艾略特波浪理論】
1946年,艾略特完成了關於波浪理論的集大成之作,《自然法則——宇宙的秘密》。艾略特堅信,他的波浪理論是制約人類一切活動的普遍自然法則的一部分。波浪理論的優點是,對即將出現的頂部或底部能提前發出警示信號,而傳統的技術分析方法只有事後才能驗證。艾略特波浪理論對市場運作具備了全方位的透視能力,從而有助於解釋特定的形態為什麼要出現,在何處出現,以及它們為什麼具備如此這般的預測意義等等問題。另外,它也有助於我們判明當前的市場在其總體周期結構中所處的地位。波浪理論的數學基礎,就是在13世紀發現的費氏數列。
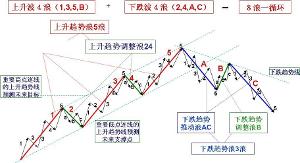 8浪循環圖
8浪循環圖波浪理論數學結構8浪循環圖
·8浪循環圖說明
·波浪理論的推動浪,浪數為5(1、2、3、4、5),調整浪的浪數為3(a\b\c),合起來為8。
·8浪循環中,前5段波浪構成一段明顯的上升浪,其中包括3個向上的衝擊波及兩個下降的調整波。在3個衝擊波之後,是由3個波浪組成的一段下跌的趨勢,是對前一段5浪升勢的總調整。這是艾略特對波浪理論的基本描述。而在這8個波浪中,上升的浪與下跌的浪各占4個,可以理解為艾略特對於股價走勢對稱性的隱喻。
·在波浪理論中,最困難的地方是:波浪等級的劃分。如果要在特定的周期中正確地指認某一段波浪的特定屬性,不僅需要形態上的支持,而且需要對波浪運行的時間作出正確的判斷。
·換句話說,波浪理論易學難精,易在形態上的歸納、總結,難在價位及時間周期的判定。
波浪理論的數字基礎:斐波那契數列
波浪理論數學結構——
斐波那契數列與黃金分割率
·這個數列就是斐波那契數列。它滿足如下特性:每兩個相連數字相加等於其後第一個數字;前一個數字大約是後一個數字的0.618倍;前一個數字約是其後第二個數字的0.382倍;後一個數字約是前一個數字的1.618倍;後一個數字約是前面第二個數字的2.618倍;
·由此計算出常見的黃金分割率為(0.5和1.5外):
0.191、0.236、0.382、0.618、0.809、
1.236、1.382、1.618、1.764、1.809
·黃金分割比率對於股票市場運行的時間周期和價格幅度模型具有重要啟示及套用價值。
黃金分割比率在時間周期模型上的套用
·未來市場轉折點=已知時間周期×分割比率
·已知時間周期有兩種:
⑴循環周期:最近兩個頂之間的運行時間或兩個底之間的運行時間
⑵趨勢周期:最近一段升勢的運行時間或一段跌勢的運行時間
·一般來講,用循環周期可以計算出下一個反向趨勢的終點,即用底部循環計算下一個升勢的頂,或用頂部循環計算下一個跌勢的底。而用趨勢周期可以計算下一個同方向趨勢的終點或是下一個反方向趨勢的終點。
時間循環周期模型預測圖
時間趨勢周期模型預測圖
時間周期與波浪數浪的數學關係
·一個完整的趨勢(推動浪3波或調整浪3波),運行時間最短為第一波(1浪或A浪)的1.618倍,最長為第一波的5.236倍。如果第一波太過短促,則以第一個循環計算(A浪與B浪或1浪與2浪)。
·1.382及1.764的周期一旦成立,則出現的行情大多屬次級趨勢,但行情發展迅速。
·同級次兩波反向趨勢組成的循環,運行時間至少為第一波運行時間的1.236倍。
·一個很長的跌勢(或升勢)結束後,其右底(或右頂)通常在前趨勢的1.236或1.309倍時間出現。
黃金分割比率在價格幅度模型上的套用
·如果推動浪中的一個子浪成為延伸浪的話,則其他兩個推動浪不管其運行的幅度還是運行的時間,都將會趨向於一致。也就是說,當推動浪中的浪3在走勢中成為延伸浪時,則浪1與浪5的升幅和運行時間將會大致趨同。假如並非完全相等,則極有可能以0.618的關係相互維繫。
·浪5最終目標,可以根據浪1浪底至浪2浪頂距離來進行預估,他們之間的關係,通常亦包含有神奇數字組合比率的關係。
·對於ABC調整浪來說,浪C的最終目標值可能根據浪A的幅度來預估。浪C的長度會經常是浪A的1.618倍。當然我們也可以用下列公式預測浪C的下跌目標:浪A浪底減浪A乘0.618。
·在對稱三角形內,每個浪的升跌幅度與其他浪的比率,通常以0.618的神奇比例互相維繫。
黃金分割比率在價格幅度模型上的套用
·0.382:浪4常見的回吐比率、部份浪2的回吐比率、浪B的回吐比率。
·0.618:大部份浪2的調整幅度、浪5的預期目標、浪B的調整比率、三角形內浪浪之間比率。
·0.5:常見是浪B的調整幅度。
·0.236:浪3或浪4的回吐比率,但不多見。
·1.236與1.382:
·1.618:浪3與浪1、浪C與浪A的比率關係。
推動浪形態
·推動浪有五浪構成。第一浪通常只是由一小部分交易者參與的微弱的波動。一旦浪1結束,交易者們將在浪2賣出。浪2的賣出是十分兇惡的,最後浪2在不創新低的情況下,市場開始轉向啟動下一浪波動。浪3波動的初始階段是緩慢的,並且它將到達前一次波動的頂部 (浪1的頂部)。
推動浪浪5未能創新高(低),市場將會出現大逆轉
推動浪的變異形態——傾斜三角形
·傾斜三角形為推動浪中的一種特殊型態(比較少見),主要出現在第5浪的位置。艾略特指出,在股市中,一旦出現一段走勢呈現快速上升或趕底的狀況,其後經常會出現傾斜三角形型態
調整浪形態
·調整是十分難以掌握的,許多艾略特交易者在推動模式階段上賺錢而在調整階段再輸錢。一個推動階段包括五浪。調整階段由三浪組成,但有一個三角形的例外。一個推動經常伴隨著一個調整的模式。
·調整模式可以被分成兩類:
·簡單的調整:之字型調整(N字型調整)
·複雜的調整:平坦型、不規則型、三角形型
調整浪的簡單與複雜調整的交替準則 調整浪的變異形態:強勢三角形
調整浪的變異形態:前置三角形
各段波浪的特性
·在8浪循環中,每段波浪都有不同的特點,熟知這些特點,對波浪屬性的判斷極有幫助,
·第1浪:大部分第1浪屬於營造底部形態的一部份,相當於形態分析中頭肩底的底部或雙底的右底,對這種類型的第1浪的調整(第2浪)幅度通常較大,理論上可以回到第1浪的起點。
小部份第1浪在大型調整形態之後出現,形態上呈V形反轉,這類第1浪升幅較為可觀。在K線圖上,經常出現帶長下影線的大陽線。
從波浪的劃分來說,在5-3-5的調整浪當中,第1浪也可以向下運行,通常第1浪在分時圖上應該顯示明確的5浪形態。
·第2浪:在強勢調整的第2浪中,其回調幅度可能達到第1浪幅度的0.382或0.618,在更多的情況下,第2浪的回調幅度會達到100%,形態上經常表現為頭肩底的右底,使人誤以為跌勢尚未結束。
在第2浪回調結束時,指標系統經常出現超賣、背離等現象。
第2浪成交量逐漸縮小,波幅較細,這是賣力衰竭的表現。
出現傳統系統的轉向信號,如頭肩底、雙底等。
·第3浪:如果運行時間較短,則升速通常較快。在一般情況下為第1浪升幅的1.618倍。如果第3浪升幅與第1浪等長,則第5浪通常出現擴延的情況。
在第3浪當中,唯一的操作原則是順勢而為。因為第3浪的升幅及時間經常會超出分析者的預測。
通常第3浪運行幅度及時間最長。屬於最具爆發性的一浪。大部分第3浪成為擴延浪。第3浪成交量最大。
出現傳統圖表的突破信號,如跳空缺口等。
·第4浪:如果第4浪以平坦型或N字型出現,a小浪與c小浪的長度將會相同。第4浪與第2浪經常是交替形態的關係,即單複式交替或平坦型、曲折型或三角形的交替。
第4浪的低點經常是其後更大級數調整浪中A浪的低點。
經常以較為複雜的形態出現,尤其以三角形較為多見。通常在第3浪中所衍生出來的較低一級的第4浪底部範圍內結束。
第4浪的底不會低於第1浪的頂。
·第5浪:除非發生擴延的情況,第5浪的成交量及升幅均小於第3浪。
第5浪的上升經常是在指標出現頂背離或鈍化的過程中完成。
在第5浪出現衰竭性上升的情況下,經常出現上升楔形形態。這時,成交量與升幅也會出現背離的情況。
如果第1、3浪等長,則第5浪經常出現擴延。如果第3浪出現擴延浪,則第5浪幅度與第1浪大致等長。
市場處於狂熱狀態。
·第6浪A浪:A浪可以為3波或者5波的形態。在A浪以3波調整時,在A浪結束時,市場經常會認為整個調整已經結束。在多數情況下,A浪可以分割為5小浪。
市場人士多認為市場並未逆轉,只視為一個較短暫的調整。
圖表上,陰線出現的頻率增大。
·第7浪B浪:在A浪以3波形態出現的時候,B浪的走勢通常很強,甚至可以超越A浪的起點,形態上出現平坦型或三角形的機率很大。而A浪以5波運行的時候,B浪通常回調至A浪幅度的0.5至0.618。
升勢較為情緒化,維持時間較短。
成交量較小。
·第8浪C浪:除三角形之外,在多數情況下,C浪的幅度至少與A浪等長。
殺傷力最強。
與第3浪特性相似,以5浪下跌。
股價全線下挫。
【人類文明的斐波那契演進】
古老的<馬爾薩斯理論>已經顯靈。馬爾薩斯認為:每當社會財富快速積累,人口快速增長,就會出現:戰爭、瘟疫、饑荒、自然災害來削減人口。2000年科技泡沫達到繁榮的極限,到處都是財富神話!然後盛極而衰,全球經濟急轉直下轉入衰退、長期蕭條。於是:911、阿富汗戰爭、伊拉克戰爭、 SARS、印度洋海嘯、颶風襲擊美利堅、禽流感、寒流襲擊歐羅巴。這一切集中在一起接二連三地發生!2000年是自上世紀30年代全球經濟大蕭條後,一個長達約70年的經濟成長周期的結束點,後面將是一個長期蕭條周期。上世紀30年代全球經濟大蕭條導致了二次世界大戰,被艾略特稱之為:底部戰爭。現在又是一個與上世紀30年代全球經濟大蕭條同級別的經濟蕭條周期,2000年來的經濟蕭條將持續至 2021年才會結束(預測附在下面)。後面是否又會發生被艾略特稱之為的:底部戰爭?至少有不良苗頭:哈馬斯執政、伊朗核問題糾纏,世界將走向何方?
是否還記得那個著名的:
1999年7月之上 (誤差了2年)
恐怖大王從天而降 (911)
使安哥魯摩阿大王為之復活 (美國發動反恐戰爭)
這期間由馬爾斯借幸福之名統治四方 (唯一待驗證)
社會群體心理、群體行為、群體價值觀,乃至國際政治、經濟、軍事,一切皆是自相似系統分形幾何運行階段的反映和結果。
1、自2000年來的全球經濟蕭條將持續至2021年,說明未來將是長期蕭條。
2、之前會有若干次小級別、溫和的經濟擴張和收縮,2010、2011、2018年是拐點。
3、2021年是一個黑暗的年份,人們悲觀、恐懼、絕望的情緒會達到一個極點。到時絕大多數經濟學家會一致悲觀!接著柳岸花明經濟開始復甦,經濟學家們又挨了一記大耳光。
首先,列出一組計算公式:
(公元1937年 – 公元1932年)X 3.618 + 公元1982年 =公元2000年
(公元1966年 – 公元1942年)/1.382 + 公元1982年 = 公元1999年
(公元1837年 – 公元1789年)X 1.382 + 公元1932年 = 公元1998年
(公元1325年 – 公元950年)X 0.618 – (公元1650年 – 公元1490年) + (公元1789年– 公元1650年) + 公元1789年 = 公元2000年
其中:
公元950年 商業革命的起點
公元1325年 商業革命的結束點
公元1490年 資本主義革命的起點
公元1650年 資本主義革命的結束點
公元1789年 工業革命的起點
公元1837年 公元1789年後第一輪經濟擴張的結束點
公元1932年 自公元1929年資本主義世界股災的結束點
公元1937 年 公元1929年股災後第一輪經濟擴張的結束點
公元1942年 公元1929年股災後第二輪經濟擴張的起點
公元1966年 公元1929年股災後第二輪經濟擴張的結束點
公元1982年 70年代全球經濟滯脹的結束點
0.618、1.382、3.618 是斐波那契比率,來源於斐波那契數列
前2個計算公式的含義:
自上世紀30年代資本主義世界經濟大蕭條以來,新的一個自公元1932年開始的上升5浪的經濟擴張周期已經結束,結束點為公元2000年。那么接著是一個調整期(經濟蕭條期),如果是對公元1932年至公元2000年,長度68年的經濟擴張周期的調整,那么它的長度應該比之前小一浪級的第4浪(公元 1966年至公元公元1982年,長16年)要長,那么斐波那契數列中最接近的數字是21年。另外,貝納理論對時間周期的推導,公元2000年為一個重要的高點,公元2003年為一個重要的低點,下一個重要的低點是公元2021年,相互吻合。並且,公元2000年的全球經濟繁榮的拐點、公元2003年的低點已經被全球經濟運行的事實所確認。其中,第2個計算公式誤差了1年。
第3個計算公式的含義:
公元1932年至公元2000年,長度68年的經濟擴張的上升5浪,又是更大浪級一個上升5浪(公元1789年至公元2000年,長度211年)的第5子浪,公元2000年同時又是長211年上升5浪的結束點。該計算公式的結果誤差了2年。那么,接下來的調整(經濟蕭條期)可就不是21年這么短,而是211年的 38.2%、50%、61.8%(斐波那契迴蕩) ,也就是長度幾十年至百年級的。
第4個計算公式的含義:
公元1789年至公元2000年,長211年上升5浪的經濟擴張周期,又是更大浪級公元950年至公元2000年千年浪(浪3)的第5子浪,說明公元 2000年同時又是長度1050年的一個千年浪(浪3)的結束點。那么說明接下來的調整(浪4,經濟蕭條期)將是對千年浪(浪3)的幾百年級的。這種幾百年級規模的調整不得不要從人類文明級別來考慮!之前:古羅馬帝國於公元476年滅亡,之前是一個一千年的羅馬帝國人類奴隸社會的文明(浪1),公元476 年後接著是一個長達474年動盪的、封建的黑暗中世紀(浪2)。並且,公元2000年的拐點(浪3的結束點)已經被全球經濟運行的事實所證實,按照馬爾薩斯的人口理論:每當社會財富快速積累,人口快速增長,就會出現:戰爭、瘟疫、饑荒、自然災害來削減人口。公元2000年後馬爾薩斯理論在不斷被驗證,而唯一還沒有被證實的饑荒,氣候如此大面積劇烈異常波動,難免會造成連續幾年的糧食減產,馬爾薩斯所提到的饑荒也是不難預期地。以後發生的事情還會繼續不斷地驗證馬爾薩斯理論,不信讓你們的孩子的孩子…….....的孩子,來繼續鑑證。(自然災害頻發糧食減產,低素質人口猛超生,已經為將來鬧饑荒打下了伏筆。2007-2-15補)公元2000年一個時間視窗打開,之後將會戰爭、瘟疫、饑荒、自然災害頻發,這個逆流(浪4)的長度將是幾百年長度的,未來的幾百年全球人口將會被消減38.2%或50%或61.8%(斐波那契迴蕩),個人認為38.2%的可能性偏大,也就是說將有大量人口死於非命。即便是沒被消減的,也是活的生不如死。事實已經證明公元2000年是一個千年級的時空
共振點。擴張/收縮、前進/倒退的交替式發展是自然生長、事物發展的自然法則,是不以人的意志為轉移地。況且,人類社會本身就是自然的組成部分。
另外,非常精確的是:
浪3長度是浪2長度的2.236倍(又一個斐波那契比率)
浪3長度= 公元2000年– 公元950年= 1050年
浪2長度= 公元950年– 公元476年= 474年
1050年/2.236 = 470年,與浪2的474年僅很接近,僅誤差4年。
非常巧合的是公元2000年已經被證實是全球經濟運行的重要拐點,同時與上述4個計算公式的計算結果、貝納理論的周期推導結果、還有400多年前的大預言時間出奇的一致!不知道大預言的作者是怎么計算的?
1999年7月之上
恐怖大王從天而降
使安哥魯摩阿大王為之復活
這期間由馬爾斯借幸福之名統治四方
至此我們應該明白,我們偉大的人生處於歷史長河的何種階段?下面的幾百年的調整(浪4),世界將是動盪不安的、到處都充滿仇恨、敵對、剝削、壓迫。有可能會是象偉大革命導師列寧所論述的:資本主義是腐朽的,資本主義是垂死的,無產階級最終是資本主義的掘墓人。人類社會經過幾百年的動盪和無產階級革命(浪4),下一個千年浪(浪5)可能是人類文明的全球普遍社會主義階段,下一個千年浪(浪5)也可能是一個延長浪,其中的第5子浪會上升到共產主義階段,英特納雄耐爾就一定會實現!!
而西方文明精確理論計算的未來:
根據波浪構造指導方針
1、浪2、4趨於等長,或呈斐波那契關係。
2、一個波浪結構中的5個子浪的第1子浪延長,這個波浪結構之後的調整浪幅度將小於等於第2子浪的底。那么,浪4的調整比較可能的是與浪2趨於等長。浪4長度 = 公元950年 – 公元476年 = 474年也就是說,上面提到的公元2000年後的戰爭、瘟疫、饑荒、自然災害頻發來消減人口的逆流(浪4),其長度將持續474年。之後的浪5(社會主義至共產主義文明):浪1、3趨於等長,那么浪5將是延長浪,長度是浪1、3的1.618(斐波那契比率)倍。浪5長度 = (公元2000年 – 公元950年)X 1.618 = 1699年也就是說,西方文明自公元950年來的浪3(發展的驅動浪,它伴隨商業貿易的興起至資本主義的科技泡沫)已於公元2000年結束,之後的浪4(戰亂、瘟疫、饑荒、自然災害頻發的調整浪)將是長度474年的調整,然後的浪5(發展的驅動浪,社會主義至共產主義文明)長度將是1699年,最後西方文明將於公元2000年 + 474年 + 1699年 = 公元4173年結束。
我們人類在地球上的文明史本身可能就是地球生命發展階段的一個子浪而已。
通過對跨度幾千年的中國歷史朝代表分析,驚異地發現中華文明竟然也是以艾略特波浪的斐波那契方式演進!
先看中國封建社會:
浪Ⅰ 公元前221年 --公元220年長度441年 統一、發展的秦、漢
浪Ⅱ 公元220年 -- 公元581年 長度361年 動盪、戰亂、分裂的三國、兩晉、南北朝
浪Ⅲ 公元581年 – 公元907年 長度326年 統一、發展的隋、唐
浪Ⅳ 公元907年 – 公元1279年 長度372年 動盪、戰亂、分裂/並存的五代十國、宋、遼、西夏、金
浪Ⅴ 公元1279年 – 公元1911年 長度632年 統一、發展的元、明、清
並且:
1、中國封建社會的三大盛世“文景之治”、“貞觀之治”、“康乾盛世”就出現在Ⅰ、Ⅲ、Ⅴ三個上升的驅動浪中。
2、浪Ⅴ是延長浪經歷3個朝代,浪Ⅰ、Ⅲ未延長經歷2個朝代。
3、每個驅動浪開頭總有一個短命的朝代:秦、隋、元
4、元/隋 = 89年/37年 = 2.41 隋/秦 = 37年/15年 = 2.47 趨於一致
其間的斐波那契關係:
1、浪Ⅰ長度是浪Ⅲ長度的1.382倍(斐波那契比率),浪Ⅲ長度326年X 1.382 = 451年,與浪Ⅰ長度441年接近。
2、浪Ⅴ長度是浪Ⅰ長度的1.382倍(斐波那契比率),浪Ⅰ長度441年X 1.382 = 609年,與浪Ⅴ長度632年接近。也就是說,(公元220年 – 公元前221年)X 1.382 + 公元1279年 = 公元1888年公式含義:中國封建社會結束點公元1911年之前很多年,就可以通過波浪間的斐波那契關係計算出中國封建社會將於公元1888年結束。只誤差了23年,對於長達2132年的中國封建社會而言,誤差僅為1.08%
3、浪Ⅱ長度是浪Ⅰ長度的0.809倍(斐波那契比率),浪Ⅰ長度441年 X 0.809 =357年,與浪Ⅱ長度361年接近。
4、浪Ⅳ長度372年與浪Ⅱ長度361年趨於等長。
5、浪Ⅴ是延長浪,長度是浪Ⅰ至浪Ⅲ的1.618倍(斐波那契比率)。(441年 – 361年 + 326年)X 1.618 = 657年,與浪Ⅴ長度632年接近。也就是說,(公元220年 – 公元前221年 – 公元581年 + 公元220年 + 公元907年 – 公元581年)X 1.618 + 公元1279年 = 公元1936年
公式含義:
中國封建社會結束點公元1911年之前很多年,就可以通過波浪間的斐波那契關係計算出中國封建社會於公元1936年結束。只誤差了25年,對於長達2132年的中國封建社會而言,誤差僅為1.17%然而公元前221年至公元1911年長達2132年的中國封建社會僅是更大浪級中華文明的第3子浪。
更大浪級的波浪間存在令人瞠目結舌的精確、完美的斐波那契關係:
浪1 約公元前21世紀 -- 公元前722年,長度約1300年,夏、商、周至春秋/戰國前的中國奴隸社會文明。
浪2 公元前722年 -- 公元前221年,長度501年,動盪、戰亂、分裂的春秋/戰國。
浪3 公元前221年 -- 公元1911年,長度2132年,中國封建社會文明。
數列的來源
 斐波那契數列
斐波那契數列 斐波那契數列
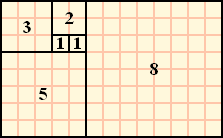
斐波那契數列根據高德納的《電腦程式設計藝術》,1150年印度數學家Gopala和Hemachandra在研究箱子包裝物件長寬剛好為1和2的可行方法數目時,首先描述這個數列。在西方,最先研究這個數列的人是比薩的李奧納多·斐波那契。
斐波那契這個數列來自他的《算盤書》中一道並不出名的問題.他當時寫這道題只是考慮作為一個智力練習.然後,到了19世紀,法國數學家E·盧卡斯出版了一部四卷本的有關娛樂數學方面的著作,把斐波那契的名字,加到該問題的解答和所出現的數列上去。
《算盤書》中引致斐波那契數列的問題是:
1)假定一個月大小的一對兔子(雄和雌的),對於繁殖還太年輕,但兩個月大小的兔子便足夠成熟.又假定從第二個月開始,每一個月它們都繁殖一對新的兔子(雄和雌的)。
2)如果每一對兔子的繁殖都按上面說的同樣的方式,並假定中途沒有兔子死去。試問:從開始起,每個月有多少對兔子呢?
兔子的對數:
很顯然,斐波那契數列的每一項,都等於它前兩項的和。即= +
