基本概念
數列
 數列極限
數列極限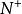 數列極限
數列極限定義 若函式的定義域為全體正整數集合,則稱
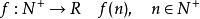 數列極限
數列極限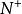 數列極限
數列極限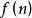 數列極限
數列極限為數列。因正整數集的元素可按由小到大的順序排列,故數列也可寫作
 數列極限
數列極限 數列極限
數列極限 數列極限
數列極限或可簡單地記為,其中稱為該數列的通項。
數列極限
 數列極限
數列極限 數列極限
數列極限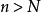 數列極限
數列極限定義設為數列,a為定數。若對任給的正數,總存在正整數N,使得當時有
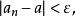 數列極限
數列極限 數列極限
數列極限 數列極限
數列極限則稱數列收斂於a,定數a稱為數列的極限,並記作
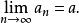 數列極限
數列極限 數列極限
數列極限 數列極限
數列極限 數列極限
數列極限若數列沒有極限,則稱不收斂,或稱發散。
 數列極限
數列極限 數列極限
數列極限 數列極限
數列極限等價定義任給,若在(a-ε,a+ε)之外數列中的項至多只有有限個,則稱數列收斂於極限a。
幾何意義
當n>N時,所有的點xn都落在(a-ε,a+ε)內,只有有限個(至多只有N個)在其外,如右圖1
 圖1
圖1性質
 數列極限
數列極限唯一性 若數列 收斂,則它只有一個極限。
 數列極限
數列極限 數列極限
數列極限 數列極限
數列極限有界性 若數列 收斂,則 為有界數列,即存在正數 ,使得對一切正整數n有
 數列極限
數列極限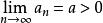 數列極限
數列極限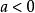 數列極限
數列極限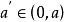 數列極限
數列極限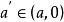 數列極限
數列極限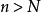 數列極限
數列極限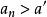 數列極限
數列極限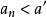 數列極限
數列極限保號性 若 (或 ),則對 (或 ),存在正數N,使得當 時,有 (或 )。
 數列極限
數列極限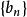 數列極限
數列極限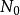 數列極限
數列極限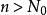 數列極限
數列極限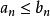 數列極限
數列極限保不等式性 設 與 均為收斂數列。若存在正數 ,使得當 時有 ,則
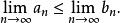 數列極限
數列極限 數列極限
數列極限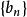 數列極限
數列極限 數列極限
數列極限迫斂性 設收斂數列 , 都以a為極限,數列 滿足:
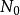 數列極限
數列極限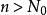 數列極限
數列極限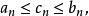 數列極限
數列極限 數列極限
數列極限存在正數 ,當 時有 則數列 收斂,且
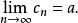 數列極限
數列極限四則運算法則
 數列極限
數列極限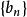 數列極限
數列極限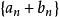 數列極限
數列極限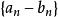 數列極限
數列極限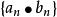 數列極限
數列極限若 與 為收斂數列,則 , , 也都是收斂數列,且有
 數列極限
數列極限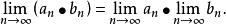 數列極限
數列極限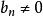 數列極限
數列極限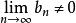 數列極限
數列極限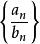 數列極限
數列極限若再假設 及 ,則 也是收斂數列,且有
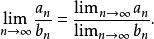 數列極限
數列極限存在的條件
單調有界定理 在實數系中,單調有界數列必有極限。
緻密性定理 任何有界數列必有收斂的子列。
套用
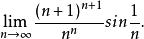 數列極限
數列極限(1)求極限
解:
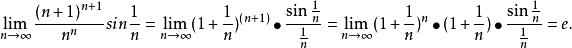 數列極限
數列極限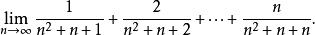 數列極限
數列極限(2)求極限
解:
因為
 數列極限
數列極限 數列極限
數列極限且
 數列極限
數列極限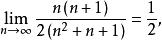 數列極限
數列極限所以,由迫斂性可得
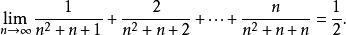 數列極限
數列極限