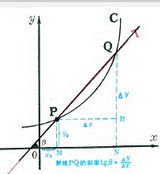
概念
一個變數隨某個變數變化時的速度或變化率;例如路程對於時間的導數便是速度。若變數y 隨變數x 變化的函式關係記為y=ƒ(x),則它在一點x處的導數記為y┡=ƒ┡(x),按定義,它是變化量之比的極限:
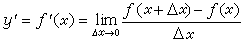 。
。
導數y┡=ƒ┡(x),在函式ƒ(x)可導的範圍內是x的一個函式,稱為函式ƒ(x)的導函式,亦稱導數(見微分學)。
套用
導數的概念構成一種思路,當我們在處理真實世界的問題時,常常遵循這個思路來獲得對於實際對象的性質的刻畫。導數概念具有很強的實際問題的背景,而在實際問題當中總是能夠遇到需要套用導數概念來加以刻畫的概念。由於當初在幾何學問題中,為了要描述斜率這個概念,才啟發人們建立了抽象的一般的導數的概念。比方說在物理學領域,需要大量地套用導數的概念,來刻畫屬於變化率,增長率,強度,通量,流量等等一大類的物理量。例如速度,加速度,電流強度,熱容,等等。在實際問題當中,應該善於提取複雜現象當中所蘊涵的導數概念。
求導公式
 導數
導數運算法則
導數實質上就是一個求極限的過程,導數的四則運算法則來源於極限的四則運算法則。
 導數
導數高階導數
導函式本身就是一個新的函式,應該同樣可以再次對它關於自變數取導數,甚至多次地重複這種步驟,從而得到所謂高階導數。如加速度的概念,就是基於位移對時間的二次導數,二階導數的幾何意義是極其鮮明的,它能反映曲線的凹向。
公式:
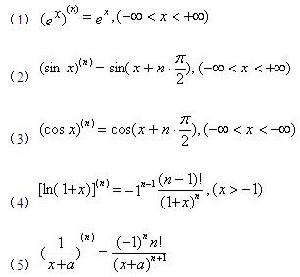 導數
導數以及一個基本求導法則:
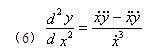 導數
導數經濟套用數學
| 經濟套用數學是高等學校財經類專業的必學內容。此任務主要對微積分的基本知識進行概述講解。提供給剛入門此專業的學生。希望對他們有所幫助。 |
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |