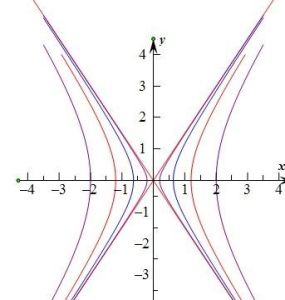
名稱定義
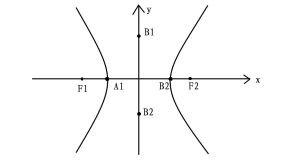 雙曲線
雙曲線即:│PF1-PF2│=2a
定義1:
平面內,到兩個定點的距離之差的絕對值為常數(小於這兩個定點間的距離)的點的軌跡稱為雙曲線。定點叫雙曲線的焦點。
定義2:
平面內,到給定一點及一直線的距離之比為常數e(e=c/a(e>1),即為雙曲線的離心率)的點的軌跡稱為雙曲線。定點叫雙曲線的焦點,定直線叫雙曲線的準線。雙曲線準線的方程為x=±a²/c(焦點在x軸上)或y=±a²/c(焦點在y軸上)。|
定義3:
一平面截一圓錐面,當截面與圓錐面的母線不平行,且與圓錐面的兩個圓錐都相交時,交線稱為雙曲線。
定義4:
在平面直角坐標系中,二元二次方程F(x,y)=ax2+bxy+cy2+dx+ey+f=0滿足以下條件時,其圖像為雙曲線。
1.a、b、c不都是零.
2.b2-4ac>0.
註:第2條可以推出第1條。
在高中的解析幾何中,學到的是雙曲線的中心在原點,圖像關於x,y軸對稱的情形。這時雙曲線的方程退化為:x2/a2-y2/b2=1.
上述的四個定義是等價的,並且根據建好的前後位置判斷圖像關於x,y軸對稱。
標準方程為:
1、焦點在X軸上時為:
x2 /a2 -y2 /b2 =1(a>0,b>0)
2、焦點在Y軸上時為:
y2 /a2 -x2 /b2 =1(a>0,b>0)
特徵介紹
以下從純幾何的角度給出一些雙曲線的相關概念和性質。
分支
可以從圖像中看出,雙曲線有兩個分支。當焦點在x軸上時,為左軸與右軸;當焦點在y軸上時,為上軸與下軸。
焦點
在定義1中提到的兩個定點稱為該雙曲線的焦點,定義2中提到的一給定點也是雙曲線的焦點。雙曲線有兩個焦點。焦點的橫(縱)坐標滿足c²=a²+b²。
準線
在定義2中提到的給定直線稱為該雙曲線的準線。
離心率
在定義2中提到的到給定點與給定直線的距離之比,稱為該雙曲線的離心率。
離心率e=c/a
雙曲線有兩個焦點,兩條準線。(注意:儘管定義2中只提到了一個焦點和一條準線。但是給定同側的一個焦點,一條準線以及離心率可以根據定義2同時得到雙曲線的兩支,而兩側的焦點,準線和相同離心率得到的雙曲線是相同的。)
頂點
雙曲線和它的對稱軸有兩個交點,它們叫做雙曲線的頂點。
實軸
兩頂點之間的距離稱為雙曲線的實軸。實軸長的一半稱為實半軸。
漸近線
雙曲線有兩條漸近線。漸近線和雙曲線不相交。
漸近線的方程求法是:將右邊的常數設為0,即可用解二元二次的方法求出漸近線的解,例如:X2 /2-Y2 /4=1,令1=0,則X2 /2=Y2 /4,則雙曲線的漸近線為Y=±(√2)X
一般地我們把直線Y=±(b/a)X叫做雙曲線的漸進線(asymptotetothehyperbola)(焦點在X軸上)
焦點在y軸上直線為Y=±(a/b)X
頂點連線斜率
雙曲線x2/a2-y2/b2=1上一點與兩頂點連線的斜率之積為b2/a2。
實際套用
雙曲線在實際中的套用有通風塔,冷卻塔,艾菲爾鐵塔,廣州塔等。
面積公式編輯
若∠F1PF2=θ,
則S△F1PF2=b2 ×cot(θ/2)或S△F1PF2=b2 /tan(θ/2)
例:已知F1、F2為雙曲線C:x2-y2=1的左右焦點,點P在C上,∠F1PF2=60°,則P到x軸的距離為多少?
解:由雙曲線焦點三角形面積公式得:
S△F1PF2=b2 ×cot(θ/2)=√3
設P到x軸的距離為h,則S△F1PF2=1/2×h×2√2;h=√6/2[4]參數方程絕對值
光學性質
從雙曲線一個焦點發出的光,經過雙曲線反射後,反射光線的反向延長線都匯聚到雙曲線的另一個焦點上。雙曲線這種反向虛聚焦性質,在天文望遠鏡的設計等方面,也能找到實際套用。
盤點高中數學名詞
| 高中是大學的過渡階段,學好高中數學,才能為學好大學數學打好基礎,那我們盤點下高中數學中有哪些名詞吧。 |