引入
在一元函式中,導數就是函式的變化率。對於二元函式研究它的“變化率”,由於自變數多了一個,情況就要複雜的多。
在 xOy 平面內,當動點由 P(x,y) 沿不同方向變化時,函式 f(x,y) 的變化快慢一般來說是不同的,因此就需要研究 f(x,y) 在 (x,y) 點處沿不同方向的變化率。
在這裡我們只學習函式 f(x,y) 沿著 平行於 x 軸和 平行於 y 軸兩個特殊方位變動時, f(x,y) 的變化率。
偏導數的表示符號為:∂。
偏導數反映的是函式沿坐標軸正方向的變化率。
定義
x方向的偏導
設有二元函式 z=f(x,y) ,點(x,y)是其定義域D 內一點。把 y 固定在 y而讓 x 在 x 有增量 △x ,相應地函式 z=f(x,y) 有增量(稱為對 x 的偏增量)△z=f(x+△x,y)-f(x,y)。
如果 △z 與 △x 之比當 △x→0 時的極限存在,那么此極限值稱為函式 z=f(x,y) 在 (x,y)處對 x 的偏導數,記作 f'(x,y)或。函式 z=f(x,y) 在(x,y)處對 x 的偏導數,實際上就是把 y 固定在 y看成常數後,一元函式z=f(x,y)在 x處的導數。
y方向的偏導
同樣,把 x 固定在 x,讓 y 有增量 △y ,如果極限存在那么此極限稱為函式 z=(x,y) 在 (x,y)處對 y 的偏導數。記作f'(x,y)。
求法
當函式 z=f(x,y) 在 (x,y)的兩個偏導數 f'(x,y) 與 f'(x,y)都存在時,我們稱 f(x,y) 在 (x,y)處可導。如果函式 f(x,y) 在域 D 的每一點均可導,那么稱函式 f(x,y) 在域 D 可導。
此時,對應於域 D 的每一點 (x,y) ,必有一個對 x (對 y )的偏導數,因而在域 D 確定了一個新的二元函式,稱為 f(x,y) 對 x (對 y )的偏導函式。簡稱偏導數。
按偏導數的定義,將多元函式關於一個自變數求偏導數時,就將其餘的自變數看成常數,此時他的求導方法與一元函式導數的求法是一樣的。
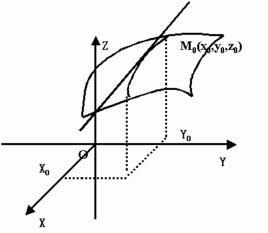
幾何意義
表示固定面上一點的切線斜率。
偏導數 f'(x,y) 表示固定面上一點對 x 軸的切線斜率;偏導數 f'(x,y) 表示固定面上一點對 y 軸的切線斜率。
高階偏導數:如果二元函式 z=f(x,y) 的偏導數 f'(x,y) 與 f'(x,y) 仍然可導,那么這兩個偏導函式的偏導數稱為 z=f(x,y) 的二階偏導數。二元函式的二階偏導數有四個:f",f",f",f"。
注意:
f"與f"的區別在於:前者是先對 x 求偏導,然後將所得的偏導函式再對 y 求偏導;後者是先對 y 求偏導再對 x 求偏導。當 f"xy 與 f"yx 都連續時,求導的結果與先後次序無關。