廣義導數

廣義導數是一個數學概念，20世紀70年代相繼出現了各種廣義導數的概念。

2O世紀7O年代相繼出現了各種廣義導數（Generalized Derivatives）的概念。廣義導數的定義與支集、δ函式的概念密切相關。為此，先給出一些預備的知識。

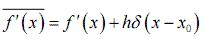
支集

■　f(x)的支集是指：spt(f)={x∈R|f(x)≠0}
■　C∞(R)表示：具有緊支集且無限次可微函式組成的空間
定義 1　設Fn(x)∈C∞(R)，若滿足：
（1）存在緊集K，使得spt (Fn(x)) 包含在K內；
（2）對於任意的a>0，limsup|T^{(a)} (Fn(x)-F(x))|=0;
稱 Fn(x)-->F(x) on C∞(R) (當n->∞)

廣義函式

定義 2　記D*(R)={F(x)∈C∞(R) | 存在Fn(x)∈C∞(R)，s.t. Fn(x)-->F(x) (n-->∞)}
定義 3 設f在R上局部可積（即對任意緊集K，∫_{K} |f(x)|dx<∞)
則f(x)確定了一個D*(R)的廣義函式T_f：
T_f(F)=<f,F>=∫_{R} f(x)F(x)dx (對任意F∈D*(R))
定義 4 (δ函式)　T_δ(F)=∫_{R} δ(x)F(x)dx=δ(0) (對任意F∈D*(R))

廣義導數

定義 5　設 f(x)在x=x0有一類間斷點，躍度為h,
若 其常義導數f&#039;(x)在R\{x0}上連續，
則 其廣義導數D_f(x)=f&#039;(x)+hδ(x-x0).

舉例

例如　已知　Sgn(x)=x/|x|，則
常義導數為：sgn&#039;(x)=0 (x≠0)
廣義導數為：D_{sgn} (x)=2δ(x)