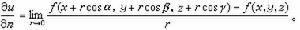定義
 方嚮導數
方嚮導數 方嚮導數
方嚮導數 方嚮導數
方嚮導數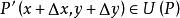 方嚮導數
方嚮導數 方嚮導數
方嚮導數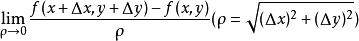 方嚮導數
方嚮導數 方嚮導數
方嚮導數 方嚮導數
方嚮導數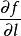 方嚮導數
方嚮導數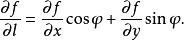 方嚮導數
方嚮導數設函式z=f(x,y) 在點P(x,y)的某一鄰域U(P)內有定義,自點P引射線 ,自x軸的正向到射線 的轉角為 , 為 上的另一點,若 存在,則稱此極限值為 在點P沿方向 的方嚮導數,記作 .其計算公式為
 方嚮導數
方嚮導數 方嚮導數
方嚮導數三元函式u=f(x,y,z)在點P(x,y,z)沿著方向 (方向角為 )的方嚮導數的定義為
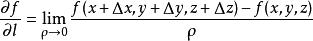 方嚮導數
方嚮導數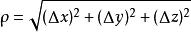 方嚮導數
方嚮導數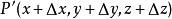 方嚮導數
方嚮導數 方嚮導數
方嚮導數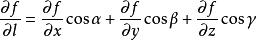 方嚮導數
方嚮導數其中 且 為 上的點,其計算公式為 .
沿直線方向
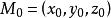 方嚮導數
方嚮導數 方嚮導數
方嚮導數設 為數量場u=u(M) 中的一點,從點 出發引一
 方嚮導數
方嚮導數 方嚮導數
方嚮導數 方嚮導數
方嚮導數 方嚮導數
方嚮導數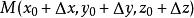 方嚮導數
方嚮導數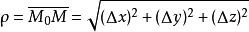 方嚮導數
方嚮導數 方嚮導數
方嚮導數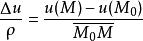 方嚮導數
方嚮導數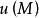 方嚮導數
方嚮導數 方嚮導數
方嚮導數 方嚮導數
方嚮導數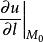 方嚮導數
方嚮導數條射線 (其方向用 表示),在 上點 的鄰近取一動點 ,記 ,如圖所示,若當 時,分式 的極限存在,則稱它為函式 在點 處沿 方向的方嚮導數,記作 ,即
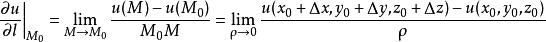 方嚮導數
方嚮導數 沿直線的方嚮導數
沿直線的方嚮導數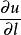 方嚮導數
方嚮導數 方嚮導數
方嚮導數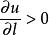 方嚮導數
方嚮導數 方嚮導數
方嚮導數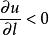 方嚮導數
方嚮導數 方嚮導數
方嚮導數方嚮導數 是在點M 處函式u(M) 沿方向 的對距離的變化率.故(1)當 時,函式u 沿 方向就是增加的;(2)當 時,函式u 沿 方向就是減少的.
在直角坐標系中,方嚮導數由下面定理給出計算公式。
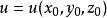 方嚮導數
方嚮導數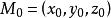 方嚮導數
方嚮導數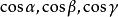 方嚮導數
方嚮導數 方嚮導數
方嚮導數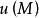 方嚮導數
方嚮導數 方嚮導數
方嚮導數 方嚮導數
方嚮導數1.若函式 在點 處可微, 為 方向的方向餘弦,則函式u 在點 處沿 方向的方嚮導數必存在,且滿足
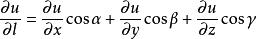 方嚮導數
方嚮導數 方嚮導數
方嚮導數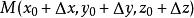 方嚮導數
方嚮導數證,設動點 的坐標為
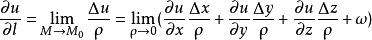 方嚮導數
方嚮導數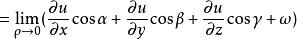 方嚮導數
方嚮導數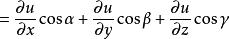 方嚮導數
方嚮導數 方嚮導數
方嚮導數 方嚮導數
方嚮導數 方嚮導數
方嚮導數 方嚮導數
方嚮導數2.若在有向曲線C上取一定點 作為計算弧長s的起點,若以C的正向作為s增大的方向;M為C上的一點,在點M處沿C的正向作一與C相切的射線 (其方向用 表示),則當函式u可微、曲線C光滑時,u在點M處沿 方向的方嚮導數就等於u對s的全導數,即
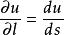 方嚮導數
方嚮導數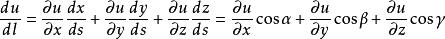 方嚮導數
方嚮導數證,曲線C是光滑的,其參數方程為x=x(s),y=y(s),z=z(s),函式u=u[x(s),y(s),z(s)],
沿曲線方向
 方嚮導數
方嚮導數 方嚮導數
方嚮導數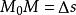 方嚮導數
方嚮導數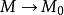 方嚮導數
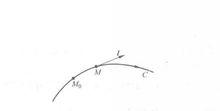
方嚮導數如圖所示,設 為數量場u=u(M)中曲線C上的一點,在點 的鄰近取一動點M,記 ,若當 時,分式
 沿曲線方向的方嚮導數
沿曲線方向的方嚮導數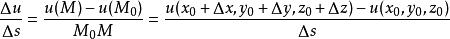 方嚮導數
方嚮導數 方嚮導數
方嚮導數的極限存在,則稱它為函式u(M)在點 處沿曲線(正向)方向的方嚮導數,記作
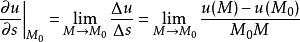 方嚮導數
方嚮導數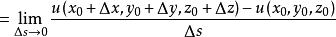 方嚮導數
方嚮導數當曲線C光滑時,在點M處函式u可微,函式u沿C方向的方嚮導數就等於u對s的全導數,則有
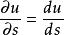 方嚮導數
方嚮導數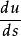 方嚮導數
方嚮導數證 因為當曲線C光滑時,在點M處函式u可微,故全導數 存在.
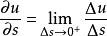 方嚮導數
方嚮導數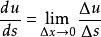 方嚮導數
方嚮導數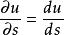 方嚮導數
方嚮導數,當 存在時,有 。
 方嚮導數
方嚮導數推論 若曲線C 光滑時,在點M處函式u可微,函式u在點M處沿C方向的方嚮導數就等於函式u在點M處沿C的切線方向 (C正向一側)的方嚮導數,即
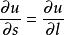 方嚮導數
方嚮導數