定理證明
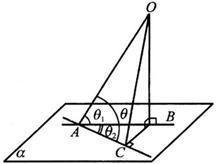
如上圖,已知OA是面α的一條斜線,OB⊥α。在α內過B作BC⊥AC,垂足為C,連線OC。OA和α所成角∠OAB=θ1,AC和AB所成角∠BAC=θ2,OA和AC所成角∠OAC=θ。求證cosθ=cosθ1*cosθ2
證明:
∵OB⊥α
∴BC是OC在α上的射影
∵BC⊥AC
∴OC⊥AC(三垂線定理)
由三角函式的定義可知
cosθ1=AB/OA,cosθ2=AC/AB,cosθ=AC/OA
∴cosθ1*cosθ2=AB/OA*AC/AB=AC/OA=cosθ
或利用三面角餘弦定理來證明。
在三面角A-OBC中,設二面角O-AB-C為∠AB,易證∠AB=90°
由三面角餘弦定理得
cos∠OAC=cos∠OAB*cos∠CAB+sin∠OAB*sin∠CAB*cos∠AB
即cosθ=cosθ1*cosθ2+sinθ1*sinθ2*cos90°=cosθ1*cosθ2
定理說明
雖然在證明該定理的過程中,平面內的直線AC經過斜線AO和α的交點A(斜足),但實際上在α內任何一條與AC平行的直線l,都可以經過平移使得l和AC重合。而一旦l不經過點A,則l和OA互為異面直線(平面的一條斜線和平面內不經過斜足的直線互為異面直線),根據異面直線所成角的定義,l和OA所成角即為∠OAC。也就是說,利用該定理可以很方便地求出異面直線所成角。
定理套用
如果將三餘弦定理和三正弦定理聯合起來使用,用於解答立體幾何綜合題,你會發現出乎意料地簡單,甚至不用作任何輔助線!
例1 如圖,已知A1B1C1-ABC是正三稜柱,D是AC中點,若AB1⊥BC1,求以BC1為棱,DBC1與CBC1為面的二面角α的度數.(1994年全國高考理科數學23題)
 三餘弦定理套用例題1解答
三餘弦定理套用例題1解答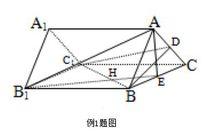 三餘弦定理套用例題1
三餘弦定理套用例題1例2 已知Rt△ABC的兩直角邊AC=2,BC=3.P為斜邊AB上一點,現沿CP將此直角三角形折成直二面角A-CP-B(如下圖),當AB=√7時,求二面角P-AC-B大小.(上海市1986年高考試題,難度係數0.28)
 三餘弦定理套用例題2解答
三餘弦定理套用例題2解答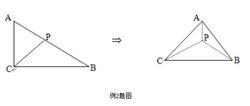 三餘弦定理套用例題2
三餘弦定理套用例題2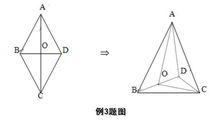 三餘弦定理套用例題3
三餘弦定理套用例題3 三餘弦定理套用例題3解答
三餘弦定理套用例題3解答例3.已知菱形ABCD的邊長為1,∠BAD=60°,現沿對角線BD將此菱形折成直二面角 A-BD-C(如圖6).( 1)求異面直線AC與BD所成的角;( 2)求二面角A-CD-B的大小.