發展歷史
有限群論是 群論的基礎部分,也是群論中套用最為廣泛的一個分支。歷史上,抽象群論的許多概念起源於有限群論。近年來,隨著有限群理論的迅速發展,其套用的日益增多,有限群論已經成為現代科技的數學基礎之一,是一般科技工作者樂於掌握的一個數學工具。有限群論無論是從理論本身還是從實際套用來說,都占有突出地位,它中的置換群、可解和非可解群、冪零群、以及群表示論等等,都是重要的研究對象,總之,其內容十分豐富而且龐大。
有限群的研究起源很早,其形成時期是與 柯西、 拉格朗日、 高斯、 阿貝爾以及後來的伽羅瓦、若爾當等人的名字相聯繫的。1829年 伽羅瓦(Galois)引入了置換群的概念,並成功地解決了一個方程可用根式求解的充要條件。置換群是群論歷史上最先知道的一種具體的群。拉格朗日和高斯在研究數論中的二次型類是出現過交換群的概念;Cayley(凱萊)曾經在1849年提出過抽象群,但這個概念的價值當時沒有被認識到,遠遠超越時代的Dedekind(戴德金)在1858年給有限群下了一個抽象的定義,這個群是從置換群中引導出來的,他又在1877年提出了一個抽象的有限交換群。Kronecker(克羅內克)也給出了一個相當於阿貝爾群的定義,他規定了抽象的元素,運算,封閉性,結合性,交換性。以每個元素的逆運算的存在和唯一。他還證明了一些有關群的定理。1878年又是凱萊提出了一個群可以看作一個普遍的概念。毋需只限於置換群,這樣認識到抽象群比置換群包含更多的東西。德國數學家霍爾德在l889年以後的若干年內,詳細地研究了單群和可解群,證明:一個素數階循環群是單群,n個(n>=5)文字的全部偶置換組成的交換群是單群。他還發現了許多其他有艱的單群。赫爾德和若爾當還建立了在有限群中的若爾當一霍爾德合成群列和若爾當一霍爾德定理。在19世紀末,德國數學家弗羅貝尼烏斯、迪克和英國數學家伯恩塞德等都致力於可解群的研究。20世紀初伯恩塞德證明的關於 (p,q是素數)必是可解群的定理,導致了對有限單群進行分類的重要研究。美國數學家湯普森和菲特在20世紀60年代初證明了有限群中長期懸而未決的一個猜想(伯恩塞德猜想);奇數階群一定是可解群。它推動了有限群理論的發展。有限單群的完全分類,即找出有限單群所有的同構類,經過上百名數學家約百年的共同努馬中騏.群論習題精解1981年得到解決,這是數學史上的一個非凡成就。
說明
設G是一個 群, 如果G是 有限 集合,那么就稱為有限群。
假若群G是一個有限群,則成G的元的個數位G的階,記為 |G|。
有限群的分類是個重要的數學問題。這個問題經過許多數學家的努力中有了完美的答案(相關概念如“魔群”)。
比如 素數階的有限群都是 循環群。
5階分類
Z表示循環群,S表示置換群,A表示交錯群,D表示二面群,×表示直積。
| 階數 | 交換群 | 非交換群 |
| 1 | 平凡群, Z1 = S1 = A2 | |
| 2 | Z2 = S2 = D1 | |
| 3 | Z3 = A3 | |
| 4 | Z4 | |
| 克萊因四元數群, Z2^2 | | |
| 5 | Z5 | |
| 6 | Z6 = Z3 × Z2 | S3 = D3 |
| 7 | Z7 | |
| 8 | Z8 | D4 |
| Z4 × Z2 | 四元數群Q8 | |
| Z2^3 | | |
| 9 | Z9 | |
| Z3^2 | | |
| 10 | Z10 = Z5 × Z2 | D5 |
| 11 | Z11 | |
| 12 | Z12 = Z4 × Z3 | D6 = D3 × Z2 |
| Z6 × Z2 = Z3 × Z2^3 | A4 | |
| | 第3個Dicyclic群 | |
| 13 | Z13 | |
| 14 | Z14 = Z7 × Z2 | D7 |
| 15 | Z15 = Z5 × Z3 | |
群中長期懸而未決的一個猜想,奇數階的群一定是可解群,因而有限非交換單群的階必為偶數。
正文
(見群、有限單群)。
可解群如果有限群
之合成群列
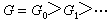 有限群
有限群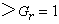 有限群
有限群的每個商群
/
(稱為
的合成商因子)是交換群,那么有限群
稱為可解群。易知,若
的合成商因子
/
是交換群,則必為素數階的循環群。所謂
的合成群列,是指在
中由有限多個子群組成的降鏈如
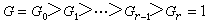 有限群
有限群,使得
是
的極大正規子群,即
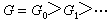 有限群
有限群,且凡滿足
<
<
的
不再是
的正規子群。
的任意兩個合成群列是等價的,意即如果
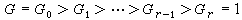 有限群
有限群與
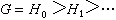 有限群
有限群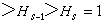 有限群
有限群是
的任意兩個合成群列,那么必有s=
,且
個商群
/
,
/
,…,
/
(即
)分別與
個商群
/
,
/
,…,
/
(即
)除次序外是兩兩互相同構的。易證,由合成群列
=
>
>…>
=1所成的每個商群是單群。
在群
中由有限多個正規子群組成的降鏈
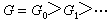 有限群
有限群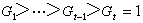 有限群
有限群使
為真包含於
內的
之極大正規子群(即
/
是
/
的極小正規子群),稱為
的主群列。
的任意兩個主群列是等價的。其等價定義與合成群列的等價定義相同。
有限群有合成群列或主群列存在,且任意兩個合成群列或主群列是等價的。這就是若爾當-赫爾德-施賴埃爾定理。凡是階等於
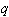 有限群
有限群ъ的群恆為可解群,其中
、
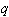 有限群
有限群是互異的素數,
、
是非負整數。這就是著名的伯恩賽德定理。而W.費特、J.湯普森在20世紀60年代初期又證明了有限群中長期懸而未決的一個猜想,奇數階的群一定是可解群,因而有限非交換單群的階必為偶數。
西洛性質有限群理論中一個經典而重要的結果是著名的拉格朗日定理:有限群
的階│
│等於
的子群
的階│
│與
在
內的指數│
:
│的乘積,即│
│=│
│·│
:
│。但是,並非對│
│的任何因數
,
一定有階為
的子群。例如,四次交錯群
的階為12,而
沒有6階子群(見置換群)。當│
│的因數是
形的數即一素數
的
次冪時,則
必有階為
的子群。這就是有名的西洛第一定理。若除盡│
│的
的最高次冪是
,其中
是素數,m是自然數,則
的
階子群稱為西洛
子群。所謂西洛第二定理,其意為:①
中任兩個西洛
子群在
內是共軛的;②
中西洛
子群的個數
,必滿足
呏1(mod
),且為任一西洛
子群的正規化子在
內的指數;③
中凡是階為
的子群必為某西洛
子群的子群。進一步有關於有限可解群的西洛基定理:
為可解群的充分必要條件是
有一組西洛基
,
,…,
,使
=
…
。所謂西洛基,是指當
的階
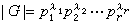 有限群
有限群(素因數分解)時,
的一組西洛
子群
,
=1,2,…,
,且
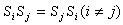 有限群
有限群,使
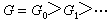 有限群
有限群。可解群的西洛基往往不止一組,但是,可解群的任意兩組西洛基
,
,…,
與
,
,…,
是等價的,即在
中必有元素
使
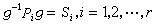 有限群
有限群。階為素數冪的群,習慣上稱為
群。西洛子群都是
群。有限可解群可以表為
群之積。西洛第一定理和第二定理統稱為西洛定理。在有限可解群中可得到西洛定理推廣的結果:有限群
為可解群的充分必要條件是,只要有分解│
│=m
,(m,
)=1,
就有階為m的子群;當
是可解群時,凡是階為m的子群必互為共軛,若m
│m,則
中凡是階為m
的子群必為
中至少一個階為m的子群的子群。這樣的m階子群,通常稱為可解群
中的霍爾π子群。
所謂群的π 性質,意即西洛性質的推廣。西洛性質是西洛定理的同義語, 即如果有限群
的階|
|=
,
│
,(
,
/
)=1,
為素數冪,那么
至少有一個
階子群,且任意兩個
階子群是共軛的,而
中凡是以
的因數為階的子群,一定是
中某個
階子群的子群。P.霍爾去掉上述條件中的“
為素數冪”而設“
是可解群”並得到了同樣的結論。於是,根據P.霍爾的這一思想方法,將“
為素數冪”改為其他條件來進行探索的工作頗多。例如,“
為素數冪”改為“
包含一個
階冪零子群”,仍得到相應的結論,即古典的西洛定理推廣到含有
的一切素因數的集合π上所得的結果。
冪零群當可解群
的西洛基中諸西洛子群都是正規子群時,則可解群
稱為冪零群。冪零群是可解群中的一個子類。有限群
為冪零群的充分必要條件是,
可表為
群的直積。
群自身當然是冪零群。除了這個充分必要條件外,還有幾個互為等價的充分必要條件,其中最重要的是,
有上中心列或下中心列。所謂上中心列,是指
有長為m的子群列
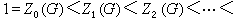 有限群
有限群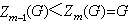 有限群
有限群,使
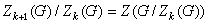 有限群
有限群,且其中 Z
(
)為
的中心Z(
),而遞歸地給出Z
(
)使
Z
(
)/Z
(
)是商群
/Z
(
)的中心。由
的限性可知,必有某自然數
使
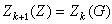 有限群
有限群,因此當m≥
時, 恆有Z
(
)=Z
(
)。特別地,有某m使Z
(
)=
。所謂下中心列,是指
有長為
的子群列
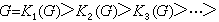 有限群
有限群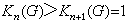 有限群
有限群。設
、
是
的任意兩個子集,【
,
】表示由形如
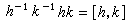 有限群
有限群的元素所生成的
的子群,即【
,
】=<【
,
】│
∈
,
∈
>,於是【
,
】=【
,
】。當【
,…,
】定義後,再遞歸地定義
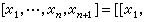 有限群
有限群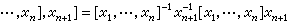 有限群
有限群。同樣,對
的子集
,…,
也作類似的定義
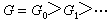 有限群
有限群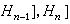 有限群
有限群,且當任意
∈
(
=1,2,…,
)時,則定義
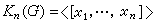 有限群
有限群,因此
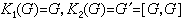 有限群
有限群,且
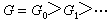 有限群
有限群。易知
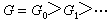 有限群
有限群。從
的有限性可知,有某自然數
使
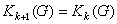 有限群
有限群。因此當m≥
時恆有
(
)=
(
)。特別地,有自然數
使
(
)=1。有限群的上中心列和下中心列兩者同時存在,且其長相等, 此時
必為冪零群,稱為
類冪零群。因而,1類冪零群就是交換群。由此可知,冪零群是介於交換群與可解群之間的一類群。冪零群有下中心列,可解群則有換位群列。
為可解群的充分必要條件是,
有換位群列。所謂換位群列,是指
的子群列
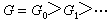 有限群
有限群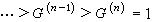 有限群
有限群,式中
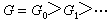 有限群
有限群為
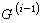 有限群
有限群的換位子群,即
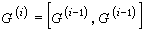 有限群
有限群,而
是某一正整數。此時
也稱為
步可解群。1步可解群就是交換群。
群 在有限群的研究中,
群具有重要的意義。互不同構的
階群究竟有多少個,是一個古老而艱難的問題。迄今只解決了當
為奇素數且
≤6時以及當
=2且
≤7時
階群的個數問題。關於
群方面的工作頗多,其中由P.霍爾發表的計數原理與正則
群是奠基性的工作。所謂計數定理,例如,設|
|=
,
(
)表示
中
階子群的個數,其中0≤
≤
。當
(
)=1(1<
<
)時,則
必是循環群;當
(
)=1時;則
或為循環群或可能為所謂廣義四元數群,後者僅在
=2及
≥3時可能出現;對於0≤
≤
,有
(
)呏1(mod
)。特別地,設
為非循環群,
>2則對於1≤
≤
-1有
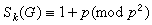 有限群
有限群(庫拉科夫定理)。又令
(
)表
階群
中
階循環子群的個數。設
是非循環群,
>2,則對於1<
<
有
(
)呏0(mod
)(米勒定理)。兩者以及其他的一些計數定理皆可用P.霍爾的計數原理來證明。在這方面華羅庚、段學復早在20世紀40年代就曾一起進行過一些工作。例如,設
>2,|
|=
,
為
中元素之階的最大數,且
≥2α+1,華羅庚於1945年證明了對於α+1≤m≤
-α有
(
)=
 有限群
有限群。段學復於1948年證明了對於 2α+1≤m≤
,
(
)與1,1+
,1+
+
、1+
+2
四者之一同餘mod
。所謂正則
群,是指具有如下性質的
群
:對於
的任意元素
、
恆可找到
個元素с
,с
,…,с
,使每個с
∈<
,
>┡=【<
,
>,<
,
>】即每個с
在由
、
生成的群之換位子群內,且有
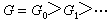 有限群
有限群,其中自然數
隨元素
、
決定。交換
群、階不超過
的
群以及冪零類小於
的
群,都是正則
群;換位子群為循環群而
為奇素數的
群、凡非單位元的階等於
的
群,也都是正則
群。正則
群在
群中有眾多例子。但非正則
群也是存在的,例如,
次對稱群
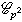 有限群
有限群中西洛
子群就是
階非正則
群。
擴張研究有限群的一個重要方法。設
、
B是已知的兩個群,如果作一群
,使得
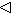 有限群
有限群,且商群
/
≌
B,那么群
稱為
B基於
的擴張。一般,
B基於
的擴張不是惟一的,例如,
與
B的直積
×
B是
B基於
的一個擴張,而
與
B的半直積也是
B基於
的擴張。所謂
與
半直積為
,是指
=
B,
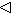 有限群
有限群,且
∩
B=1(即
B為
的補子群)。
與
B的半直積又稱為
的分離擴張。
B基於
的擴張為
與
B的半直積的一個充分條件是:
的階與
B的階互素。這就是著名的舒爾-扎森豪斯定理。當
B為循環群時,很容易決定擴張的構造。例如,m階循環群基於
階循環群的擴張,必為
=<
,
>,有定義關係
=1,
=
,
=
使滿足
呏1(mod
)及
(
-1)呏0(mod
)。因為有限群有合成群列
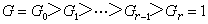 有限群
有限群,這裡,
/
是單群。因此,
是單群,且
是
/
基於
的擴張。若得知
的構造,則可藉助於擴張理論得知
的構造,從
的構造以及
是
/
基於
的擴張可知
的構造,如此繼續進行下去,則終究可得知
的構造。由此可見,研究單群與擴張理論是有限群研究的根本課題。
轉移研究有限群的一個重要方法。設
是有限群
的任一個子群,將
表為
的右陪集的並集,即
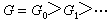 有限群
有限群,於是│
:
│=
。令
┡=【
,
】,並作商群
/
┡,且用
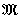 有限群
有限群表以
關於
┡的右陪集為元素的集合,若令
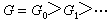 有限群
有限群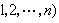 有限群
有限群,則知
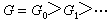 有限群
有限群的每一元素可惟一表為
=
,即惟一決定數碼
及交換群
/
┡的一個代表元素
,
∈
,因此,對
的每一元素
,有
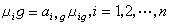 有限群
有限群,式中(1
,2
,…,
)為(1,2,…,
)的一個排列,且
∈
。作矩陣
=(
)使其第
行第
列交叉處的元素為
(
=1,2,…,
),而其他處的元素均為0。易證
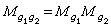 有限群
有限群。由此可知,映射
→
是
的一個同態映射,稱為
的單項表示。因
/
┡是交換群,故可引進行列式
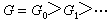 有限群
有限群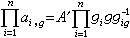 有限群
有限群,簡記為
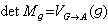 有限群
有限群。於是,映射
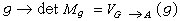 有限群
有限群也是
的同態映射,即
到
/
┡內的同態映射,稱為
到子群
的轉移。利用轉移方法可得出許多重要結果。例如,有限群
的西洛
子群
若包含於其正規化子的中心之內,即
 有限群
有限群,則有
=
,
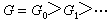 有限群
有限群,
∩
=1。這就是又一個著名的伯恩賽德定理。由此可知,階為合數的單群只有兩種可能:或為階被12整除的單群或為階被8整除的單群。
超可解群 它是介乎冪零群與可解群之間的一類有限群。所謂超可解群,是指有限群
有一個有限多個正規子群的遞降列
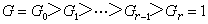 有限群
有限群使每個商群
/
為循環群。因此,超可解群是可解群的特例,又是冪零群的推廣。判斷有限群
為超可解群有許多等價的充分必要條件,其中常見的有:①
的每個極大子群的指數為素數;②
的主群列的商因子皆為素數階的循環群;③
的每一子群
(≤
)都有一切可能階的子群。
參考書目
W. Burnside,
, 2nd ed.,Cambridge Univ. Press, Cambridge, 1911.
D.Gorenstein,
, Harper and Row, New York, 1968.
B.Huppert,
,I,Springer-Verlag,Berlin, 1967.
相關連線
有限群論壇http://rulin.uu1001.com
