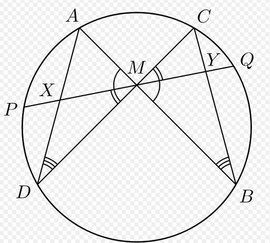
定義
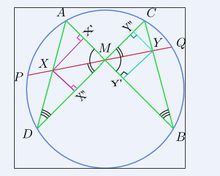蝴蝶定理的證明去掉中點的條件，結論變為一個一般關於有向線段的比例式，稱為“坎迪定理”， 不為中點時滿足:1/MY-1/MX=1/MQ-1/MP ,這對2，3均成立。
驗證
方法1
（霍納證法）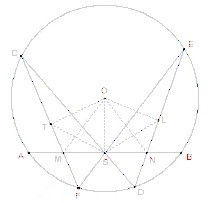
霍納證法連線ON，OM，OS，SL，ST，易明△ESD∽△CSF
∴ES/CS=ED/FC
根據垂徑定理得：LD=ED/2，FT=FC/2
∴ES/CS=EL/CT
又∵∠E=∠C
∴△ESL∽△CST
∴∠SLN=∠STM
∵S是AB的中點所以OS⊥AB
∴∠OSN=∠OLN=90°
取OM中點X，在Rt△MTO和△OSM中，TX=OX=MX=SX
∴O，S，N，L四點共圓，（一中同長）
同理，O，T，M，S四點共圓
∴∠STM=∠SOM，∠SLN=∠SON
∴∠SON=∠SOM
∵OS⊥AB
∴MS=NS
方法2
蝴蝶定理的證明從X向AM和DM作垂線，設垂足分別為X'和X''。類似地，從Y向BM和CM作垂線，設垂足分別為Y'和Y''。
（證明過程見圖片）
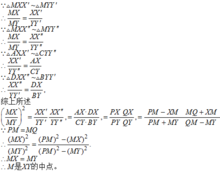證明方法二方法3
（對稱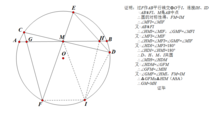法）
對稱證法（證明過程見圖片）
方法4
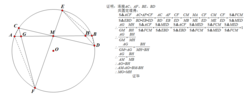面積法（證明過程見圖片）
方法5
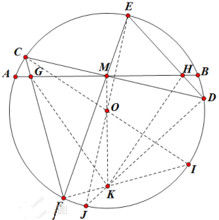帕斯卡證法連線CO、EO並延長分別交圓O於I、J，連線IF、DJ交於K，
連線GK、HK。由帕斯卡定理得：M、O、K共線
∵M為AB中點 ∴KM⊥AB∴∠GMK=∠HMK=90°
又∵CI、EJ為⊙O直徑 ∴∠GFK=∠HDK=90°
又∵∠GMK=∠HMK=90° ∴∠GMK+∠GFK=∠HMK+∠HDK=90°+90°=180°，
∴G、F、K、M共圓，H、D、K、M共圓 ∴∠GKM=∠GFM，∠MKH=∠MDH
又∵∠GFM=∠MDH ∴∠GKM=∠MKH 又∵∠GMK=∠HMK=90°
∴△GMK≡△HMK（ASA）∴GM=MH
定理推廣
該定理實際上是射影幾何中一個定理的特殊情況，有多種推廣：M，作為圓內弦是不必要的，可以移到圓外。
蝴蝶定理的圓外形式：
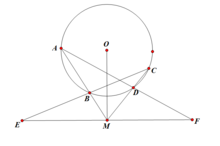圓外蝴蝶定理如圖，延長圓O中兩條弦AB與CD交於一點M，過PM做OM垂線，垂線與CB和AD的延長線交於E、F，則可得出ME=MF（證明方法可參考蝴蝶定理的證法2、3、4）
1.在橢圓中
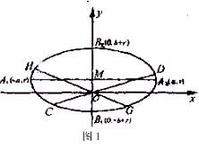橢圓中的蝴蝶定理如圖一，橢圓的長軸A、A與x軸平行，短軸BB在y軸上，
中心為M(o，r)（b>r>0）。
（I）寫出橢圓的方程，求橢圓的焦點坐標及離心率
（II）直線y=kx交橢圓於兩點C（x,y）,D(x，y)（y>0）；直線y=kx交橢圓於兩點G（x，y），H（x，y）（y>0）。求證：kxx/(x+x)=kxx/(x+x)
（III）對於（Ⅱ）中的C，D，G，H，設CH交X軸於點P，GD交X軸於點Q。
求證： | OP | = | OQ |。（證明過程不考慮CH或GD垂直於X軸的情形）
從x向AM和DM作垂線，設垂足分別為X'和X''。
類似地，從Y向BM和CM作垂線，設垂足分別為Y'和Y'
證明過程圖片設：k1x1x2/(x1+x2)=k2x3x4/(x3+
x4)為①式，兩邊同取倒數，得為
1/k1x2+1/k1x1=1/k2x4+1/k2x3 ①’
設：x1x4/(k1x1-k2x4)=-x2x3/(k1x2-k2x3)為 ②式，兩邊同取倒數，得k1/x4-k2/x1=k2/x2-k1/x3，移項得k2/x1+k2/x2=k1/x3+k1/x4 ②’
將①’兩邊同乘以k1·k2，即得
k2/x1+k2/x2=k1/x3+k1/x4
它與②’完全一樣。這裡利用兩式同時變形的方法可以較容易實現目的，有分析、有綜合，有思維，有運算。思路的選擇有賴於對式子特徵的觀察聯想。
縱觀這道題的題目特徵及解答過程，我們看到了用代數方程方法處理幾何問題的作用與威力。
2.在圓錐曲線中
通過射影幾何，我們可以非常容易的將蝴蝶定理推廣到普通的任意圓錐曲線（包括橢圓，雙曲線，拋物線，甚至退化到兩條相交直線的情況）。
圓錐曲線C上弦PQ的中點為M，過點M任作兩弦AB，CD，弦AD與BC分別交PQ於X，Y，則M為XY之中點。
而通過投影變換可以非常容易證明這個定理。
射影幾何裡面關於投影變換有一個重要結論，對於平面上任意兩個圓錐曲線C1,C2.任意指定C1內部一個點A1和C1上面一個點B1,另外任意指定C2內部一個點A2和C2上面一個點B2,存在一個唯一投影變換將曲線C1變換到C2而且A1變換到A2,B1變換到B2.
由此對於本題，我們可以通過投影變換將C1變換成一個圓M，而將弦PQ的中點M變換成這個圓的圓心。
在此變換以後，弦AB和CD都是圓M的直徑而且四邊形ACBD是圓M內接矩形，PQ也是一條直徑，有對稱性顯然得出投影變換後M為X,Y的中點。又因為變換前後M都是線段PQ的中點，我們可以得出在直線PQ上這個變換是仿射變換，所以變換前M也是XY的中點。
3.在平行四邊形中
在平行四邊形中，，M為對角線AB與CD中點。
4.坎迪定理
去掉中點的條件，結論變為一個一般關於向量的比例式，成為「坎迪定理」，這對2，3均成立
定理歷史
這個命題最早作為一個征解問題出現在公元1815年英國的一本雜誌《男士日記》（Gentleman's Diary）39-40頁（P39-40）上。有意思的是，直到1972年以前，人們的證明都並非初等，且十分繁瑣。
這篇文章登出的當年，英國一個自學成才的中學數學教師W.G.霍納（他發明了多項式方程近似根的霍納法）給出了第一個證明，完全是相等的；另一個證明由理察·泰勒（Richard Taylor）給出。
另外一種早期的證明由M.布蘭德（Mile Brand）1827年的一書中給出。最為簡潔的證法是射影幾何的證法，由英國的J·開世在"A Sequel to the First Six Books of the Elements of Euclid"給出，只有一句話，用的是線束的交比。
“蝴蝶定理”這個名稱最早出現在《美國數學月刊》1944年2月號，題目的圖形象一隻蝴蝶。
1981年，Crux雜誌刊登了K.薩蒂亞納拉亞納（Kesirajn Satyanarayana）用解析幾何的一種比較簡單的方法，利用直線束，二次曲線束。
定理意義
蝴蝶定理是古典歐式平面幾何的最精彩的結果之一。這個定理的證法不勝枚舉，至今仍然被數學熱愛者研究，在考試中時有出現各種變形。
相關讀物
關於“橢圓上的蝴蝶”，張景中院士在其獻給中學生的禮物一書《數學家的眼光》“巧思妙解”一節中有著精妙的論述，有興趣的讀者請參閱該書P54-59。
