定義
垂直於弦的直徑平分這條弦,並且平分弦所對的兩條弧。
逆定理:平分弦(不是直徑)的直徑垂直於弦,並且平分弦所對的兩條弧
證明
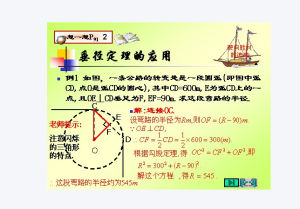
如圖,在⊙O中,DC為直徑,AB是弦,AB⊥DC於點E,AB、CD交於E,求證:AE=BE,弧AC=弧BC,弧AD=弧BD
證明:連OA、OB分別交於點A、點B.
 垂徑定理
垂徑定理∵OA、OB是⊙O的半徑
∴OA=OB
∴△OAB是等腰三角形
∵AB⊥DC
∴AE=BE,∠AOE=∠BOE(等腰三角形的三線合一性質)
∴弧AD=弧BD,∠AOC=∠BOC
∴弧AC=弧BC
推論
推論一:平分弦(不是直徑)的直徑垂直於這條弦,並且平分這條弦所對的兩段弧
推論二:弦的垂直平分線經過圓心,並且平分這條弦所對的弧
推論三:平分弦所對的一條弧的直徑垂直平分這條弦,並且平分這條弦所對的另一條弧
推論四:在同圓或者等圓中,兩條平行弦所夾的弧相等
(證明時的理論依據就是上面的五條定理)
但是在做不需要寫證明過程的題目中,可以用下面的方法進行判斷:
一條直線,在下列5條中只要具備其中任意兩條作為條件,就可以推出其他三條結論
1.平分弦所對的優弧
2.平分弦所對的劣弧
(前兩條合起來就是:平分弦所對的兩條弧)
3.平分弦(不是直徑)
4.垂直於弦
5.經過圓心
有關性質
知識點
圓、圓的對稱性、點和圓的位置關係、不在同一直線上的三點確定一個圓、三角形的外接圓、垂徑定理逆定理、圓心角、弧、弦、弦心距之間的關係、圓周角定理、圓內接四邊形的性質
大綱要求
1.正確理解和套用圓的點集定義,掌握點和圓的位置關係;
2.熟練地掌握確定一個圓的條件,即圓心、半徑;直徑;不在同一直線上三點。一個圓的圓心只確定圓的位置,而半徑也只能確定圓的大小,兩個條件確定一條直線,三個條件確定一個圓,過三角形的三個頂點的圓存在並且唯一;
3.熟練地掌握和靈活套用圓的有關性質:同(等)圓中半徑相等、直徑相等直徑是半徑的2倍;直徑是最大的弦;圓是軸對稱圖形,經過圓心的任一條直線都是對稱軸;圓是中心對稱圖形,圓心是對稱中心;圓具有鏇轉不變性;垂徑定理及其推論;圓心角、圓周角、弧、弦、弦心距之間的關係;
4.掌握和圓有關的角:圓心角、圓周角的定義及其度量;圓心角等於同(等)弧上的圓周角的2倍;同(等)弧上的圓周角相等;直徑(半圓)上的圓周角是直角;90°的圓周角所對的弦是直徑;
5.掌握圓內接四邊形的性質定理:它溝通了圓內外圖形的關係,並能套用它解決有關問題;
6.注意:
(1)垂徑定理及其推論是指:一條弦在
①過圓心
②垂直於另一條弦
③平分這另一條弦
④平分這另一條弦所對的劣弧
⑤平分這另一條弦所對的優弧的
五個條件中任意具有兩個條件,則必具有另外三個結論(當①③為條件時要對另一條弦增加它不是直徑的限制),條理性的記憶,不但簡化了對它實際代表的10條定理的記憶且便於解題時的靈活套用,垂徑定理提供了證明線段相等、角相等、垂直關係等的重要依據;
(2)有弦可作弦心距組成垂徑定理圖形;見到直徑要想到它所對的圓周角是直角,想垂徑定理;想到過它的端點若有切線,則與它垂直,反之,若有垂線則是切線,想到它被圓心所平分;
(3)見到四個點在圓上想到有4組相等的同弧所對的圓周角,要想到套用圓內接四邊形的性質。
常見題型
1.判斷基本概念、基本定理等的正誤,在中考題中常以選擇題、填空題的形式考查學生對基本概念和基本定理的正確理解。
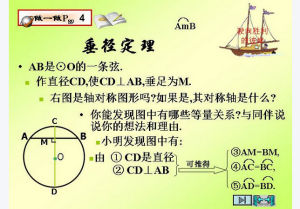
如:下列語句中,正確的有()
 垂徑定理
垂徑定理(A)相等的圓心角所對的弧相等(B)平分弦的直徑垂直於弦
(C)長度相等的兩條弧是等弧(D)弦過圓心的每一條直線都是圓的對稱軸
答案為D,
解析:
其中A和C都少了同圓的限定條件。如果是兩個半徑不同的圓內,即使是弧對應圓心角相等或弧的長度相等也不能得到弧相等。
B錯在弦可以是特殊弦:直徑。如果是直徑平分直徑,結論是直徑並不都相互垂直。
2.論證線段相等、三角形相似、角相等、弧相等及線段的倍分等。
此種結論的證明重點考查了全等三角形和相似三角形判定,垂徑定理及其推論、圓周角、圓心角的性質及切線的性質,弦切角等有關圓的基礎知識,常以解答題形式出現。
二,〖知識點〗
相交弦定理、切割線定理及其推論
〖大綱要求〗
1.正誤相交弦定理、切割線定理及其推論;
2.了解圓冪定理的內在聯繫;
3.熟練地套用定理解決有關問題;
4.注意(1)相交弦定理、切割線定理及其推論統稱為圓冪定理,圓冪定理是圓和相似三角形結合的產物。這幾個定理可統一記憶成一個定理:過圓內或圓外一點作圓的兩條割線,則這兩條割線被圓截出的兩弦被定點分(內分或外分)成兩線段長的積相等(至於切線可看作是兩條交點重合的割線)。使用時注意每條線段的兩個端點一個是公共點,另一個是與圓的交點;
(2)見圓中有兩條相交想到相交弦定理;見到切線與一條割線相交則想到切割線定理;若有兩條切線相交則想到切線長定理,並熟悉此時圖形中存在著一個以交點和圓心連線為對稱軸的對稱圖形。
考查重點與常見題型
證明等積式、等比式及混合等式等。此種結論的證明重點考查了相似三角形,切割線定理及其推論,相交弦定理及圓的一些知識。常見題型以中檔解答題為主,也有一些出現在選擇題或填空題中。

