介紹
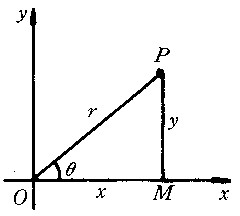三角學定義
研究平面三角形和球面三角形邊角關係的數學學科。三角學是以研究三角形的邊和角的關係為基礎，套用於測量為目的，同時也研究三角函式的性質及其套用的一門學科。
起源
三角學起源於古希臘。為了預報天體運行路線、計算日曆、航海等需要，古希臘人已研究球面三角形的邊角關係，掌握了球面三角形兩邊之和大於第三邊，球面三角形內角之和大於兩個直角，等邊對等角等定理。印度人和阿拉伯人對三角學也有研究和推進，但主要是套用在天文學方面。１５、１６世紀三角學的研究轉入平面三角，以達到測量上套用的目的。１６世紀法國數學家韋達系統地研究了平面三角。他出版了套用於三角形的數學定律的書。此後，平面三角從天文學中分離出來，成了一個獨立的分支。平面三角學的內容主要有三角函式、解三角形和三角方程。
三角測量在中國也很早出現，公元前一百多年的《周髀算經》就有較詳細的說明，例如它的首章記錄“周公曰，大哉言數，請問用矩之道。商高曰，平矩以正繩，偃矩以望高，復矩以測深，臥矩以知遠。”（商高說的矩就是今天工人用的兩邊互相垂直的曲尺，商高說的大意是將曲尺置於不同的位置可以測目標物的高度、深度與廣度）１世紀時的《九章算術》中有專門研究測量問題的篇章。
歷史
早期三角學不是一門獨立的學科，而是依附於天文學，是天文觀測結果推算的一種方法，因而最先發展起來的是球面三角學．希臘、印度、阿拉伯數學中都有三角學的內容，可大都是天文觀測的副產品．例如，古希臘門納勞斯（Ｍｅｎｅｌａｕｓ ｏｆ Ａｌｅｘａｎｄｒｉａ，公元100年左右）著《球面學》，提出了三角學的基礎問題和基本概念，特別是提出了球面三角學的門納勞斯定理；50年後，另一個古希臘學者托勒密（Ｐｔｏｌｅｍｙ）著《天文學大成》，初步發展了三角學．而在公元４９９年，印度數學家阿耶波多（ｒｙａｂｈａｔａ Ｉ）也表述出古代印度的三角學思想；其後的瓦拉哈米希拉（Ｖａｒａｈａｍｉｈｉｒａ，約５０５～５８７）最早引入正弦概念，並給出最早的正弦表；公元１０世紀的一些阿拉伯學者進一步探討了三角學．當然，所有這些工作都是天文學研究的組成部分．直到納西爾丁（Ｎａｓｉｒ ｅｄ－Ｄｉｎ ａｌ Ｔｕｓｉ，１２０１～１２７４）的《橫截線原理書》才開始使三角學脫離天文學，成為純粹數學的一個獨立分支．而在歐洲，最早將三角學從天文學獨立出來的數學家是德國人雷格蒙塔努斯（Ｊ Ｒｅｇｉｏｍｏｎｔａｎｕｓ，１４３６～１４７６）。
雷格蒙塔努斯的主要著作是１４６４年完成的《論各種三角形》。這是歐洲第一部獨立於天文學的三角學著作。全書共５卷，前２卷論述平面三角學，後３卷討論球面三角學，是歐洲傳播三角學的源泉。雷格蒙塔努斯還較早地製成了一些三角函式表。
雷格蒙塔努斯的工作為三角學在平面和球面幾何中的套用建立了牢固的基礎．他去世以後，其著作手稿在學者中廣為傳閱，並最終出版，對 16 世紀的數學家產生了相當大的影響，也對哥白尼等一批天文學家產生了直接或間接的影響．。
三角學一詞的英文是ｔｒｉｇｏｎｏｍｅｔｒｙ，來自拉丁文ｔｕｉｇｏｎｏｍｅｔｕｉａ．最先使用該詞的是文藝復興時期的德國數學家皮蒂斯楚斯（Ｂ．Ｐｉｔｉｓｃｕｓ，１５６１～１６１３），他在１５９５年出版的《三角學：解三角形的簡明處理》中創造這個詞．其構成法是由三角形（ｔｕｉａｎｇｕｌｕｍ）和測量（ｍｅｔｕｉｃｕｓ）兩字湊合而成．要測量計算離不開三角函式表和三角學公式，它們是作為三角學的主要內容而發展的．
１６世紀三角函式表的製作首推奧地利數學家雷蒂庫斯（Ｇ．Ｊ．Ｒｈｅｔｕｃｕ ｓ，１５１４～１５７４）。他１５３６年畢業於滕貝格大學，留校講授算術和幾何。１５３９ 年赴波蘭跟隨著名天文學家哥白尼學習天文學，１５４２年受聘為萊比錫大學數學教授．雷蒂庫斯首次編制出全部６種三角函式的數表，包括第一張詳盡的正切表和第一張印刷的正割表。
１７世紀初對數發明後大大簡化了三角函式的計算，製作三角函式表已不再是很難的事，人們的注意力轉向了三角學的理論研究．不過三角函式表的套用卻一直占據重要地位，在科學研究與生產生活中發揮著不可替代的作用．
三角公式是三角形的邊與角、邊與邊或角與角之間的關係式．三角函式的定義已體現了一定的關係，一些簡單的關係式在古希臘人以及後來的阿拉伯人中已有研究．
文藝復興後期，法國數學家韋達（Ｆ Ｖｉｅｔａ）成為三角公式的集大成者．他的《套用於三角形的數學定律》（１５７９）是較早系統論述平面和球面三角學的專著之一．其中第一部分列出６種三角函式表，有些以分和度為間隔。給出精確到５位和１０位小數的三角函式值，還附有與三角值有關的乘法表、商表等。第二部分給出造表的方法，解釋了三角形中諸三角線量值關係的運算公式．除匯總前人的成果外，還補充了自己發現的新公式．如正切定律、和差化積公式等等．他將這些公式列在一個總表中，使得任意給出某些已知量後，可以從表中得出未知量的值．該書以直角三角形為基礎。對斜三角形，韋達仿效古人的方法化為直角三角形來解決．對球面直角三角形，給出計算的完整公式及其記憶法則，如餘弦定理，１５９１年韋達又得到多倍角關係式，１５９３ 年又用三角方法推導出餘弦定理。
１７２２年英國數學家棣莫弗（Ａ Ｄｅ Ｍｅｉｖｅｒ）得到以他的名字命名的三角學定理
（ｃｏｓθ±ｉｓｉｎθ）ｎ＝ｃｏｓｎθ＋ｉｓｉｎｎθ，
並證明了ｎ是正有理數時公式成立；１７４８年歐拉（Ｌ Ｅｕｌｅｒ）證明了ｎ是任意實數時公式也成立，他還給出另一個著名公式
ｅｉθ＝ｃｏｓθ＋ｉｓｉｎθ，
對三角學的發展起到了重要的推動作用．
近代三角學是從歐拉的《無窮分析引論》開始的．他定義了單位圓，並以函式線與半徑的比值定義三角函式，他還創用小寫拉丁字母ａ、ｂ、ｃ表示三角形三條邊，大寫拉丁字母Ａ、Ｂ、Ｃ表示三角形三個角，從而簡化了三角公式．使三角學從研究三角形 解法進一步轉化為研究三角函式及其套用，成為一個比較完整的數學分支學科．而由於上述諸人及 19 世紀許多數學家的努力，形成了現代的三角函式符號和三角學的完整的理論.
特點與運用
早期三角學不是一門獨立的學科，而是依附於天文學，是天文觀測結果推算的一種方法，因而最先發展起來的是球面三角學．希臘、印度、阿拉伯數學中都有三角學的內容，可大都是天文觀測的副產品．直到13世紀中亞數學家納速拉丁在總結前人成就的基礎上，著成《完全四邊形》一書，才把三角學從天文學中分離出來．15世紀，德國的雷格蒙塔努斯（J·Regiomontanus，1436—1476）的《論三角》一書的出版，才標誌古代三角學正式成為獨立的學科．這本書中不僅有很精密的正弦表、餘弦表等，而且給出了現代三角學的雛形．
16世紀法國數學家韋達（F·Viete，1540—1603）則更進一步將三角學系統化，在他對三角研究的第一本著作《套用於三角形的數學法則》中，就有解直角三角形、斜三角形等的詳述．18世紀瑞士數學家歐拉（L·Euler，1707—1783），他首先研究了三角函式．這使三角學從原先靜態研究三角形的解法中解脫出來，成為反映現實世界中某些運動和變化的一門具有現代數學特徵的學科．歐拉不僅用直角坐標來定義三角函式，徹底解決了三角函式在四個象限中的符號問題，同時引進直角坐標系，在代數與幾何之間架起了一座橋樑，通過數形結合，為數學的學習與研究提供了重要的思想方法．著名的歐拉公式，把原來人們認為互不相關的三角函式和指數函式聯繫起來了，為三角學增添了新的活力．
因此三角學是源於測量實踐，其後經過了漫長時間的孕育，眾多中外數學家的不斷努力，才逐漸豐富，演變發展成為現在的三角學。
計算方法
三角學中的三角函式有6個，是用幾何方法定義的。在直角坐標系中，設以射線Ox為始邊，OP為終邊的角為θ，P點的坐標為(x，y)，｜OP｜＝r，這時6個比由θ的大小確定，都是θ的函式，稱它們為角θ的三角函式，分別記作並分別稱為角θ的正弦、餘弦、正切、餘切、正割、餘割。tg，ctg，csc也分別記作tan，cot，cosec。同角三角函式間有3組運算關係，即
三角函式都是周期函式，以2π為周期。
三角函式的基本恆等式有和角公式：
sin(a＋β)＝sinαcosβ＋cosαsinβ
cos(a＋β)＝cosαcosβ－sinαsinβ
由這兩個公式可以導出差角公式、倍角公式、半角公式、和差化積與積化和差等公式。
解三角形是已知三角形的某些元素（邊和角）時求其餘未知元素。設三角形的三個角為A，B，C，它們所對的邊分別為a，b，c，則有
正弦定理：a/sinA=b/sinB=c/sinC=2R（2R在同一個三角形中是恆量，是此三角形外接圓的半徑的兩倍）
餘弦定理：a2＝b2＋c2－2bccosA這兩個定理是解三角形的主要依據。
三角方程一般指含有某些三角函式的方程，並且三角函式的自變數中含有未知數。由於每個三角函式都是周期函式，所以任何一個三角方程只要有解，就有無窮多個解。
三角測量
三角測量是指在導航，測量及土木工程中精確測量距離和角度的技術，主要用於為船隻或飛機定位。它的原理是：如果已知三角形的一邊及兩角，則其餘的兩邊一角可用平面三角學的方法計算出來。在西方，古希臘著名的數學家畢達哥拉斯首次證明了有關直角三角形的“畢達哥拉斯定理”，即中國的“勾股定理”，對幾何學研究及其套用做出了巨大貢獻.
正文
以研究平面三角形和球面三角形的邊和角的關係為基礎，達到測量上的套用為目的的一門學科。同時還研究三角函式的性質以及它的套用。
簡史 古代埃及人已有三角學知識，三角法主要是適應測量上的需要而產生的。例如，建築金字塔，整理尼羅河泛濫後的耕地，以及通商航海，觀測天象的需要。希臘的自然哲學家泰勒斯的相似理論，可以認為是三角學的萌芽，但歷史上都認為希臘的天文學家喜帕恰斯是三角學的創始者。他著有三角學12卷，並作成弦表。
印度人從天文、測量的角度，曾研究過三角學，在公元6世紀,有阿耶波多第一也曾作出正弦表。中國唐代，瞿曇悉旺達在他所編的《開元占經》中曾介紹了印度的正弦表。
德國的J.雷格蒙塔努斯曾研究過天文學與三角學。在他的《論三角》一書中，有仿印度人的正弦表作成的非常精密的正、餘弦表。他對天文、航海、測量方面都有很大的貢獻。
16世紀法國著名數學家F.韋達的《套用於三角形的數學法則》，是他對三角法研究的第一本書，其中包括他對解直角三角形、斜三角形的一些貢獻，例如有正切定理：
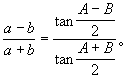
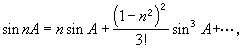
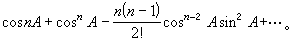
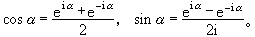
三角函式 在直角坐標系中,以原點O為頂點，射線Ox為始邊，Op為終邊的角為θ,設點p的坐標為(x,y),距離｜Op｜=r,這時6個比
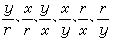由角θ的大小確定，都是θ的函式，稱它們為角θ 的三角函式（見圖1
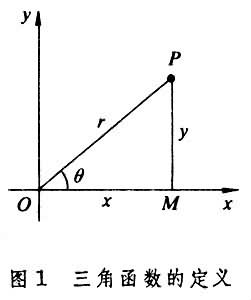），分別記以下面的符號：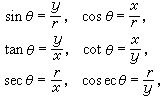 
另外在中國古書中，又把1-cosθ、1-sinθ分別叫做正矢、余矢，用下面符號表示：
,
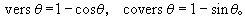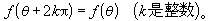
如圖2
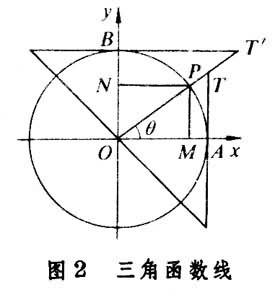以O為圓心,以1為半徑作單位圓。設它與x軸、y軸交於點A、B,∠AOp的終邊與圓的切線AT、BT┡分別交於T、T┡，pM⊥Ox，pN⊥Oy。這時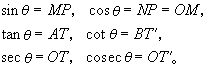 
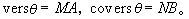
利用三角函式線，可以畫出三角函式的曲線。例如，標準正弦曲線y＝sinx（如圖3
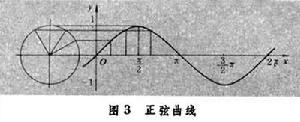）。 三角函式的基本公式有和角公式：
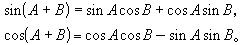
如果θ表示弧度，對於θ的任意值，sinθ、cosθ可用下面的無窮級數表示：
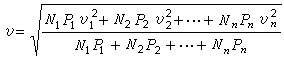
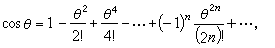
三角形的解法 設平面三角形的三個角為A、B、C，它們的對邊分別為α、b)、с，則有
正弦定理：
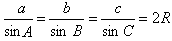（R 為外接圓半徑）； 餘弦定理：
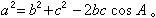
又設球面三角形的三個角為A、B、C,它們的對邊分別為α、β、у，則有
正弦定理：
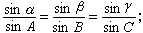
餘弦定理：
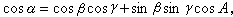
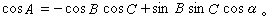
利用上述定理以及其他一些定理，可在已知三角形的某些元素（邊或角）時求出其他未知元素。
反三角函式 其定義如表所示：
三角學適合於方程的一個未知數的實數值（可以理解為角的弧度數）叫做三角方程的一個解；適合於方程的未知數的實數值的集合叫做三角方程的通解。
形如sinx=α的方程叫做最簡三角方程。它們的解分別是：
① sinx＝α
當｜α｜>1時無解。當α=1時通解為
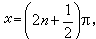
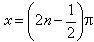。當｜α｜<1時，通解為x＝nπ+(-1)narcsin α（n為整數）。 ② cosx＝α
當｜α｜>1時無解。當α=1時通解為x=2nπ，當α=-1時通解為 x＝(2n+1)π。當｜α｜<1 時通解為x＝2nπ±arccosα（n為整數）。
③ tan x＝α
通解為nπ+arctanα （n為整數）。
④ cot x＝α
通解為nπ+arccotα （n為整數）。
一些特殊形式的三角方程可有精確解法。例如，形如ƒ（sinx,cosx,tanx,cotx）=0的方程，這裡ƒ是有理函式，可用萬能公式，令
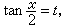然後以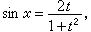
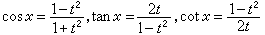代入原方程,即可得到關於t的有理方程。用這個方法,可以求出除了形如x＝(2n+1)π以外的方程的所有解。不能用精確解法來解的三角方程，可以用近似方法求解。