證明
方法一
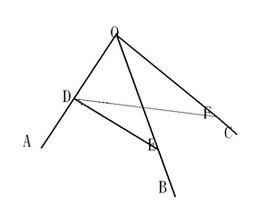
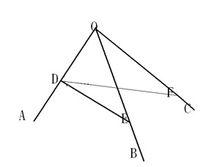
三面角餘弦定理在OA上取一點D，過D作OD的垂線DE、DF分別交OB、OC於E與F。接著使用向量證明。
考慮有向線段 OD、 OE、 OF、 DE、 DF。易知：
cos∠OA= DE· DF/(DE*DF)
sin∠AOB=DE/OE
sin∠AOC=DF/OF
cos∠AOB=OD/OE
cos∠AOC=OD/OF
cos∠BOC= OE· OF/(OE*OF)；
則實際是要證明：
DE· DF/(DE*DF)*DE/OE*DF/OF+OD/OE*OD/OF= OE· OF/(OE*OF)
整理得( DE· DF+OD²)/(OE*OF)= OE· OF/(OE*OF)
即是要證明OD²+ DE· DF= OE· OF；
顯然， OE· OF=( OD+ DE)·( OD+ DF)=OD²+ OD· DE+ OD· DF+ DE· DF，
注意到 OD· DE= OD· DF=0，即可證明原式。
方法二
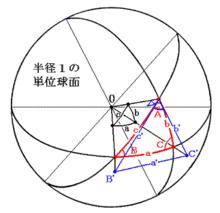
三面角餘弦定理將三面角O-ABC放入單位球中，並設三面角與球面的交點分別為A、B、C。過A作球面的切平面，射線OB、OC與切平面交點為B'、C‘。則：
∠OA=∠B'AC'=A，AB'=tan∠AOB=tanc，AC'=tan∠AOC=tanb，OB'=1/cos∠AOB=1/cosc，OC'=1/cos∠AOC=1/cosb
在△AB'C'中，由余弦定理得
B'C'²=tan²c+tan²b-2tanc*tanb*cosA
在△OB'C'中，由余弦定理得
B'C'²=1/cos²c+1/cosb-2cos∠BOC/(cosc*cosb)
∴sin²c/cos²c+sin²b/cos²b-2sinc*sinb*cosA/(cosc*cosb)
=1/cos²c+1/cos²b-2cos∠BOC/(cosc*cosb)
兩邊乘以cos²c*cos²b得
sin²c*cos²b+sin²b*cos²c-2sinc*cosc*sinb*cosb*cosA
=cos²b+cos²c-2cosb*cosc*cos∠BOC
移項，整理得
cos²b(1-sin²c)+cos²c(1-sin²b)-2cosb*cosc*cos∠BOC=-2sinc*cosc*sinb*cosb*cosA
化簡得cos∠BOC=cosb*cosc+sinb*sinc*cosA
也就是cos∠BOC=cos∠AOBcos∠AOC+sin∠AOBsin∠AOCcos∠OA
三面角餘弦定理第二形式
第二形式
在三面角O-ABC中，設二面角B-OA-C為∠OA，則有：
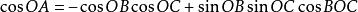三面角餘弦定理證明
將三面角O-ABC的頂點與單位球的球心重合，並設三邊與球面分別交於A、B、C。根據球面三角形的定義，在球面△ABC中，∠AOB=c，∠BOC=a，∠AOC=b；∠OA=A，∠OB=B，∠OC=C。則餘弦定理的第一形式可化為：
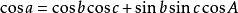三面角餘弦定理餘弦定理的第二形式可化為：
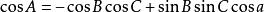三面角餘弦定理由於球面三角形與其極對稱三角形之間存在定量的邊角關係，因此不妨設球面△ABC的極對稱三角形為△A'B'C'，則在△A'B'C'中，由余弦定理的第一形式得
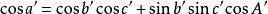三面角餘弦定理∵a'=π-A，b'=π-B，c'=π-C，A'=π-a
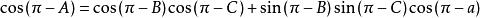三面角餘弦定理∴上式可化為
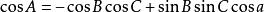三面角餘弦定理即
證明完畢
全向量證明
三面角餘弦定理的全向量證明