楊輝三角的性質
1、每行數字左右對稱,由1開始逐漸變大,然後變小,回到1。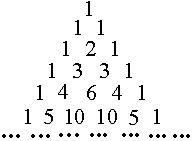 楊輝三角
楊輝三角2、第n行的數字個數為n個。
3、第n行數字和為2^(n-1)。
4、每個數字等於上一行的左右兩個數字之和。可用此性質寫出整個帕斯卡三角形。
5、將第2n+1行第1個數,跟第2n+2行第3個數、第2n+3行第5個數……連成一線,這些數的和是第2n個斐波那契數。將第2n行第2個數,跟第2n+1行第4個數、第2n+2行第6個數……這些數之和是第2n-1個斐波那契數。
6、第n行的第1個數為1,第二個數為1×(n-1),第三個數為1×(n-1)×(n-2)/2,第四個數為1×(n-1)×(n-2)/2×(n-3)/3…依此類推。
7.兩個未知數和的n次方運算後的各項係數依次為楊輝三角的第n行。
楊輝三角的實現
namespace楊輝三角{
///
///Class1的摘要說明。
///
class Class1{
///
///應用程式的主入口點。
///
[STAThread]
staticvoidMain(string[]args)
{
Console.WriteLine("inputtherownum:");
intr=int.Parse(Console.ReadLine());
int[,]a=newint[r+1,r+1];
inti=0;intj=0;
for(;i {
j=0;
for(;j<=i;j++)
{
if(j==0||j==i)
else
{
a[i,j]=a[i-1,j-1]+a[i-1,j];
}
Console.Write("{0}\t",a[i,j]);
}
Console.WriteLine();
}
Console.Read();
}
}
}

