三角形的基本定義
由不在同一直線上的三條線段首尾順次連線所組成的{封閉圖形}叫做三角形。三角形的內角和為180度。由{平面}上的三條直線所圍成的圖形，叫｛平面三角形｝；由球面上（凹面；凸面）的三條弧線所圍成的圖形，叫{球面三角形}，也叫做｛三邊形｝
三角形分類
按角度分
a.{銳角三角形}：三個角都小於90度 。（其並不是只有一個銳角的三角形，而是三個角都為銳角，比如｛等邊三角形“也是銳角分別為60度的{三角形}。 並且其3條邊上的3條‘高’交於一點。
b.直角三角形（簡稱 ‘ Rt 三角形 ’）：
（1）直角三角形兩個銳角‘互余’（‘其之和為90度’之意）；
（2）直角三角形斜邊上的中線等於斜邊的一半；
（3）在直角三角形中，如果有一個銳角等於30°，那么它所對的直角邊等於斜邊的一半.；
（4）在直角三角形中，如果有一條直角邊等於斜邊的一半，那么這條直角邊所對的銳角等於30°（和⑶相反）；
（5）在直角三角形中，兩條直角邊a、b的平方和等於斜邊c的平方，即a^2＋b^2=c^2（勾股定理）；
（6）斜邊上的中線是外接圓半徑；
（7）有一個角是90度的三角形，夾90度的兩邊稱為“直角邊”，直角的對邊稱為“斜邊”。 (非直角三角形也稱斜三角形，包括銳角三角形、鈍角三角形)。
（8）在直角三角形中，斜邊的長度是直角對應的兩條直角邊的2^1/2倍。
（9）直角三角形的兩條高是那兩條直角邊。
c.鈍角三角形：有一個角為鈍角的三角形 。鈍角三角形有兩條高在鈍角三角形的外面,鈍角為大於90°且小於180°，並有兩條高不在三角形裡面。
d.正三角形：三個角度數相等（即三角都為60度），三條邊也相等，也稱等邊三角形。
按邊長分
a.等腰三角形：兩條邊相等的三角形。又可分為三條邊都相等的等腰三角形，即等邊三角形，和只有兩條邊相等的等腰三角形。普通等腰三角形中，兩條相等的邊稱為“腰”，第三邊叫做“底邊”，腰對應的角（稱為底角）也是相等的。
b.不等邊三角形：三條邊均不相等的三角形（此解釋有誤，因為等腰三角形也不是等邊三角形，應改為：三條變不均相等的三角形。）。
特殊三角形
面積為零的三角形；退化三角形（‘退化三角形’，按照狹義的三角形定義，其實已經不屬於三角形。例如一個內角變化為180度就成為一條線段，但是可以證明“兩點之間直線最短”公理）
周長公式
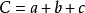（三角形周長Ｃ）若一個三角形的三邊分別為a、b、c，則周長C為
面積公式
1、面積
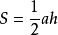三角形（面積=底×高÷2。其中，a是三角形的底，h是底所對應的高）注釋：三邊均可為底，應理解為：三邊與之對應的高的積的一半是三角形的面積。這是面積法求線段長度的基礎。
2、
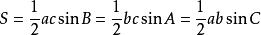（三角形面積）（其中，三個角為∠A，∠B，∠C，對邊分別為a，b，c。參見三角函式）
3、
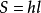三角形( ‘l’為高所在的邊的中位線）
4
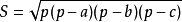（三角形面積）（海倫公式），其中
5
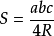三角形（其中，R是外接圓半徑）
6 （其中，r是內切圓半徑）
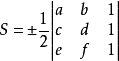（三角形面積）7 在平面直角坐標系內，A（a，b），B（c，d），C（e，f）構成之三角形面積為
。
A，B，C三點最好按逆時針順序從右上角開始取，因為這樣取得出的結果一般都為正值，如果不按這個規則取，可能會得到負值，但只要取絕對值就可以了，不會影響三角形面積的大小。
8
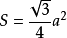三角形（正三角形面積公式，a是三角形的邊長）
9
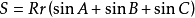三角形(其中，R是外接圓半徑；r是內切圓半徑）
10
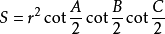（三角形面積）“四線”
１、中線
連線某一個三角形的‘一個頂點及頂點相對應的對邊的中點’得到的線段，叫做｛三角形的中線｝（median）。其有３條。
２、高
從一個頂點向它的對邊所在的直線畫｛垂線｝，頂點和垂足之間的｛線段｝的長，叫做｛三角形的高｝（altitude）。其有３條。
３、三角形的角平分線
在三角形中，其某一個內角的平分線的頂點，與此｛被分的角｝的頂點重合，在角的兩條邊中間， 是一條｛射線｝；此上面的實用的點，分別到兩條邊的距離相等；叫做｛角平分線｝【另外，數學也有{非三角形的兩條線組成的角｝的角平分線（bisector of angle）原理一樣。其有３條。
４、中位線
三角形的三邊中，任意兩邊的中點，的連線叫｛中位線｝。它平行於第三邊，並且等於第三邊的一半。[切記，中位線沒有逆定理。]
邊、角關係
三角函式，給出了直角三角形中邊和角的關係規律，可用來解‘三角形題’；
三角函式，是數學中屬於初等函式中，超越函式的一類。（請參考相關詞條）。
特殊點、線
‘五心、四圓、三點、一線’：這些都是三角形的全部特殊點，以及基於這些特殊點的相關幾何圖形。“五心”指重心、垂心、內心、外心和旁心；“四圓”指，內切圓、外接圓、旁切圓和歐拉圓；“三點”指，勒莫恩點、奈格爾點和歐拉點；“一線”即｛歐拉線｝。
‘五心’的距離：
OH²=9R²–(a²+b²+c²),
OG²=R²–(a²+b²+c²)/9,
OI²=R²–abc/(a+b+c)=R²–2Rr
GH²=4OG²
GI²=(p²+5r²–16Rr)/9,
HI²=4R²-p²+3r²+4Rr=4R²+2r²-(a²+b²+c²)/2,
其中，R是外接圓半徑；r是內切圓半徑。
三角形的穩定性
在所有平面多邊形中，唯三角形具穩定性。（是力學現象，三角形構件不容易被外力改變原來的形狀，例如‘鐵塔’由許多三角形構成特別堅固）
證明
任取三角形兩條邊，則兩條邊的非公共端點被第三條長度固定的邊連線：
∵第三條邊不可伸縮或彎折
∴兩端點距離固定
∴這兩條邊的夾角被固定而不變
∵這兩條邊是任取的
∴三角形的三個任意角都得到固定，進而將三角形固定
∴三角形有力學穩定性（證畢）
-------------
證明“n邊形（n≥4）沒有穩定性”
艾菲爾鐵塔任取n邊形（n≥4）兩條相鄰邊，則兩條邊的非公共端點被不止一條邊相連線：
∴角的兩端點的距離不固定，
∴這兩邊的夾角不固定，
∴n邊形（n≥4）每個角都不固定
∴n邊形（n≥4）沒有穩定性
（證畢）
作用
三角形的穩定性使其不像四邊形那樣易於變形，有著穩固、堅定、耐壓不容易變形的特點。三角形的結構在工程上有
金字塔著廣泛的套用。許多建築都是三角形的結構，如：艾菲爾鐵塔，埃及金字塔等等。
有關三角形的定理
中位線定理
中線定理
三角形內角和定理
三邊關係定理
勾股定理
射影定理
正弦定理
餘弦定理
梅涅勞斯定理
塞瓦定理
莫利定理
共角定理
重心定理
內心定理
旁心定理
歐拉線定理
費爾巴哈定理
拿破崙定理
相關定理：
重心定理
三角形的三條中線交於一點，這點到頂點的距離是它到對邊中點距離的2倍．
上述交點叫做三角形的重心.
外心定理
三角形的三邊的垂直平分線交於一點．
這點叫做三角形的外心.
垂心定理
三角形的三條高交於一點．
這點叫做三角形的垂心.
內心定理
三角形的三內角平分線交於一點．
這點叫做三角形的內心.
旁心定理
三角形一內角平分線和另外兩頂點處的外角平分線交於一點．
這點叫做三角形的旁心．三角形有三個旁心．
三角形的重心、外心、垂心、內心、旁心稱為三角形的五心．
它們都是三角形的重要相關點．
中位線定理
三角形的中位線平行於第三邊且等於第三邊的一半．
三邊關係定理
三角形任意兩邊之和大於第三邊，任意兩邊之差小於第三邊．
勾股定理
在Rt三角形ABC中，A≤90度，則
AB·AB+AC·AC=BC·BC
A〉90度，則
AB·AB+AC·AC>BC·BC
梅涅勞斯定理
梅涅勞斯（Menelaus）定理是由古希臘數學家梅涅勞斯首先證明的。它指出：如果一條直線與△ABC的三邊AB、BC、CA或其延長線交於F、D、E點，那么(AF/FB)×(BD/DC)×(CE/EA)=1。
證明：
過點A作AG∥BC交DF的延長線於G,
則AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得：AF/FB×BD/DC×CE/EA=AG/BD×BD/DC×DC/AG=1
它的逆定理也成立：若有三點F、D、E分別在的邊AB、BC、CA或其延長線上，且滿足(AF/FB)×(BD/DC)×(CE/EA)=1，則F、D、E三點共線。利用這個逆定理，可以判斷三點共線。
塞瓦定理
設O是△ABC內任意一點，AO、BO、CO分別交對邊於D、E、F，則 BD/DC*CE/EA*AF/FB=1
證明：
（Ⅰ）本題可利用梅涅勞斯定理證明：
∵△ADC被直線BOE所截，
∴ CB/BD*DO/OA*AE/EC=1 ①
而由△ABD被直線COF所截，∴ BC/CD*DO/OA*AF/BF=1②
②÷①:即得：BD/DC*CE/EA*AF/FB=1
（Ⅱ）也可以利用面積關係證明
∵BD/DC=S△ABD/S△ACD=S△BOD/S△COD=(S△ABD-S△BOD)/(S△ACD-S△COD)=S△AOB/S△AOC ③
同理 CE/EA=S△BOC/ S△AOB ④ AF/FB=S△AOC/S△BOC ⑤
③×④×⑤得BD/DC*CE/EA*AF/FB=1
利用塞瓦定理證明三角形三條高線必交於一點:
設三邊AB、BC、AC的垂足分別為D、E、F，
根據塞瓦定理逆定理，因為(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA）/[(CD*ctgB）]*[(AE*ctgB)/(AE*ctgC)]*[(BF*ctgC)/
[(AE*ctgB)]=1，所以三條高CD、AE、BF交於一點。
將三角形的三個內角三等分，靠近某邊的兩條三分角線相交得到一個交點，則這樣的三個交點可以構成一個正三角形。這個三角形常被稱作莫利正三角形。
