定理概述
 三正弦定理
三正弦定理 三正弦定理
三正弦定理 三正弦定理
三正弦定理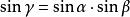 三正弦定理
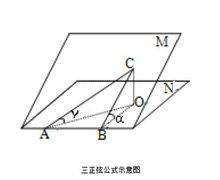
三正弦定理設二面角M-AB-N的度數為 ,在平面M上有一條射線AC,它和棱AB所成角為,和平面N所成的角為,則(如圖)。
(註明:摺疊角公式(又名:三餘弦定理)以及三正弦定理的套用為立體幾何的解題帶來了許多方便。)
若已知二面角其中一個半平面內某直線與二面角的棱所成的角,以及該直線與另一半平面所成的角,則可以求該二面角的正弦值。
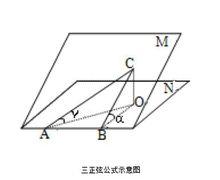 三正弦定理示意圖
三正弦定理示意圖定理證明
如上圖,過C作CO⊥平面N於點O,過O作直線OB⊥二面角的棱於點B,連OA,CB,則易知△CAO,△CBO,△ABC均為直角三角形.
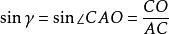 三正弦定理
三正弦定理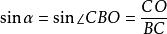 三正弦定理
三正弦定理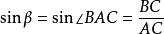 三正弦定理
三正弦定理於是,,,。
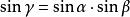 三正弦定理
三正弦定理由此容易推得 。
定理套用
如果將三正弦定理和三餘弦定理聯合起來,用於解答立體幾何綜合題,你會發現出乎意料地簡單,甚至不用作任何輔助線!
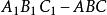 三正弦定理
三正弦定理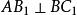 三正弦定理
三正弦定理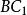 三正弦定理
三正弦定理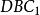 三正弦定理
三正弦定理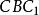 三正弦定理
三正弦定理例1 如圖,已知是正三稜柱,D是AC中點,若,求以為棱,與為面的二面角的度數(1994年全國高考理科數學23題)。
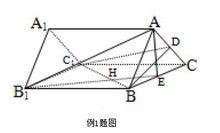 三正弦定理套用之例1題圖
三正弦定理套用之例1題圖 三正弦定理套用之例1解答
三正弦定理套用之例1解答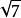 三正弦定理
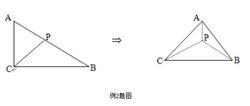
三正弦定理例2 已知Rt△ABC的兩直角邊AC=2,BC=3.P為斜邊AB上一點,現沿CP將此直角三角形折成直二面角A-CP-B(如下圖),當AB=時,求二面角P-AC-B大小(上海市1986年高考試題,難度係數0.28)。
 三正弦定理套用之例2題圖
三正弦定理套用之例2題圖 三正弦定理套用之例2解答
三正弦定理套用之例2解答參見
三餘弦定理