三面角正弦定理

三面角正弦定理是一個數學定理。是立體幾何的基本概念之一，是組成多面體的重要元素。與平面幾何中有關三角形的正、餘弦定理類似，有關三面角的正、餘弦定理是解三面角的重要依據。

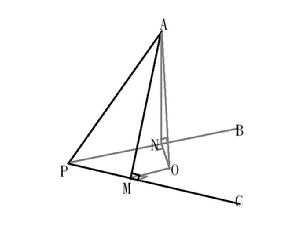
表述：

設三面角∠P-ABC的三個面角∠BPC，∠CPA，∠APB所對的二面角依次為∠PA，∠PB，∠PC，則
Sin∠PA／Sin∠BPC=Sin∠PB／Sin∠CPA=Sin∠PC/Sin∠APB。

證明：

過A做OA⊥平面BPC於O。過O分別做OM⊥BP於M與ON⊥PC於N。連結AM、AN。
顯然，∠PB=∠AMO，Sin∠PB=AO／AM；∠PC=∠ANO，Sin∠PC=AO／AN。
另外，Sin∠CPA=AN／ＡＰ，Sin∠APB=ＡＭ／ＡＰ。
則Sin∠PB／Sin∠CPA＝ＡＯ×ＡＰ／（ＡＭ×ＡＮ）＝Sin∠PC/Sin∠APB。
同理可證Sin∠PA／Sin∠BPC=Sin∠PB／Sin∠CPA。即可得證三面角正弦定理。