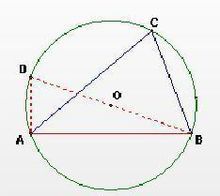
定義
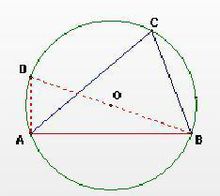 正弦公式
正弦公式Sine Law
正弦公式,即為正弦定理
在一個三角形中,各邊和它所對角的正弦的比相等。
即a/sinA=b/sinB=c/sinC=2R(2R在同一個三角形中是恆量,是此三角形外接圓的半徑的兩倍)
擴展
一.三角形面積公式:
設P=(a+b+c)/2
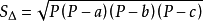 正弦公式
正弦公式解釋:假設有一個三角形,邊長分別為a、b、c,三角形的面積S可由以下公式求得:
S=根號下[p(p-a)(p-b)(p-c)]
而公式里的p為半周長:
p=(a+b+c)/2
2. S△ABC=(ab/2)·sinC=(bc/2)·sinA=(ac/2)·sinB=abc/(4R)[R為外接圓半徑]
3.S△ABC=ah/2
(1) a=2RsinA, b=2RsinB, c=2RsinC;
(2) sinA : sinB : sinC = a : b : c;
(條件同上)
在一個三角形中,各邊與其所對角的正弦的比相等,且該比值都等於該三角形外接圓的直徑已知三角形是確定的,利用正弦定理解三角形時,其解似的唯一的;已知三角形的兩邊和其中一邊的對角,由於該三角形具有不穩定性,所以其解不確定,可結合平面幾何作圖的方法及“大邊對大角,大角對大邊”定理和三角形內角和定理去考慮解決問題
(3)相關結論:
a/sinA=b/sinB=c/sinC=(a+b)/(sinA+sinB)=(a+b+c)/(sinA+sinB+sinC)
c/sinC=c/sinD=BD=2R
⑷設R為三角外接圓半徑,公式可擴展為:a/sinA=b/sinB=c/sinC=2R,即當一內角為90°時,所對的邊為外接圓的直徑。靈活運用正弦定理,還需要知道它的幾個變形
sinA=a/2R,sinB=b/2R,sinC=c/2R
asinB=bsinA,bsinC=csinB,asinC=csinA