正弦定律

正弦定律，是指設三角形的三邊為a b c，他們的對角分別為A B C，外接圓半徑為r，則稱關係式a/sinA=b/sinB=c/sinC=2r為正弦定理。

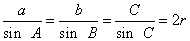
證明
步驟1.
在銳角△ABC中，設三邊為a，b，c。作Ch⊥AB垂足為點D
CH=a·sinB
CH=b·sinA
∴a·sinB=b·sinA
得到
a/sinA=b/sinB
同理，在△ABC中，
b/sinB=c/sinC
步驟2.
證明a/sinA=b/sinB=c/sinC=2R：
如圖，任意三角形ABC,作ABC的外接圓O.
作直徑BD交⊙O於D.
連線DA.
因為直徑所對的圓周角是直角,所以∠DAB=90度
因為同弧所對的圓周角相等,所以∠D等於∠C.
所以c/sinC＝c/sinD=BD=2R
a/SinA=BC/SinD=BD=2R
類似可證其餘兩個等式。
二. 正弦定理的變形公式
(1) a=2RsinA, b=2RsinB, c=2RsinC;
(2) sinA : sinB : sinC = a : b : c;