概念
初等函式是由冪函式(powerfunction)、指數函式(exponentialfunction)、對數函式(logarithmicfunction)、三角函式(trigonometricfunction)、反三角函式(inversetrigonometicfunction)與常數經過有限次的有理運算(加、減、乘、除、有理數次乘方、有理數次開方)及有限次函式複合所產生、並且能用一個解析式表示的函式。
它是最常用的一類函式,包括常數函式、冪函式、指數函式、對數函式、三角函式、反三角函式(以上是基本初等函式),以及由這些函式經過有限次四則運算或函式的複合而得的所有函式。即基本初等函式經過有限次的四則運算或有限次的函式複合所構成並可以用一個解釋式表出的函式,稱為初等函式。
還有一系列雙曲函式也是初等函式,如sinh的名稱是雙曲線正弦或超正弦,cosh是雙曲餘弦或超餘弦,tanh是雙曲線正切、coth是雙曲線餘切、sech是雙曲線正割、csch是雙曲線餘割。初等函式在其定義區間內連續。
實例介紹
常值函式
對定義域中的一切x對應的函式值都取某個固定常數的函式。
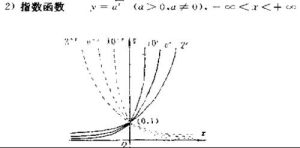 指數函式
指數函式冪函式
形如y=x^a的函式,式中a為實常數。
指數函式
形如y=a^x的函式,式中a為不等於1的正常數。
 基本函式
基本函式對數函式
指數函式的反函式,記作y=logaax,式中a為不等於1的正常數,定義域是X〉0。指數函式與對數函式之間成立關係式,logaax=x。
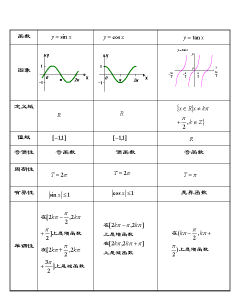
三角函式
即正弦函式y=sinx,餘弦函式y=cosx,正切函式y=tanx,餘切函式y=cotx,正割函式y=secx,餘割函式y=cscx(見三角學)。
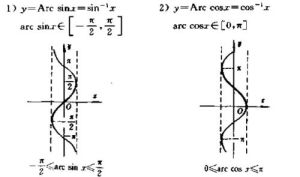
反三角函式
三角函式的反函式——反正弦函式y=arcsinx,反餘弦函式y=arccosx(-1≤x≤1,0≤y≤π),反正切函式y=arctanx,反餘切函式y=arccotx(-∞<+∞,θ<π等="等"以上這些函式常統稱為基本初等函式="以上這些函式常統稱為基本初等函式">
雙曲正弦或超正弦sinhx=(e^x-e^(-x))/2
雙曲餘弦或超餘弦coshx=(e^x+e^(-x))/2
雙曲正切tanhx=sinhx/coshx
雙曲餘切cothx=1/tanhx
雙曲正割sechx=1/coshx
雙曲餘割cschx=1/sinhx
一個初等函式,除了可以用初等解析式表示以外,往往還有其他表示形式,例如,三角函式y=sinx可以用無窮級數表為初等函式可以按照解析表達式分類為:初等函式是最先被研究的一類函式,它與人類的生產和生活密切相關,並且套用廣泛。為了方便,人們編制了各種函式表,如平方表、開方表、對數表、三角函式表等。