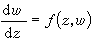常微分方程解析理論
正文
復域上的常微分方程理論;套用複變函數論研究微分方程的性狀,以及把微分方程的解視為由方程定義的解析函式,並直接從微分方程本身研究解的性質的理論。這是基於A.-L.柯西的基本定理,即在對微分方程作極為廣泛的假設下,它的積分是復變數的解析函式。常微分方程解析理論與複變函數理論的發展密切相關。它的先驅性工作是由柯西、(G.F.)B.黎曼、I.L.富克斯、(J.-)H.龐加萊以及P.班勒衛等人所作。解的存在性和惟一性定理 微分方程理論中最基本的問題是已給的方程是否有解,早先的數學家們力圖通過已知初等函式的有限組合來表示微分方程的解,但在這個觀念下大多數微分方程不可積。這實際上是要求方程的大範圍通解,是不合適的,因為典型的分析運算與極限過程只要求局部的觀點。另一方面,在物理和力學中的問題常是只要求適合某些補充條件的特解。於是柯西提出考慮如下的問題:方程
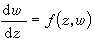 (1)
(1)
奇點 柯西存在性定理所證明的微分方程的解是局部的。即給出了一個解析函式元素,套用外爾斯特拉斯的解析開拓(見常微分方程初值問題)的方法,從z0點的鄰域沿一途徑Г開拓這個函式元素,如果方程(1)的右端也能沿Γ開拓,則解的開拓元素也滿足方程。如果沿著所有可能的途徑進行開拓,則得到的所有函式元素構成的集合在大範圍定義了一個單值的或多值的函式。現在重要的問題是在解的整個存在區域上來研究它,而解的存在區域和解的性質是由它的奇點所決定的,這裡奇點是指柯西存在性定理不成立的那些點。因此需要研究所考慮的方程的解的奇點的位置和性質。
微分方程的解出現的奇點較解析函式論中的情況要複雜得多。首先當自變數圍繞某些點轉一圈以後,函式從一個值變為另一個值,稱這些點為分支點。代數函式可能具有的奇點稱為代數奇點。非代數奇點的分類基於不定區的概念,函式ƒ在z0點的不定區是指以z0為中心的小圓在ƒ映射下的像集合當圓半徑趨於0時的極根集合。若點z0的不定區由一點組成,則稱z0為超越奇點,否則稱為本性奇點。富克斯還對微分方程解的奇點提出一種重要的區分,即分為固定奇點和流動奇點。前一種由微分方程本身給出其位置和性質,與方程的個別解無關,也即與通解中所含的任意常數無關。後者則依賴於柯西問題的初始值,也就是依賴於特解的選擇,它與任意常數一起變動。例如方程
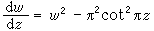 的解以整數和無窮遠點為固定奇點(極點);
的解以整數和無窮遠點為固定奇點(極點);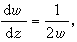
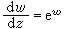 和
和 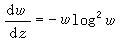 分別有解為
分別有解為 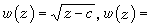
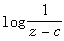 和
和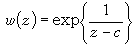 此時с分別是流動代數分支點,流動對數分支點和流動本性奇點。
此時с分別是流動代數分支點,流動對數分支點和流動本性奇點。 班勒衛曾證明如下的定理(稱班勒衛定理):若z0是方程(1)的解的奇點,則(z0,w0)不是方程右端ƒ(z,w)的全純點。
這個定理首次確定解的奇點和方程奇點的關係,同時還說明在方程右端 ƒ(z, w)的全純點處除了全純解之外,不存在非全純的解。當方程右端是w 的有理函式時,班勒曾衛列舉可能出現奇點的種種情況。此外,如果ƒ(z,w)=P(z,w)/Q(z,w),(z0,w0)是P(z,w)和Q(z,w)的全純點, 但P(z0,w0)=Q(z0,z0)=0,這種不確定的情形下,即使在P(z,w)和Q(z,w)是z 和w 的線性函式的情形,其解在z0點的鄰域的性質也相當複雜。
一般地,當對方程的性狀加上某些限制以後,也帶給解的奇點某些限制,例如線性微分方程的解無流動奇點。1887年班勒衛曾證明,未知函式及其導數代數地出現於方程,而係數是z的解析函式的一階代數微分方程,它的解無流動超越奇點和流動本性奇點。
反過來,如果對解的奇點作某些限制時,微分方程也要適合某些條件,例如其解無任何奇點的方程必為
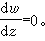 一個重要的結論是:如果方程(1)的右端是w 的有理函式,其解無流動代數分支點,則方程(1)必化為如下的黎卡提方程
一個重要的結論是:如果方程(1)的右端是w 的有理函式,其解無流動代數分支點,則方程(1)必化為如下的黎卡提方程 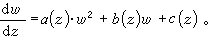 (2)
(2)
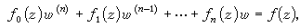
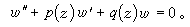 (3)
(3)
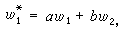
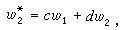 令λ1和λ2是A=
令λ1和λ2是A=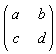 的特徵根,則當λ1≠λ2時,(3)的解能寫為
的特徵根,則當λ1≠λ2時,(3)的解能寫為 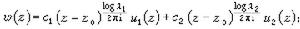
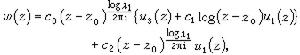
下述幾個特殊的二階線性方程在實際套用和理論中都很重要。
富克斯方程 它是奇點全為正則奇點的方程。由於z0為正則奇點的充分必要條件是(z-z0)p(z)和(z-z0)2q(z)在z0點領域全純,因此富克斯方程可寫為
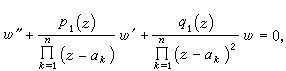 (4)
(4)
img src="image/67-7.gif" align="absmiddle"> (5)
為在αk點的指標方程,其中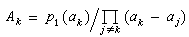 ,
,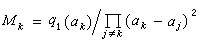 。方程(5)的根稱為指標數,記為
。方程(5)的根稱為指標數,記為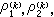 且有著名的富克斯關係式
且有著名的富克斯關係式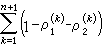
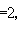 這裡αn+1=
這裡αn+1= 。如果奇點的個數<4且都位於有限平面內,則方程能由奇點的位置和相應的指標數完全確定。特別是當 n=3時即導出超幾何方程。對這個方程的研究有著悠久的歷史,許多傑出的數學家如L.歐拉、C.F.高斯、E.E.庫默爾和黎曼等人都有重要的貢獻。這類方程在很多情形中出現,它與共形映射、差分方程、連分數和自守函式都有關係;且其理論具有形式上的高度完美性,今設 αk(k=1,2,3)為奇點,(
。如果奇點的個數<4且都位於有限平面內,則方程能由奇點的位置和相應的指標數完全確定。特別是當 n=3時即導出超幾何方程。對這個方程的研究有著悠久的歷史,許多傑出的數學家如L.歐拉、C.F.高斯、E.E.庫默爾和黎曼等人都有重要的貢獻。這類方程在很多情形中出現,它與共形映射、差分方程、連分數和自守函式都有關係;且其理論具有形式上的高度完美性,今設 αk(k=1,2,3)為奇點,(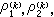 )為相應的指標數,則方程可寫為
)為相應的指標數,則方程可寫為 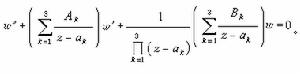
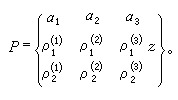
若富克斯方程的奇點為0、1和
 ,則引入超幾何函式中常用的參數之後能導出高斯的標準形式
,則引入超幾何函式中常用的參數之後能導出高斯的標準形式 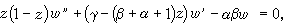
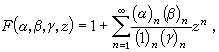
勒讓德方程 它是形如
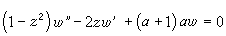
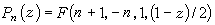 。
。
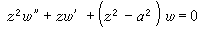
施瓦茲方程 它是與二階線性微分方程緊密相關的一類方程, 它由共形地映w上半平面為z平面上圓弧多邊形內部的函式所滿足,方程為
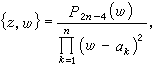 (6)
(6)
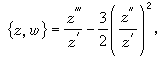 稱為施瓦茲導數;α1,α2,…,αn為多邊形的角點, P2n-4(w)和2n-4次多項式。方程(6)的解具有一個重要的性質,即當圍繞奇點環行一周時,它接受一個分式線性變換
稱為施瓦茲導數;α1,α2,…,αn為多邊形的角點, P2n-4(w)和2n-4次多項式。方程(6)的解具有一個重要的性質,即當圍繞奇點環行一周時,它接受一個分式線性變換 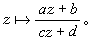 又知二階線性方程的兩個線性獨立的解之比亦具有相同的性質,因此方程(6) 的求解問題能化為適當選取的二階線性方程的求解。設G是一分式線性變換群,ƒ(z)為一單值亞純函式,如對於任一g∈G有ƒ(g(z))=ƒ(z),則稱ƒ(z)是關於群 G的自守函式。自守函式與二階微分方程有下述的關係:設w=ƒ(z)為自守函式,則z作為w 的函式可用微分方程z″+uz=0的兩個獨立解z1(w)和z2(w)之商表示<即
又知二階線性方程的兩個線性獨立的解之比亦具有相同的性質,因此方程(6) 的求解問題能化為適當選取的二階線性方程的求解。設G是一分式線性變換群,ƒ(z)為一單值亞純函式,如對於任一g∈G有ƒ(g(z))=ƒ(z),則稱ƒ(z)是關於群 G的自守函式。自守函式與二階微分方程有下述的關係:設w=ƒ(z)為自守函式,則z作為w 的函式可用微分方程z″+uz=0的兩個獨立解z1(w)和z2(w)之商表示<即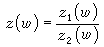 的反函式為w=ƒ(z)。
的反函式為w=ƒ(z)。 非線性微分方程 由於許多物理系統是非線性的,從而描述它們的微分方程也是非線性的,即未知函式或其導數非線性地出現於方程之中。對於非線性方程一般性質的了解不像線性方程那樣完備和深入,而是知道得很少,而且它具有線性方程理論中所未見的新現象。下面只敘述非線性方程理論中的一些事實。
1856年C.A.布里奧和J.-C.布凱考慮如下的方程
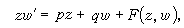 (7)
(7)
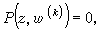 (8)
(8)
19世紀末,班勒衛首先討論了方程
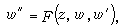 式中F(z,w,w┡)是w和w┡的有理函式,係數為z的解析函式。他考慮定出只具有固定分支點和本性奇點的方程。B.O.岡比埃和富克斯對此問題亦作出重要貢獻。一般方法是由班勒衛提出,基本技巧是他的α-方法。他們找到了50個不同的類型,但大多數能化為已知的方程,如線性方程或黎卡提方程。只有 6種類型的方程導出新的超越亞純函式,這些方程是:
式中F(z,w,w┡)是w和w┡的有理函式,係數為z的解析函式。他考慮定出只具有固定分支點和本性奇點的方程。B.O.岡比埃和富克斯對此問題亦作出重要貢獻。一般方法是由班勒衛提出,基本技巧是他的α-方法。他們找到了50個不同的類型,但大多數能化為已知的方程,如線性方程或黎卡提方程。只有 6種類型的方程導出新的超越亞純函式,這些方程是: 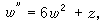
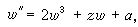
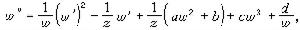
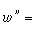
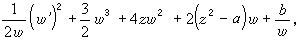 等等,並稱這些方程為班勒衛方程,它們的解稱為班勒衛函式。1913~1914年,P.L.布特魯對一類二階方程發展了漸近積分的方法,並指出班勒衛方程的解在某種意義下漸近於外爾斯特拉斯橢圓函式。
等等,並稱這些方程為班勒衛方程,它們的解稱為班勒衛函式。1913~1914年,P.L.布特魯對一類二階方程發展了漸近積分的方法,並指出班勒衛方程的解在某種意義下漸近於外爾斯特拉斯橢圓函式。 常微分方程理論中奈望林納理論的套用 20世紀20年代芬蘭數學家R.奈望林納創立了亞純函式值分布理論。不久日本數學家吉田耕作套用此理論於一類非線性常微分方程的研究。50年代H.維蒂希更系統地研究了奈望林納理論對常微分方程理論的意義,使得這一理論成為研究一類方程解的某些大範圍性質(解的增長性,值分布性質,因子分解等)的重要工具。作為柯西存在惟一性定理的直接推論是下述常係數微分方程
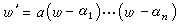 (9)
(9)
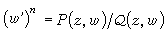 (10)
(10)
上述類型的定理有種種證明和推廣,其中一個重要的補充是由N.施泰因梅茨所得,他證明了:若(10)存在超越亞純解, 則經過適當的分式線性變換
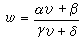 能化為6類標準的方程之一或它們的冪。這些方程除黎卡提方程外是:
能化為6類標準的方程之一或它們的冪。這些方程除黎卡提方程外是: 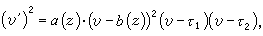
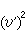
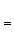
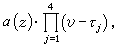
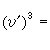
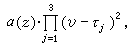
此外,對於代數微分方程亦有相應的結果,中國數學工作者對相當廣泛的高階代數微分方程存在“較快”增長的代數體函式解的必要條件亦得到精確形式的馬爾姆奎斯特型定理。近年來奈望林納理論還被用來研究常微分方程復振盪理論、解的增長性估計和解的因子分解等。