定義
 增函式
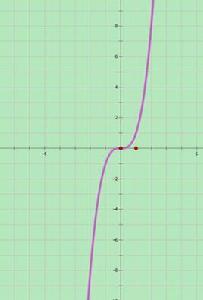
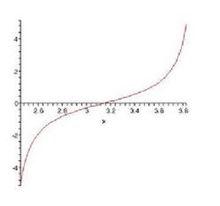
增函式一般地,設函式f(x)的定義域為D,如果對於定義域D內的某個區間上的任意兩個自變數的值x1,x2,當x1<x2時,都有f(x1)<f(x2),那么就說f(x)在這個區間上是增函式。 此區間就叫做函式f(x)的單調增區間。
隨著X增大,Y增大者為增函式。
遞推
增函式+增函式=增函式
減函式+減函式=減函式
增函式-減函式=增函式
減函式-增函式=減函式
增函式-增函式=不能確定
減函式-減函式=不能確定
判斷增、減函式常用的幾種方法
判斷函式單調性的基本方法有:
①定義法
②圖像法
③複合函式法
④導數法等等。
而定義法和導數法是做題中最常用的兩種方法。
定義法
根據定義,我們可以歸納出用定義法證明函式單調性的思路為:
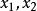 增函式
增函式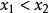 增函式
增函式1)取值:設為該相應區間的任意兩個值,並規定它們的大小,如;
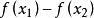 增函式
增函式2)作差:計算,並通過因式分解、配方、有理化等方法作有利於判斷其符號的變形;
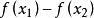 增函式
增函式3)定號:判斷的符號,若不能確定,則可分區間討論;
4)結論:根據差的符號,得出單調性的結論。
導數法
 增函式
增函式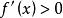 增函式
增函式 增函式
增函式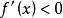 增函式
增函式 增函式
增函式一般地,對於給定區間上的函式,如果,那么就說在這個區間上是增函式;如果,那么就說在這個區間上是減函式。
我們也可以歸納出用導數法證明函式單調性的基本思路:
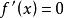 增函式
增函式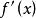 增函式
增函式 增函式
增函式一般應先確定函式的定義域,再求導數,通過判斷函式定義域被導數為零的點()所劃分的各區間內的符號來確定函式在該區間上的單調性。