![整數[數學名稱]](/img/b/542/nBnauM3X2UTM0ADO2EzMyAjMyQTM5YzN4MDMyQTNwAzMwIzLxMzLzczLt92YucmbvRWdo5Cd0FmLzE2LvoDc0RHa.jpg "整數[數學名稱]")
關於整數集
為什麼用Z表示整數集呢？這個涉及到一個德國女數學家對環理論的貢獻，她叫諾特。
1920年，她已引入“左模”，“右模”的概念。1921年寫出的《整環的理想理論》是交換代數發展的里程碑。其中，諾特在引入整數環概念的時候（整數集本身也是一個數環），她是德國人，德語中的整數叫做Zahlen，於是當時她將整數環記作Z，從那時候起整數集就用Z表示了。
數學分類
整數的分類
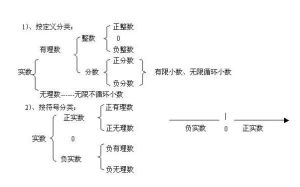整數1.正整數，即大於0的整數如，1，2，3······直到n。
2.既不是正整數，也不是負整數，它是介於正整數和負整數的數。
3.負整數，即小於0的整數如，-1，-2，-3······直到-n。
正整數
它是從古代以來人類計數的工具。可以說，從“一頭牛，兩頭牛”或是“五個人，六個人”抽象化成正整數的過程是相當自然的。正整數也可分成奇數和偶數兩類
零
不僅表示“沒有”（“無”），更是表示空位的符號。中國古代用算籌計算數並進行運算時，空位不放算籌，雖無空位記號，但仍能為位值記數與四則運算創造良好的條件。印度-阿拉伯命數法中的零(Zero)來自印度的(Sunya)字，其原意也是“空”或“空白”。負整數
中國最早引進了負數。《九章算術.方程》中論述的“正負數”，就是整數的加減法。減法的需要也促進了負整數的引入。減法運算可看作求解方程a-b=c，如果a、b是自然數，則所給方程未必有自然數解。為了使它恆有解，就有必要把自然數系擴大為整數系。奇數
在整數中，不能被2整除的數叫做奇數。日常生活中，人們通常把奇數叫做單數，它跟偶數是相對的。偶數
整數中，能夠被2整除的數，叫做偶數，又稱雙數。偶數包括正偶數、負偶數和0。
所有整數不是奇數（又稱單數），就是偶數。當n是整數時，偶數可表示為2n（n為整數）；奇數則可表示為2n+1（或2n-1）。在十進制里，我們可用看個位數的方式判斷該數是奇數還是偶數：個位為1,3,5,7,9的數為奇數；個位為0,2,4,6,8的數為偶數。
備註：現中學數學教材中規定：零和正整數為自然數。
代數性質
下表給出任何整數a，b和c的加法和乘法的基本性質。| 性質 | 加法 | 乘法 |
| 封閉性 | a+b是整數 | a×b是整數 |
| 結合律 | a+(b+c)=(a+b)+c是整數 | a×(b×c)=(a×b)×c是整數 |
| 交換律 | a+b=b+a | a×b=b×a |
| 存在單位元 | a+0=a | a×1=a |
| 存在逆元 | a+（-a）=0 | 在整數集中，只有1或-1關於乘法存在整數逆元 |
| 分配律 | a×(b+c)=a×b+a×c |
性質套用
如果不加特殊說明，我們所涉及的數都是整數，所採用的字母也表示整數。定義
設a,b是給定的數，b≠0，若存在整數c，使得a=bc,則稱b整除a，記作b|a，並稱b是a的一個約數(因子)，稱a是b的一個倍數，如果不存在上述c，則稱b不能整除a。整數整除性的一些數碼特徵（即常見結論）
1與0的特性
1是任何整數的約數，即對於任何整數a，總有1|a。0是任何非零整數的倍數，a≠0,a為整數，則a|0。
整除特徵
（1）若一個整數的末位是0、2、4、6或8，則這個數能被2整除。（2）若一個整數的數字和能被3整除，則這個整數能被3整除。
（3）若一個整數的末尾兩位數能被4整除，則這個數能被4整除。
（4）若一個整數的末位是0或5，則這個數能被5整除。
（5）若一個整數能被2和3整除，則這個數能被6整除。
（6）若一個整數的個位數字截去，再從餘下的數中，減去個位數的2倍，如果差是7的倍數，則原數能被7整除。如果差太大或心算不易看出是否7的倍數，就需要繼續上述「截尾、倍大、相減、驗差」的過程，直到能清楚判斷為止。例如，判斷133是否7的倍數的過程如下：13－3×2=7，所以133是7的倍數；又例如判斷6139是否7的倍數的過程如下：613－9×2=595，59－5×2=49，所以6139是7的倍數，余類推。
（7）若一個整數的未尾三位數能被8整除，則這個數能被8整除。
（8）若一個整數的數字和能被9整除，則這個整數能被9整除。
（9）若一個整數的末位是0，則這個數能被10整除。
（10）若一個整數的奇位數字之和與偶位數字之和的差能被11整除，則這個數能被11整除。11的倍數檢驗法也可用上述檢查7的「割尾法」處理。過程唯一不同的是：倍數不是2而是1。
（11）若一個整數能被3和4整除，則這個數能被12整除。
（12）若一個整數的個位數字截去，再從餘下的數中，加上個位數的4倍，如果差是13的倍數，則原數能被13整除。如果差太大或心算不易看出是否13的倍數，就需要繼續上述「截尾、倍大、相加、驗差」的過程，直到能清楚判斷為止。
（13）若一個整數的個位數字截去，再從餘下的數中，減去個位數的5倍，如果差是17的倍數，則原數能被17整除。如果差太大或心算不易看出是否17的倍數，就需要繼續上述「截尾、倍大、相減、驗差」的過程，直到能清楚判斷為止。
（14）若一個整數的個位數字截去，再從餘下的數中，加上個位數的2倍，如果差是19的倍數，則原數能被19整除。如果差太大或心算不易看出是否19的倍數，就需要繼續上述「截尾、倍大、相加、驗差」的過程，直到能清楚判斷為止。
（15）若一個整數的末三位與3倍的前面的隔出數的差能被17整除，則這個數能被17整除。
（16）若一個整數的末三位與7倍的前面的隔出數的差能被19整除，則這個數能被19整除。
（17）若一個整數的末四位與前面5倍的隔出數的差能被23(或29)整除，則這個數能被23整除
奇偶性
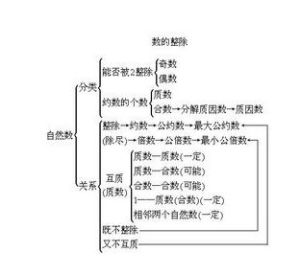整數2、奇數的平方都可以表示成(8m+1)的形式，偶數的平方可以表示為8m或（8m+4)的形式；
3、若有限個整數之積為奇數，則其中每個整數都是奇數；若有限個整數之積為偶數，則這些整數中至少有一個是偶數；兩個整數的和與差具有相同的奇偶性；偶數的平方根若是整數，它必偶數。
完全平方數
能表示為某整數的平方的數稱為完全平方數，簡稱平方數。平方數有以下性質與結論：
（1）平方數的個位數字只可能是0,1，4,5，6,9；
（2）偶數的平方數是4的倍數，奇數的平方數被8除餘1，即任何平方數被4除的餘數只有可能是0或1；
（3）奇數平方的十位數字是偶數；
（4）十位數字是奇數的平方數的個位數一定是6；
（5）不能被3整除的數的平方被3除餘1，能被3整除的數的平方能被3整除。因而，平方數被9也合乎的餘數為0,1，4,7，且此平方數的各位數字的和被9除的餘數也只能是0,1，4,7；
（6）平方數的約數的個數為奇數；
（7）任何四個連續整數的乘積加1，必定是一個平方數。
（8）設正整數a,b之積是一個正整數的k次方冪（k≥2），若（a,b）=1，則a,b都是整數的k次方冪。一般地，設正整數a,b,c……之積是一個正整數的k次方冪（k≥2），若a,b,c……兩兩互素，則a,b,c……都是正整數的k次方冪。
JAVA語言
integer是對象，用一個引用指向這個對象。
Java中的數據類型分為基本數據類型和複雜數據類型int是前者>>integer是後者（也就是一個類）
