定義
定義一:在整數中,能被2整除的數,叫做偶數。
定義二:二的倍數叫做偶數。
在十進制里,可以看個位數判定該數是奇數(單數)還是偶數(雙數):個位為1,3,5,7,9的數是奇數(單數);個位為0,2,4,6,8的數是偶數(雙數)。
哥德巴赫猜想說明任何大於二的偶數(雙數)都可以寫為兩個質數之和,但尚未有人能證明這個猜想。
在中國文化里,偶有一雙一對、團圓的意思。古時認為偶數(雙數)好,奇數(單數)不好;所以運氣不好叫做“不偶”。
零的介紹
0是一個特殊的偶數。它既是正偶數與負偶數的分界線,又是正奇數與負奇數的分水嶺。
性質
關於偶數和奇數,有下面的性質:
(1)兩個連續整數中必是一個奇數一個偶數;
(2)奇數與奇數的和或差是偶數;偶數與奇數的和或差是奇數;任意多個偶數的和都是偶數;單數個奇數的和是奇數;雙數個奇數的和是偶數;
(3)兩個奇(偶)數的和或差是偶數;一個偶數與一個奇數的和或差一定是奇數;
(4)除2外所有的正偶數均為合數;
(5)相鄰偶數最大公約數為2,最低公倍數為它們乘積的一半;
(6)奇數與奇數的積是奇數;偶數與偶數的積是偶數;奇數與偶數的積是偶數;
(7) 偶數的個位一定是0、2、4、6或8;奇數的個位一定是1、3、5、7或9;
(8)任何一個奇數都不等於任何一個偶數;若干個整數的連乘積,如果其中有一個偶數,乘積必然是偶數;
(9)偶數的平方被4整除,奇數的平方被8除餘1。
上述性質可通過對奇數和偶數的代數式進行相應運算得出。
如證明:兩個奇數的和為偶數.
 偶數
偶數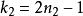 偶數
偶數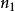 偶數
偶數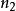 偶數
偶數可令兩奇數;(其中,皆為整數)。
 偶數
偶數則,
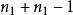 偶數
偶數由於括弧內的多項式是整數,從而原命題得證。
偶數列
 偶數
偶數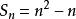 偶數
偶數數列0,2,4,6,8,……,2(n-1)稱為偶數列。偶數列的通項公式:;偶數列前n項的和:。偶數列實質上是一個等差數列,首項為0,公差為2。