偶函式

在數學裡，偶函式和奇函式是滿足著相對於加法逆元之特定對稱關係的函式。這在數學分析的許多領域中都很重要，特別是在冪級數和傅立葉級數的理論里。其命名是因為冪函式的冪的奇偶性滿足下列條件：若n為一偶數，則函式xn是偶函式，若n為一奇數，則為奇函式。設f(x)為一實變數實值函式，則f為偶函式若下列的方程對所有實數x都成立：f(x) = f(-x)。幾何上，一個偶函式會對y軸對稱，亦即其圖在對y軸為鏡射後不會改變。偶函式的例子有|x|、x2、x4、cos(x)和cosh(sec)(x)。偶函式不可能是個雙射映射。

基本信息

• 中文名：偶函式
• 英文名：Even function

• 形式：f(x)=f(-x)
• 特性：定義域必須關於y軸對稱

概述

偶函式

1、如果知道函式表達式,對於函式f(x)的定義域內任意一個x，都滿足 f(x)=f(-x) 如y=x²，y=cos x
2、如果知道圖像,偶函式圖像關於y軸（直線x=0）對稱。
3、偶函式的定義域D關於原點對稱是這個函式成為偶函式的必要非充分條件.
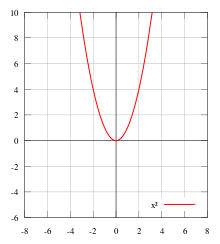
例如:f(x)=x^2，x∈R(f(x)等於x的平方，x屬於一切實數)，此時的f(x)為偶函
數.f(x)=x^2，x∈(-2,2](f(x)等於x的平方，-2
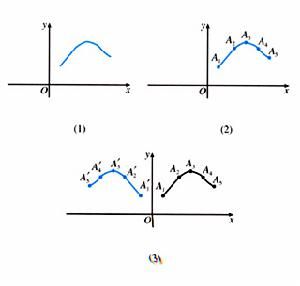
如圖①奇函式（關於原點對稱），圖②即為偶函式，（關於y軸對稱）
注意 定義域為關於y軸對稱，則f(x)=f(-x)一定是是偶函式
相關函式：奇函式，非奇非偶函式
定義：1、如果知道函式表達式，滿足f(x)=f(-x) 如y=x*x，y=Cosx 2、如果知道圖像，偶函式圖像關於y軸（x=0）對稱
3、偶函式的定義域必須關於原點對稱，否則不能成為偶函式
如圖（1）奇函式（關於原點對稱），圖(2)偶函式，（關於y軸對稱）

判斷方法

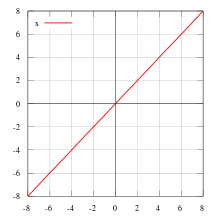f(x) = x，奇函式的一個例子

先判斷定義域是否關於原點和Y軸對稱，若不對稱，即為非奇非偶，若對稱，f(-x)=-f(x)的是奇函式 f(-x)=f(x)的是偶函式
幾何判斷方法：
關於原點對稱的函式是奇函式，關於Y軸對稱的函式是偶函式
如果f(x)為偶函式，則f(x+a)=f(-x-a)

運算方法

(1) 兩個偶函式相加所得的和為偶函式.
(2) 兩個奇函式相加所得的和為奇函式.
(3) 一個偶函式與一個奇函式相加所得的和為非奇函式與非偶函式.
(4) 兩個偶函式相乘所得的積為偶函式.
(5) 兩個奇函式相乘所得的積為偶函式.
(6) 一個偶函式與一個奇函式相乘所得的積為奇函式.
(7)奇函式一定滿足f(0)=0（因為F（0）這個表達式表示0在定義域範圍內，0在定義域範圍內，F(0)就必須為0）所以奇函式不一定有f(0)，但有F（0）時F（0）必須等於0，不一定有f(0)=0，推出奇函式，此時函式不一定為奇函式，例f(x)=x^2.
（8）定義在R上的奇函式f（x）必滿足f（0）=0；
——因為定義在R上，所以在x=0點存在f(0)，要想關於原點對稱，在原點又只能取一個y值，只能是f(0)=0。
（這是一條可以直接拿來用的結論：當x可以取0，f（x）又是奇函式時，f（0）=0）。
（9）若且唯若f（x）=0（定義域關於原點對稱）時，f（x）既是奇函式又是偶函式。
(10) 在對稱區間上，被積函式為奇函式的定積分為零。