信息率-失真理論
正文
研究在限定失真下為了恢覆信源符號所必需的信息率,簡稱率失真理論。信源發出的符號傳到信宿後,一般不能完全保持原樣,而會產生失真。要避免這種失真幾乎是不可能,而且也無必要,因為信宿不管是人還是機器,靈敏度總是有限的,不可能覺察無窮微小的失真。倘若在處理信源符號時允許一定限度的失真,可減小所必需的信息率,有利於傳輸和存儲。率失真理論就是用以計算不同類型的信源在各種失真限度下所需的最小信息率。因此,這一理論是現代所有信息處理問題的理論基礎。在50年代,資訊理論主要研究無失真的信息傳輸問題。信源編碼著眼於無失真地恢覆信源符號的最小信息率。1959年,C.E.仙農發表《逼真度準則下的離散信源編碼定理》一文,提出了率失真函數的概念,逐漸形成率失真理論並不斷得到完善。這一理論能解決許多類型的信源問題,並擴大到多用戶相關信源問題。
率失真函式 計算率失真函式是率失真理論的中心問題。要定義率失真函式,必須先定量地表達失真的程度,因此需要規定失真函式d(u,v)。u是信源符號U的樣,u∈A,A是信源集,可以是連續的實數區間,也可以是離散的有限集如A={ɑ1,ɑ2,…,ɑn}。v 是信宿得到的符號V 的樣,v∈B,B可以等於A也可以不同。因此失真函式d 是一個二元函式。當用v代替u不引起失真時,可使d(u,v)=0,若引起失真,就按失真程度規定d(u,v)為正實數集內的一個數。由於U 和V 都是隨機量,d(u,v)也將是隨機量,因此還須定義平均失真
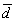 作為失真的度量,即
作為失真的度量,即 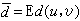
當信源和信宿是隨機序列U1,U2,…,UN和V1,V2,…,VN時,可定義平均失真為
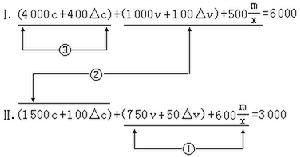
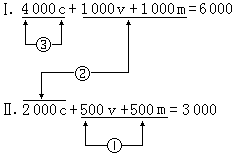
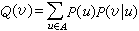
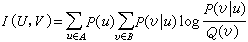

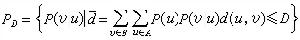
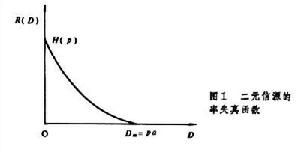
當信源機率P(u)已知,失真函式d(u,v)已規定時,可用求極值法來計算R(D)函式。實際計算一般相當複雜,有時尚須藉助於計算機作疊代運算。最常見的二元信宿在對稱失真函式時,率失真函式(圖1)是
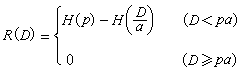
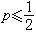 ,失真函式是
,失真函式是 d(0,0)=d(1,1)=0d(0,1)=d(1,0)=ɑ
H 是熵函式,即H(z)=-zlogz-(1-z)log(1-z)(0≤z≤1)
正態信源在均方失真的規定下,率失真函式是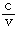
 信息率-失真理論
信息率-失真理論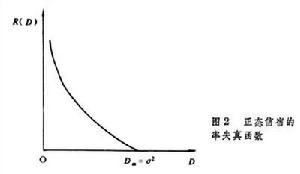 信息率-失真理論
信息率-失真理論限失真信源編碼定理 率失真函式只指出限失真條件下所必需的最小信息率。從理論上講,尚應能證明實際存在一種編碼方法,用這樣的信息率就能實現限失真的要求。這就是限失真信源編碼定理。這個定理可表述為:只要信源符號序列長度N足夠大,當每個符號的信息率大於R(D),必存在一種編碼方法,其平均失真可無限逼近D;反之,若信息率小於R(D),則任何編碼的平均失真必將大於D。
對於無記憶平穩離散信源,上述定理已被嚴格證明,並知其逼近誤差是依指數關係 e
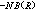 而衰減的。其中B(R)是信息率R的函式,當R>R(D)時,B(R)是正值,且隨R的增大而增大。因此當序列長度N增大時,誤差將趨於零。對於其他信源,結果還不十分完善。
而衰減的。其中B(R)是信息率R的函式,當R>R(D)時,B(R)是正值,且隨R的增大而增大。因此當序列長度N增大時,誤差將趨於零。對於其他信源,結果還不十分完善。 參考書目
T.Berger, Rate Distortion Theory,Prentice Hall, Engle wood Cliffs,New Jersey,1971.
